
§8-4稳恒磁场的高斯定理与安培环路定理 一、稳恒磁场的高斯定理 由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。 B.d5-0 高斯定理的积 分形式 穿过任意闭合曲面S的总磁通必然为零,这就 是稳恒磁场的高斯定理。 让美下元返回:退欢
上页 下页 返回 退出 穿过任意闭合曲面S的总磁通必然为零,这就 是稳恒磁场的高斯定理。 一、稳恒磁场的高斯定理 由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。 高斯定理的积 分形式 §8-4 稳恒磁场的高斯定理与安培环路定理 d = 0 S B S

激发静电场的场源(电荷)是电场线的源头或 尾闾,所以静电场是属于发散式的场,可称作有源 场;而磁场的磁感线无头无尾,恒是闭合的,所以 磁场可称作无源场。 在静电场中,由于自然界有单独存在的正、负 电荷,因此通过一闭合曲面的电通量可以不为零, 这反映了静电场是有源场。而在磁场中,磁力线的 连续性表明,像正、负电荷那样的磁单极是不存在 的,磁场是无源场。 1913年英国物理学家狄拉克曾从理论上预言磁 单极子的存在,但至今未被观察到
上页 下页 返回 退出 在静电场中,由于自然界有单独存在的正、负 电荷,因此通过一闭合曲面的电通量可以不为零, 这反映了静电场是有源场。而在磁场中,磁力线的 连续性表明,像正、负电荷那样的磁单极是不存在 的,磁场是无源场。 1913年英国物理学家狄拉克曾从理论上预言磁 单极子的存在,但至今未被观察到。 激发静电场的场源(电荷)是电场线的源头或 尾闾,所以静电场是属于发散式的场,可称作有源 场;而磁场的磁感线无头无尾,恒是闭合的,所以 磁场可称作无源场
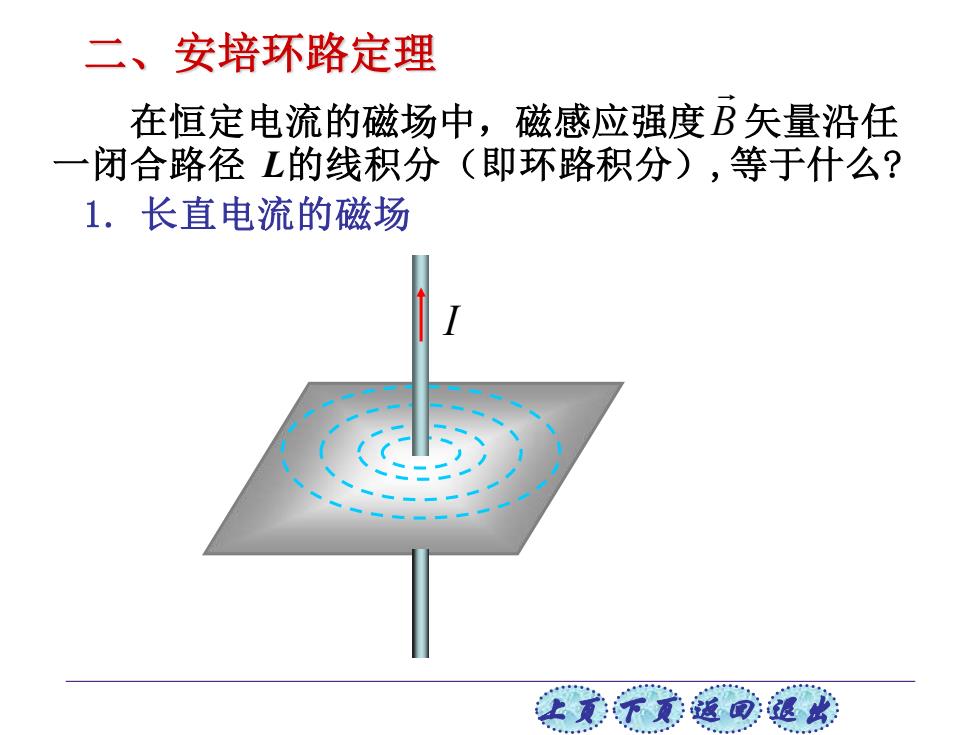
二、安培环路定理 在恒定电流的磁场中,磁感应强度B矢量沿任 一闭合路径L的线积分(即环路积分),等于什么? 1.长直电流的磁场 让美觉返司退
上页 下页 返回 退出 二、安培环路定理 1. 长直电流的磁场 I 在恒定电流的磁场中,磁感应强度 矢量沿任 一闭合路径 L的线积分(即环路积分),等于什么? B
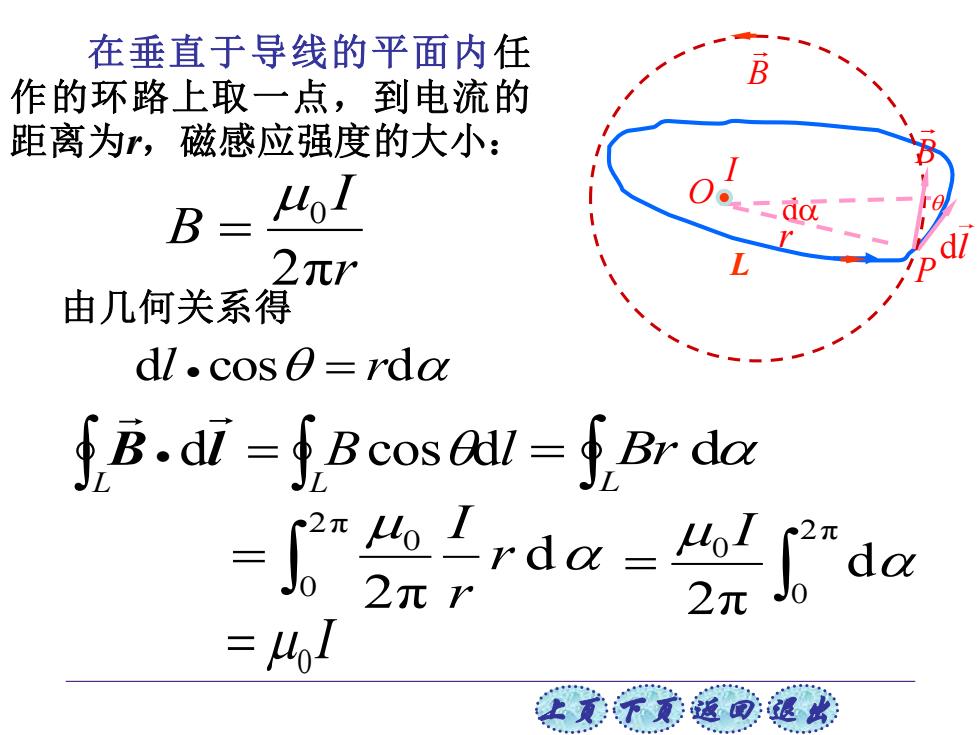
在垂直于导线的平面内任 作的环路上取一点,到电流的 距离为r,磁感应强度的大小: B= HoI 元r 由几何关系得 dl cos0 =rda fB.d=fBcosa=fBr da rdada 2元r 2元 =41 让意不意道可退欢
上页 下页 返回 退出 在垂直于导线的平面内任 作的环路上取一点,到电流的 距离为r,磁感应强度的大小: r I B 2π 0 = 由几何关系得 dl • cos = rd • = L L B dl Bcosdl = L Br d I = 0 d 2π 2π 0 0 r r I = L d dl = 2π 0 0 d 2π I O r P B B I

如果沿同一路径但改变绕 行方向积分: fB.d7=f Bcos(π-8)dl Bcosedi 2元 =-4。 结果为负值! 若认为电流为-【则结果可写为 f8.d=4(1) 让美下觉返同速
上页 下页 返回 退出 B l B l L L d cos(π )d • = − B l L = − cos d I = −0 d 2π 2π 0 0 = − I 如果沿同一路径但改变绕 行方向积分: 结果为负值! 若认为电流为-I 则结果可写为 L O r P B B I d dr B l ( I) L = − • 0 d

如果闭合曲线不在垂直于 导线的平面内: B.d=f B(d7+di) =fBcos90d出+fBcos6d出 =0+f Br da 2元r =4 结果一样! 让意不意适回退块
上页 下页 返回 退出 • = ⊥ + L L B dl B (dl dl )/ / d / / Bcos90 dl Bcos l L L = ⊥ + I = 0 = + L 0 Br d d 2π 2π 0 0 r r I = 如果闭合曲线不在垂直于 导线的平面内: 结果一样! I d // r ⊥ dr dr L
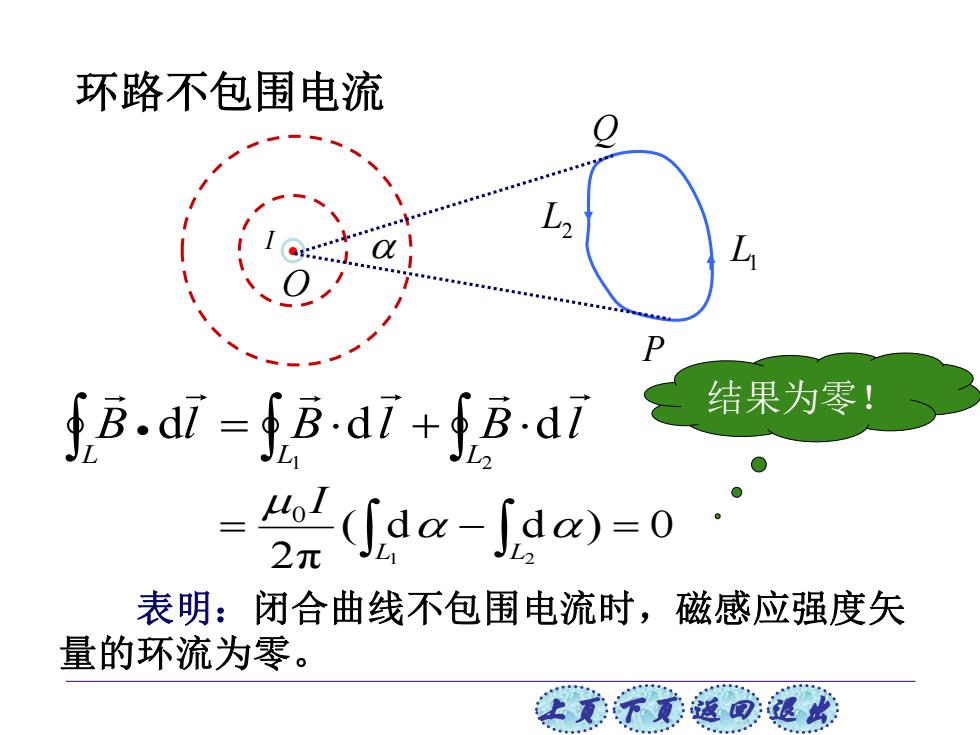
环路不包围电流 fB.d7=fB.d7+fB.d 结果为零! 2%aa-w)=0 表明:闭合曲线不包围电流时,磁感应强度矢 量的环流为零。 让美觉返司退
上页 下页 返回 退出 I B l B l B l L L L d d d 1 2 • = + ( d d ) 0 2π 1 2 0 = − = L L I 结果为零! 表明:闭合曲线不包围电流时,磁感应强度矢 量的环流为零。 环路不包围电流 O Q L2 P L1

上述结论虽是从长直载流导线磁场得来,却具普遍性 安培环路定理 在磁场中,沿任一闭合曲线B矢量的线积 分(也称B矢量的环流),等于真空中的磁导 率乘以穿过以这闭合曲线为边界所张任意曲 面的各恒定电流的代数和。 fB.di=4,∑1 为正值 电流的正负规定:积 绕行方向 分路径的绕行方向与电流 成右手螺旋关系时,电流1 为正值;反之为负值。 为负值 让贰子元道同退此
上页 下页 返回 退出 B l = I L d 0 安培环路定理 电流I的正负规定:积 分路径的绕行方向与电流 成右手螺旋关系时,电流I 为正值;反之I为负值。 B 在磁场中 ,沿任一闭合曲线 矢量的线积 分(也称 矢量的环流),等于真空中的磁导 率 0乘以穿过以这闭合曲线为边界所张任意曲 面的各恒定电流的代数和。 B I为负值 I I为正值 I 绕行方向 上述结论虽是从长直载流导线磁场得来,却具普遍性

fB.dl=∑1 物理意义: B空间所有电流共同产生的磁场 L 在场中任取的一闭合线,任 意规定一个绕行方向 dl L上的任一线元 空间中的电流 ∑I环路所包围的所有电流的代数和 让美下觉返司速此
上页 下页 返回 退出 B 空间所有电流共同产生的磁场 在场中任取的一闭合线,任 意规定一个绕行方向 L l d L上的任一线元 I 空间中的电流 I 环路所包围的所有电流的代数和 物理意义: dl r L I 3 1 I 2 I dl B l = I L d 0

几点注意: ⊙任意形状稳恒电流,安培环路定理都成立。 ⊙环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。 ©安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。 ©静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源
上页 下页 返回 退出 几点注意: 环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。 任意形状稳恒电流,安培环路定理都成立。 安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。 静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源