§7-5电场强度与电势梯度的关系 电势梯度 在电场中任取两相距很近的等势面1和2, 电势分别为V和V+dV,且d>0。 等势面1上P点的单位法向矢量为e。 与等势面2正交于P2点。 在等势面2任取一点P3,设 PP2 dn PP3=dl dr dv 则dn=dl.cosp,d cos o dn V+dV 让意了意适回退块
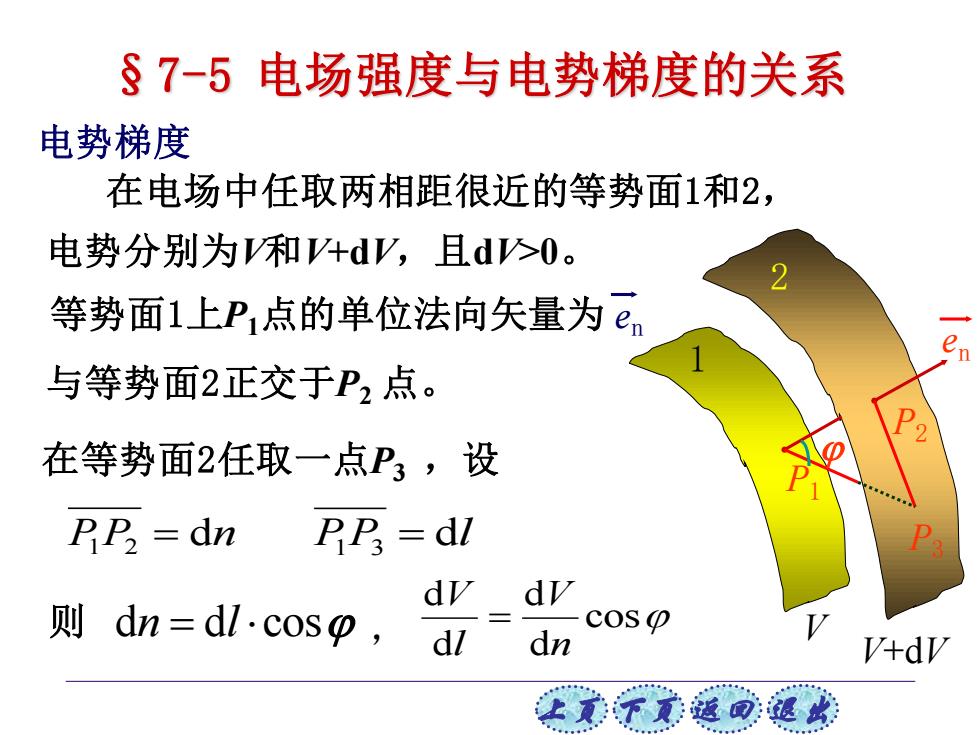
上页 下页 返回 退出 电势梯度 在电场中任取两相距很近的等势面1和2, 1 V V+dV 2 P1 en P2 P3 电势分别为V和V+dV,且dV>0。 等势面1上P1点的单位法向矢量为 en 与等势面2正交于P2 点。 在等势面2任取一点P3 ,设 P1 P2 = dn PP dl 1 3 = 则 dn = dl cos cos d d d d n V l V = §7-5 电场强度与电势梯度的关系
定义电势梯度 gadr=d业。 单位:V/m dn 其量值为该点电势增加率的最大值。 方向与等势面垂直,并指向电势升高的方向。 电势梯度与电场强度的关系 电荷g从等势面1移动到等 势面2,电场力作功 dA=gE.dl =gE·dl.cosp = gE.dn V+dV 让美觉返司退
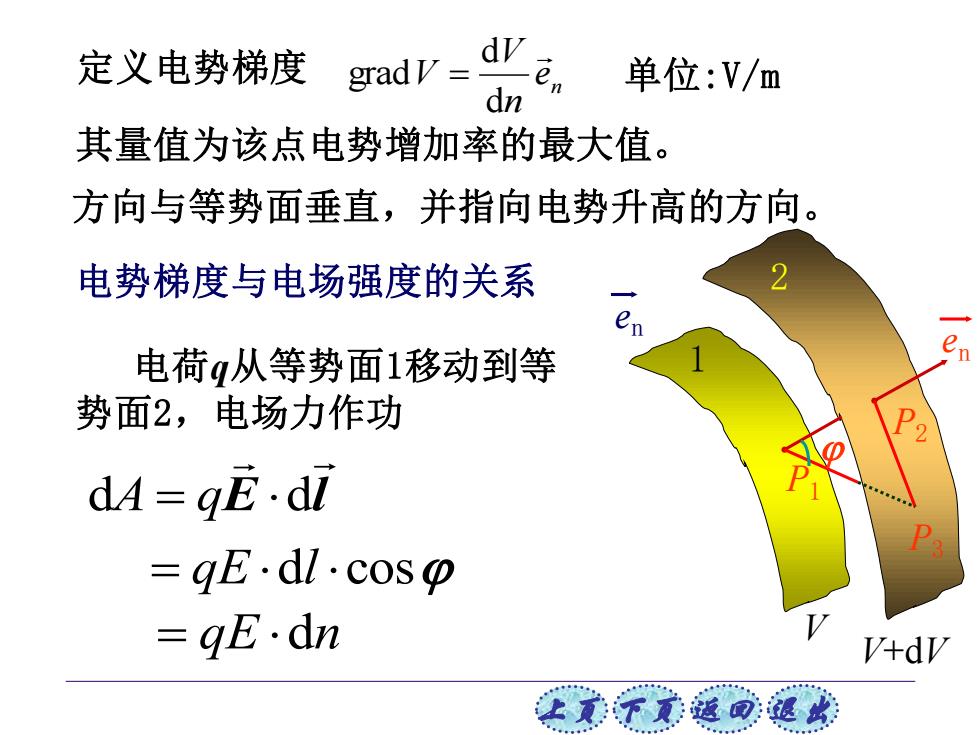
上页 下页 返回 退出 定义电势梯度 n e n V V d d grad = 方向与等势面垂直,并指向电势升高的方向。 其量值为该点电势增加率的最大值。 单位:V/m 1 V V+dV 2 P1 en P2 P3 en 电荷q从等势面1移动到等 势面2,电场力作功 E l dA = q d = qE dl cos = qE dn 电势梯度与电场强度的关系
电场力作功等于电势能的减少量dA=一qd 故 dy E=- dn 场强也与等势面垂直,但指向电势降低的方向。 E- dV dn e =-gradv 写成矢量形式 E=Ee, 在直角坐标系中 E- i+0j+ ay V+dV 让贰子元道觉退此
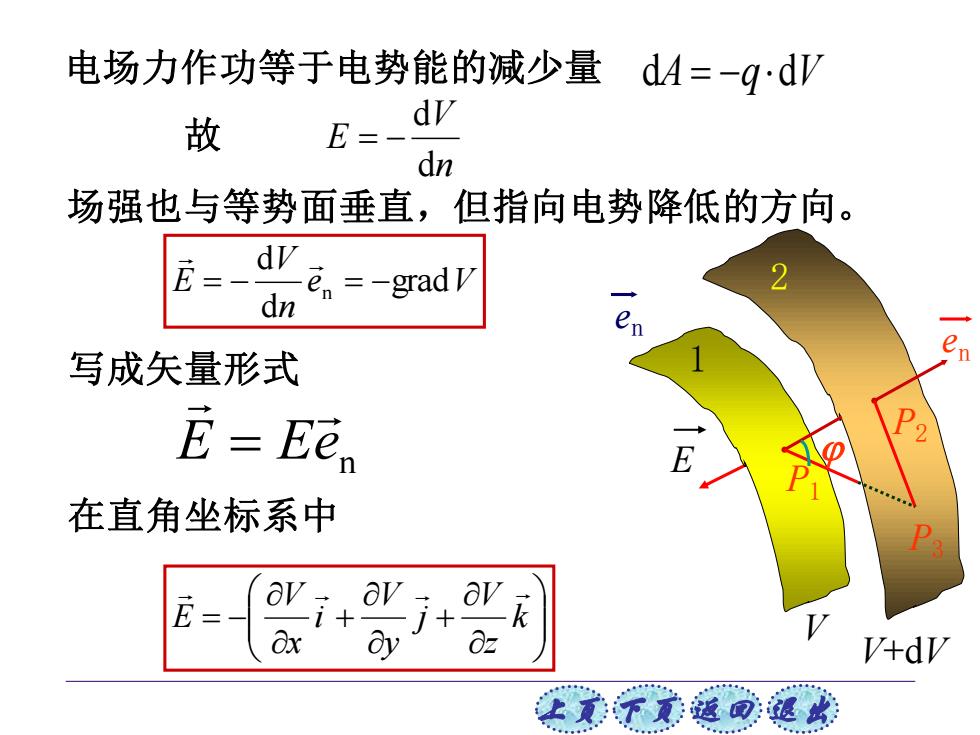
上页 下页 返回 退出 场强也与等势面垂直,但指向电势降低的方向。 电场力作功等于电势能的减少量 dA = −q dV n V E d d = − 写成矢量形式 在直角坐标系中 1 2 E 1 V V+dV 2 P1 en P2 P3 en 故 n E Ee = e V n V E grad d d = − n = − + + = − k z V j y V i x V E
例题7-16 试由电偶极子的电势分布求其的电场强度。 解:在直角坐标系中先写出电势的表达式: V= 19+1二9= g r-r 4πEr+4π60r 4πe0rr+ q Lcose pcosθ P(x,y 4元80 r2 4πE,r2 px 4π6(x2+y2)32 Ex=- ov p(2x2-y) 8 4π(x2+y2)52 ov 3pxy Ey -L/2 4π(x2+y2)52 L 8y 让美觉返司退
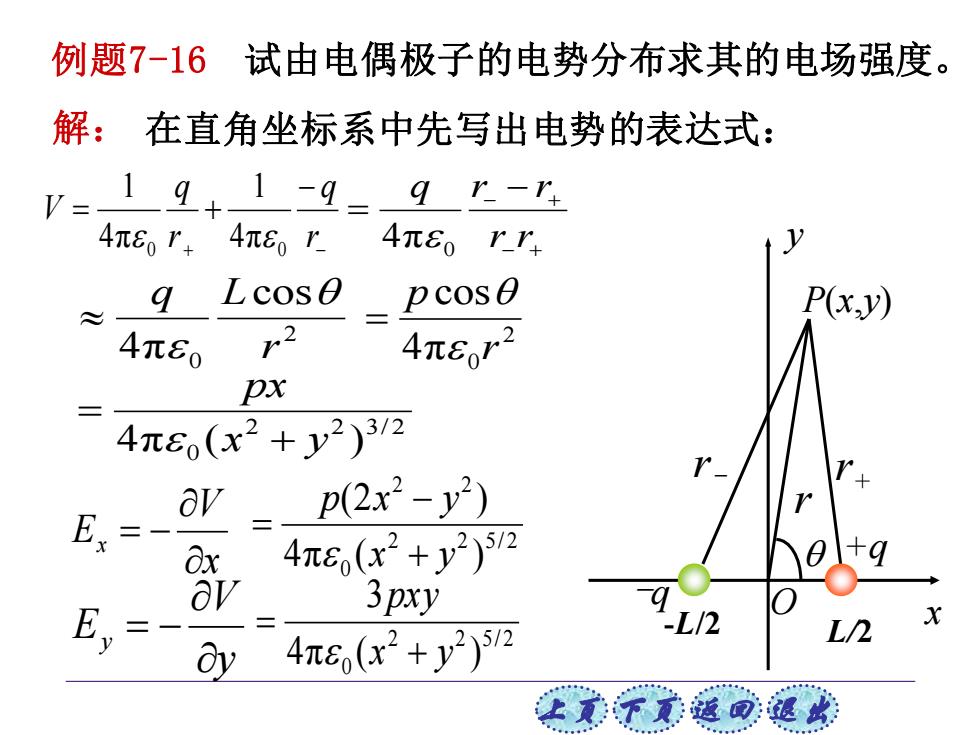
上页 下页 返回 退出 -q 例题7-16 试由电偶极子的电势分布求其的电场强度。 解: 在直角坐标系中先写出电势的表达式: y P(x,y) -L/2 +q L/2 + − − = + r q r q V 0 0 4π 1 4π 1 − + − − + = r r q r r 4π 0 r- r+ r O 2 0 cos 4π r q L 2 4π 0 cos r p = 2 2 3/ 2 0 4π (x y ) px + = x V Ex = − 2 2 5/ 2 0 2 2 4π ( ) (2 ) x y p x y + − = y V Ey = − 2 2 5/ 2 0 4π ( ) 3 x y pxy + = x
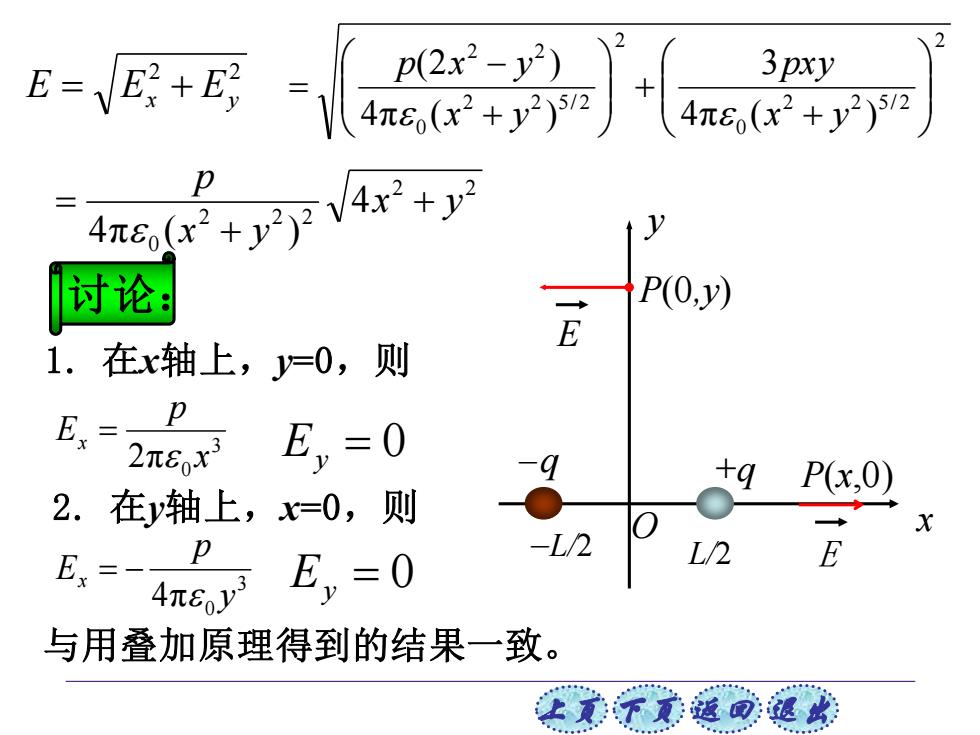
E= -2j p2x2-y2) 3pxy 42+pV4r2+ p 讨论 P(0,y) 1.在x轴上,y=0,则 E= p 2π6x3 E,=0 -q +9P(x,0) 2.在y轴上,x=0,则 -L2 Ex=- ntoy E,=0 E 与用叠加原理得到的结果一致。 上意不意返可:退
上页 下页 返回 退出 1. 在x轴上,y=0,则 3 0 2π x p Ex = Ey = 0 与用叠加原理得到的结果一致。 3 0 4π y p Ex = − Ey = 0 P(x,0) -L/2 L/2 x y O E - +q q P(0,y) E 2. 在y轴上,x=0,则 2 2 E = Ex + Ey 2 2 2 5/ 2 0 2 2 2 5/ 2 0 2 2 4π ( ) 3 4π ( ) (2 ) + + + − = x y pxy x y p x y 2 2 2 2 2 0 4 4π ( ) x y x y p + + = 讨论:
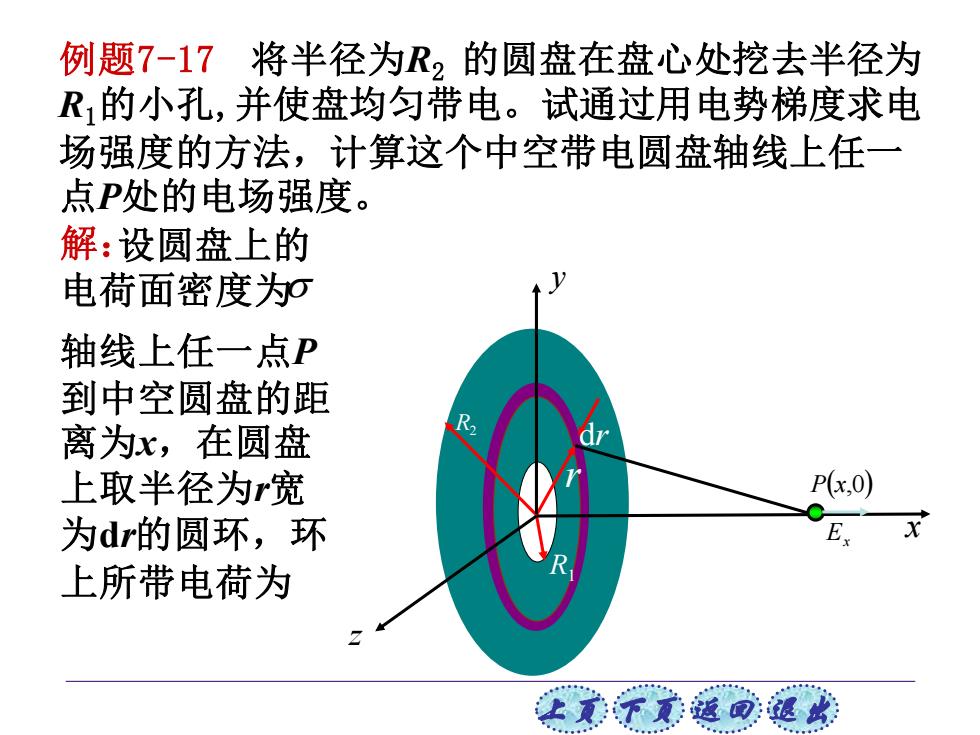
例题7-17将半径为R2的圆盘在盘心处挖去半径为 R的小孔,并使盘均匀带电。试通过用电势梯度求电 场强度的方法,计算这个中空带电圆盘轴线上任一 点P处的电场强度。 解:设圆盘上的 电荷面密度为∞ 轴线上任一点P 到中空圆盘的距 离为x,在圆盘 上取半径为r宽 P(x,0) 为dr的圆环,环 E. 上所带电荷为 让美觉返司退
上页 下页 返回 退出 例题7-17 将半径为R2 的圆盘在盘心处挖去半径为 R1的小孔,并使盘均匀带电。试通过用电势梯度求电 场强度的方法,计算这个中空带电圆盘轴线上任一 点P处的电场强度。 R2 R1 r dr x y z P(x,0) Ex 解:设圆盘上的 电荷面密度为 轴线上任一点P 到中空圆盘的距 离为x,在圆盘 上取半径为r宽 为dr的圆环,环 上所带电荷为

dg =2nrodr 该圆环在P点的电势为 dq ordr dV 4,(2+x2,(2+r 整个中空圆盘在该点的电势为 r-ar-a品k+-风) ordr 由于电荷的轴对称分布,E,=E。=0 av E=E=- 让贰不贰适可退晚
上页 下页 返回 退出 该圆环在P点的电势为 整个中空圆盘在该点的电势为 ( ) 2 2 1 2 2 2 2 0 = R + x − R + x x V E Ex = = − + − + = 2 2 2 2 2 1 2 0 R x x R x x 由于电荷的轴对称分布, Ey = Ez = 0 dq = 2πrdr ( ) ( ) 1 2 1 2 2 2 2 2 0 0 d d d 4π 2 q r r V r x r x = = + + ( ) + = = 2 1 2 1 1 2 2 2 2 0 d d R R R R r x r r V V

选择进入下一节 §7-0教学基本要求 §7-1物质的电结构 库仑定律 §7-2静电场电场强度 §7-3 静电场的高斯定律 §7-4静电场的环路定律电势 §7-5电场强度与电势梯度的关系 §7-6静电场中的导体 §7-7电容器的电容 §78静电场中的电介质 §79有电介质时的高斯定律 电位移 §7-10静电场的能量 让美下觉返同速
上页 下页 返回 退出 选择进入下一节 §7-0 教学基本要求 §7-1 物质的电结构 库仑定律 §7-2 静电场 电场强度 §7-3 静电场的高斯定律 §7-4 静电场的环路定律 电势 §7-5 电场强度与电势梯度的关系 §7-6 静电场中的导体 §7-7 电容器的电容 §7-8 静电场中的电介质 §7-9 有电介质时的高斯定律 电位移 §7-10 静电场的能量