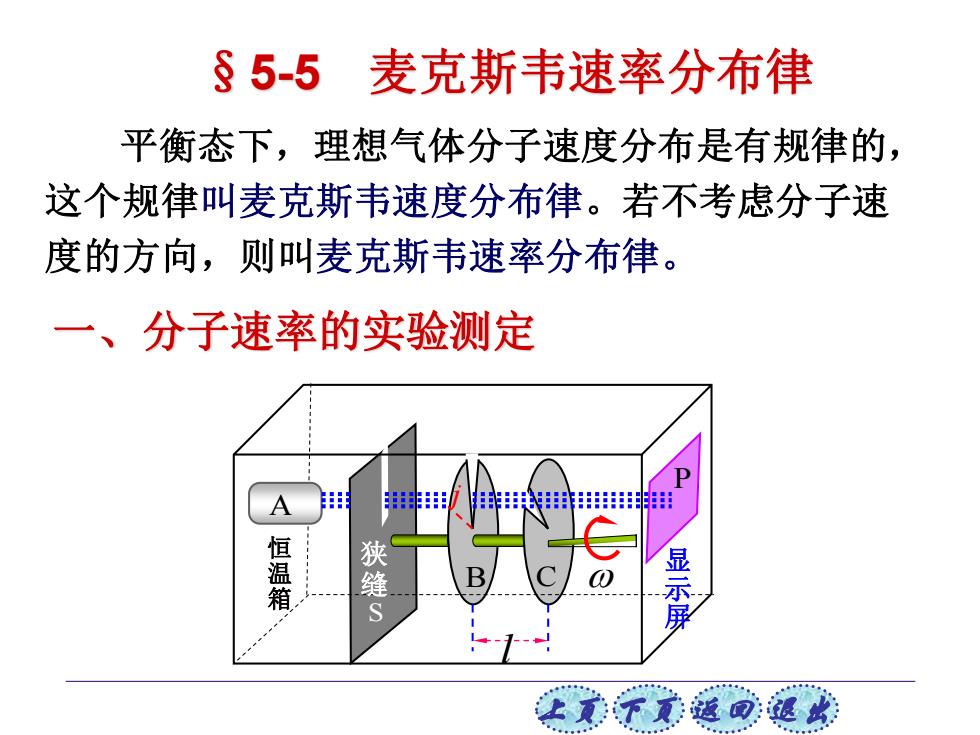
§5-5 麦克斯韦速率分布律 平衡态下,理想气体分子速度分布是有规律的, 这个规律叫麦克斯韦速度分布律。若不考虑分子速 度的方向,则叫麦克斯韦速率分布律。 一、分子速率的实验测定 A 球田 田非出 恒温箱 狭 显示 S
上页 下页 返回 退出 平衡态下,理想气体分子速度分布是有规律的, 这个规律叫麦克斯韦速度分布律。若不考虑分子速 度的方向,则叫麦克斯韦速率分布律。 一、分子速率的实验测定 §5-5 麦克斯韦速率分布律 l A 显 示 屏 狭 缝 j S B C P 恒 温 箱

当圆盘以角速度ω转动时,只有满足下列关系 式的分子才能通过C的狭缝射到屏P上。 V= 而其他速率的分子则将沉积在槽壁上,小孔充 分小,改变角速度0,用光度学方法测量各次在胶 片上所沉积的金属层厚度,可得气体速率分布。 让美下觉返司速此
上页 下页 返回 退出 = = v l t v l = 当圆盘以角速度 转动时,只有满足下列关系 式的分子才能通过C的狭缝射到屏P上。 而其他速率的分子则将沉积在槽壁上,小孔充 分小,改变角速度,用光度学方法测量各次在胶 片上所沉积的金属层厚度,可得气体速率分布
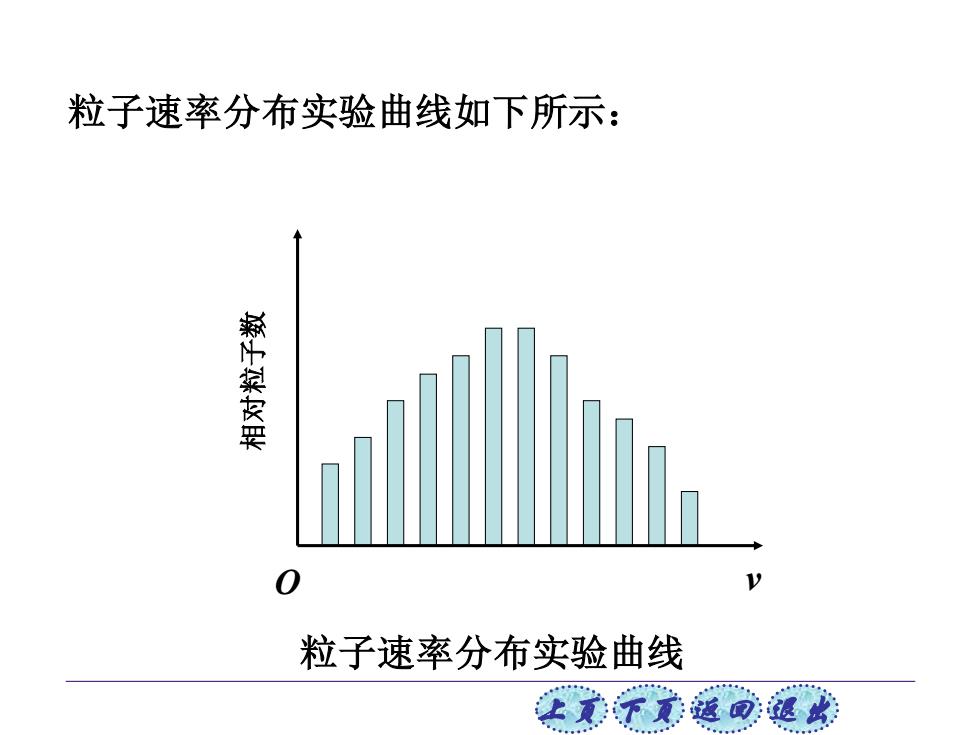
粒子速率分布实验曲线如下所示: 粒子速率分布实验曲线 E意子素道回退
上页 下页 返回 退出 O v 粒子速率分布实验曲线 粒子速率分布实验曲线如下所示: 相对粒子数

二、速率分布函数 1.研究气体分子的速率分布 ·把速率分成若干相等区间 ·求气体在平衡态下分布在各区间内的分子数 ·各区间的分子数占气体分子总数的百分比 速率分布:把速率可能出现的值分成若干相等区间, 全部分子如何分配到这些区间中去的问题。 分布表 分布曲线 分布函数 将速率分成若干相等的区间,如 0~0+10m/s:10m/s~10m/s+10m/s; 20m/s~20m/s+10m/s,30m/s~30m/s+10m/s,. 王文不美菠面:退收
上页 下页 返回 退出 二、 速率分布函数 将速率分成若干相等的区间,如 0 ~ 0 10m/s;10m / s ~ 10m / s 10m / s; + + 20m / s ~ 20m / s 10m / s;30m / s ~ 30m / s 10m / s; + + 1.研究气体分子的速率分布 • 把速率分成若干相等区间 • 求气体在平衡态下分布在各区间内的分子数 • 各区间的分子数占气体分子总数的百分比 速率分布:把速率可能出现的值分成若干相等区间, 全部分子如何分配到这些区间中去的问题。 分布表 分布曲线 分布函数
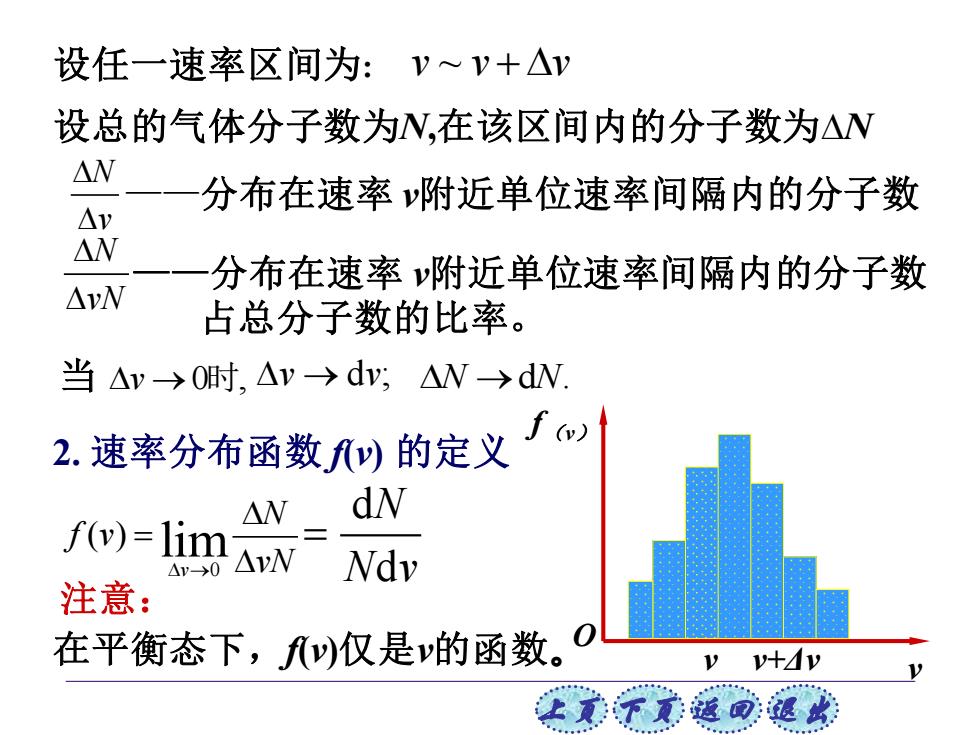
设任一速率区间为:v~v+△v 设总的气体分子数为N,在该区间内的分子数为△N △N 分布在速率附近单位速率间隔内的分子数 △y △W 分布在速率v附近单位速率间隔内的分子数 △W 占总分子数的比率。 当△v→0时,△v→dv;△N→dN. 2.速率分布函数fy)的定义 △W dN )lin Aw Ndv 注意: 在平衡态下,)仅是的函数。0 让贰不觉返回退
上页 下页 返回 退出 设任一速率区间为: 设总的气体分子数为N,在该区间内的分子数为N ——分布在速率 v附近单位速率间隔内的分子数 ——分布在速率 v附近单位速率间隔内的分子数 占总分子数的比率。 当 2. 速率分布函数 f(v) 的定义 在平衡态下,f(v)仅是v的函数。 注意: v f(v) O v v+Δv N v N vN →v 0 , 时 →v vd ; →N Nd . 0 ( ) lim v N f v → vN = d d N N v = v v v ~ +
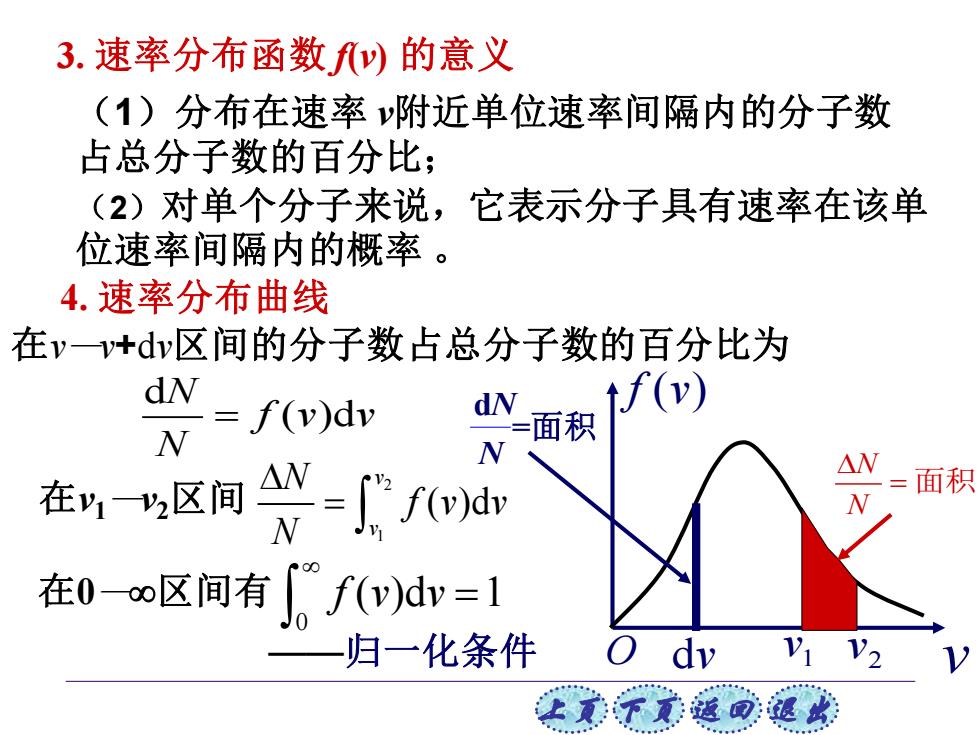
3.速率分布函数fv的意义 (1)分布在速率附近单位速率间隔内的分子数 占总分子数的百分比; (2)对单个分子来说,它表示分子具有速率在该单 位速率间隔内的概率。 4.速率分布曲线 在vv+dv区间的分子数占总分子数的百分比为 dN .f(v) _=f(v)dv 面积 N 在区间广 面积 在0o∞区间有。f(v)dw=1 归一化条件 VI V2 让美觉返司退此
上页 下页 返回 退出 3. 速率分布函数 f(v) 的意义 (1)分布在速率 v附近单位速率间隔内的分子数 占总分子数的百分比; (2)对单个分子来说,它表示分子具有速率在该单 位速率间隔内的概率 。 4. 速率分布曲线 在v—v+dv区间的分子数占总分子数的百分比为 在0—区间有 0 f v v ( )d 1 = ——归一化条件 在v1—v2区间 2 1 ( )d v v N f v v N = f v( ) O dv 1 v v 2 v d ( )d N f v v N = dN N =面积 N N = 面积
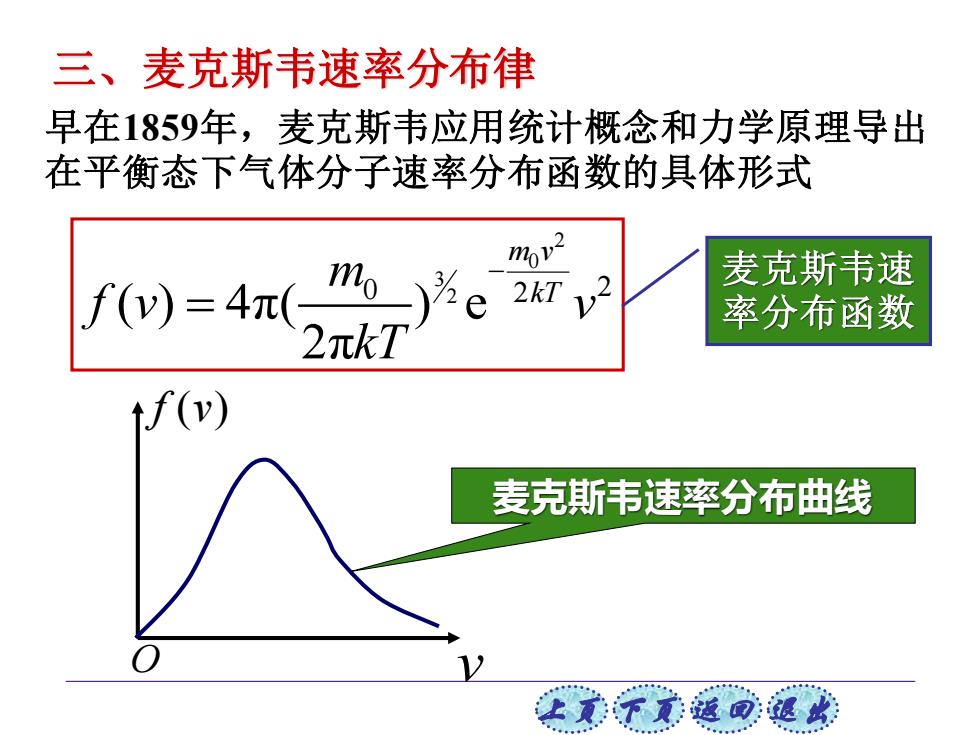
三、麦克斯韦速率分布律 早在1859年,麦克斯韦应用统计概念和力学原理导出 在平衡态下气体分子速率分布函数的具体形式 mov 麦克斯韦速 f()=4π( e 2kT 元kT 率分布函数 1f(v) 麦克斯韦速率分布曲线 让无子文返回退此
上页 下页 返回 退出 三、麦克斯韦速率分布律 早在1859年,麦克斯韦应用统计概念和力学原理导出 在平衡态下气体分子速率分布函数的具体形式 2 0 3 0 2 2 2 ( ) 4π( ) e 2π m v m kT f v v kT − = 麦克斯韦速 率分布函数 f (v) O v 麦克斯韦速率分布曲线

例题5-5从速率分布函数推算分子速率的三个统计平均值 (1)算术平均速率 2 =Df()v=04π( mo e y'dv 2πkT 8kT RT ≈1.6 m, (2)方均根速率 %2 -F咖w=427。 3kT 3RT RT ≈1.73 mo M ol 让美下元返回:退欢
上页 下页 返回 退出 例题5-5 从速率分布函数推算分子速率的三个统计平均值 (1)算术平均速率 (2)方均根速率 0 v vf v v ( )d = 2 0 3 0 2 2 2 0 4π( ) e d 2π m v m kT v v v kT − = 0 8 π kT m = mol 8 π RT M = mol 1.6 RT M 2 2 0 v v f v v ( )d = 2 0 3 2 2 0 2 2 0 4π( ) e d 2π m v m kT v v v kT − = 2 0 3kT v m = mol 3RT M = mol 1.73 RT M
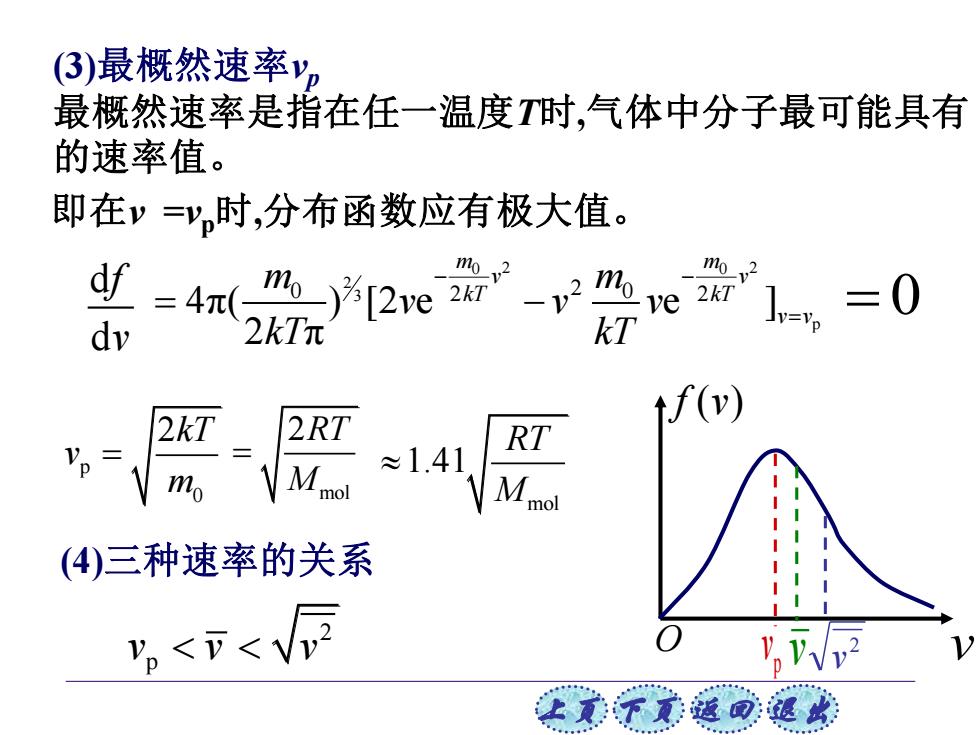
(3)最概然速率y, 最概然速率是指在任一温度T时,气体中分子最可能具有 的速率值。 即在y=,时,分布函数应有极大值。 =4n(m)2vemve mo v2 =0 dy 2kT元 kT f(v) 2kT 2RT RT Vp= ≈1.41 mo M mol Mmol (4)三种速率的关系 VVVv2 让美下意通回退此
上页 下页 返回 退出 (3)最概然速率vp 最概然速率是指在任一温度T时,气体中分子最可能具有 的速率值。 (4)三种速率的关系 即在v =vp时,分布函数应有极大值。 d d f v 0 0 2 2 2 3 p 0 0 2 2 2 4π( ) [2 e e ] 2 π m m v v kT kT v v m m v v v kT kT − − = − = p 0 2kT v m = mol 2RT M = mol 1.41 RT M 2 p v v v = 0 f (v) O vp v v 2 v
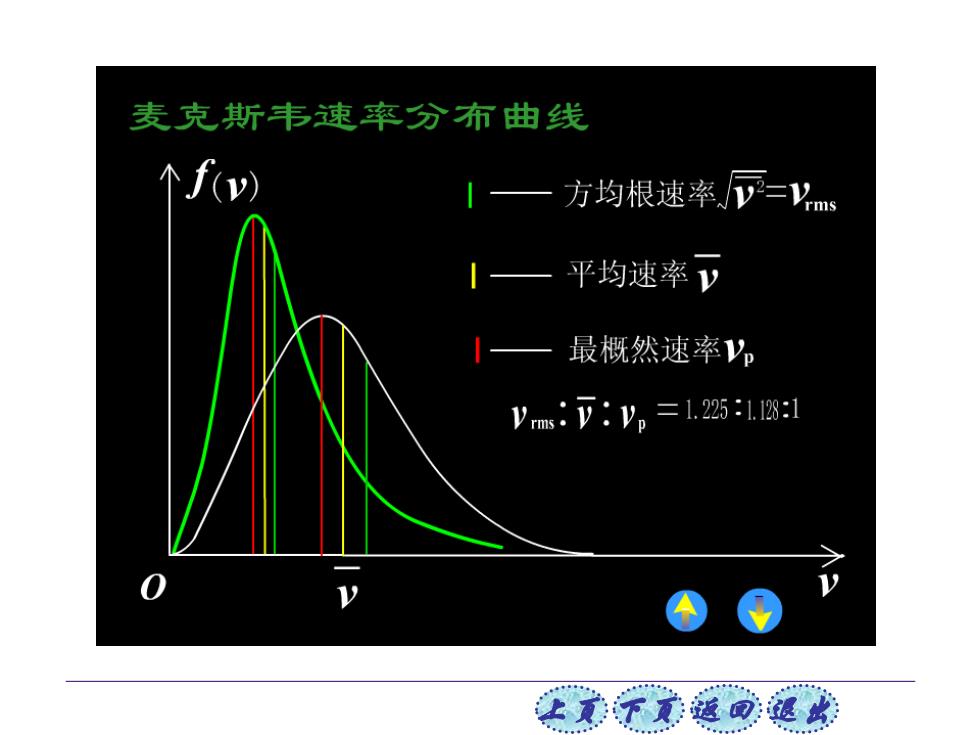
麦克斯韦速率分布曲线 个f(v) 方均根速率=ms 平均速率y 最概然速率。 VmsV:y。=1.251181 让美觉返司退
上页 下页 返回 退出