
§3-1刚体模型及其运动 一 般的力学分析方法可归纳为: (1)突出主要矛盾,撇开次要因素,建立理想模型; (2)将质点系化整为零,以质点或质元为研究对象, 作为突破口; (3)根据受力情况,正确画出受力图; (4)根据已知条件或初始条件,选用所需的基本原 理、定律,列出方程式: (5)根据要求,求解方程,统一变量,积零为整,用 积分法求出结果。积分上下限的选取要特别注意; (6)讨论分析所得结果,检验是否正确。 现在将这些方法用于刚体和流体的研究。 让无子文道回退此
上页 下页 返回 退出 一般的力学分析方法可归纳为: (1)突出主要矛盾,撇开次要因素,建立理想模型; (2)将质点系化整为零,以质点或质元为研究对象, (3)根据受力情况,正确画出受力图; (4)根据已知条件或初始条件,选用所需的基本原 (5)根据要求,求解方程,统一变量,积零为整,用 (6)讨论分析所得结果,检验是否正确。 现在将这些方法用于刚体和流体的研究。 §3- 1刚体模型及其运动 作为突破口; 理、定律,列出方程式; 积分法求出结果。 积分上下限的选取要特别注意;

一、刚体 刚体:在外力的作用下,大小和形状都不变的物体 - 物体内任意两点的距离不变。 刚体运动研究的基础:刚体是由无数个连续分布的 质点组成的质点系,每个质点称为刚体的一个质量 元dm。每个质点运动都服从质点力学规律。刚体的 运动是这些质量元运动的总和。 二、平动和转动 1.平动 当刚体运动时,如果刚体内任何一条给定的直线,在 运动中始终保持它的方向不变,这种运动叫平动。 让美觉返司退
上页 下页 返回 退出 刚体运动研究的基础:刚体是由无数个连续分布的 质点组成的质点系,每个质点称为刚体的一个质量 元dm。每个质点运动都服从质点力学规律。刚体的 运动是这些质量元运动的总和。 二、平动和转动 刚体:在外力的作用下,大小和形状都不变的物体 -物体内任意两点的距离不变。 当刚体运动时,如果刚体内任何一条给定的直线,在 运动中始终保持它的方向不变,这种运动叫平动。 一、刚体 1.平动
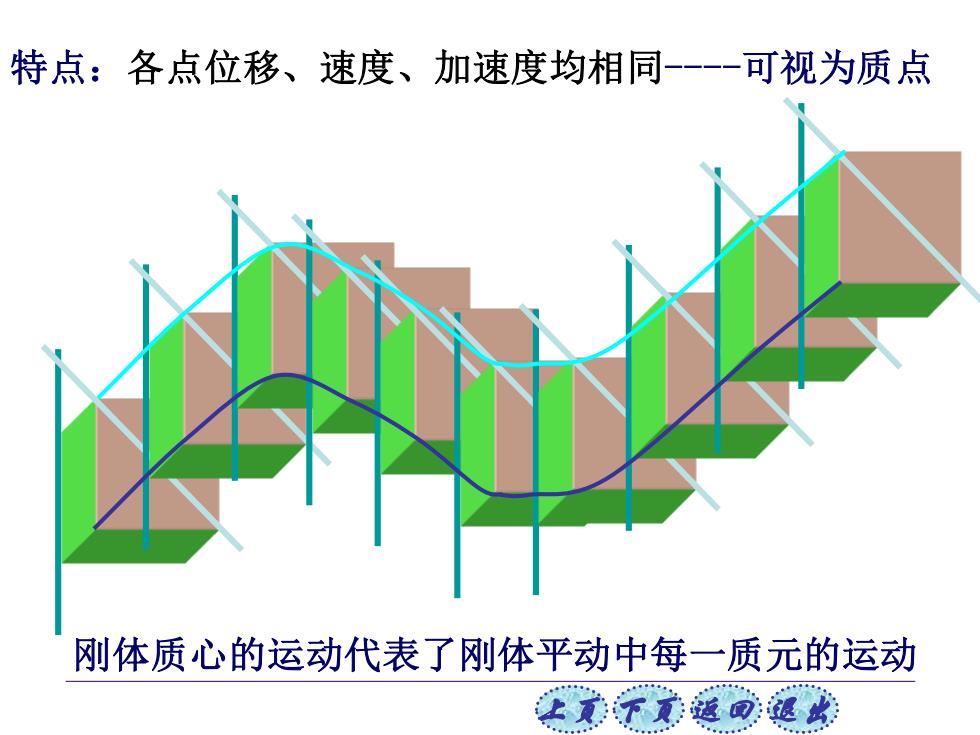
特点:各点位移、速度、加速度均相同-可视为质点 刚体质心的运动代表了刚体平动中每一质元的运动 让无子文道回退此
上页 下页 返回 退出 刚体质心的运动代表了刚体平动中每一质元的运动 特点:各点位移、速度、加速度均相同-可视为质点

2.转动 刚体运动时,如果刚体的各个质点在运动中都绕 同一直线作圆周运动,这种运动就叫做转动,这一直 线就叫做转轴。 (1)定轴转动:转轴相对参考系静止。 (2)定点转动:转轴上只有一点相对参考系静止, 转轴方向不断变化。 让美下觉返同速
上页 下页 返回 退出 刚体运动时,如果刚体的各个质点在运动中都绕 同一直线作圆周运动,这种运动就叫做转动,这一直 线就叫做转轴。 2.转动 (1)定轴转动:转轴相对参考系静止。 (2)定点转动:转轴上只有一点相对参考系静止, 转轴方向不断变化
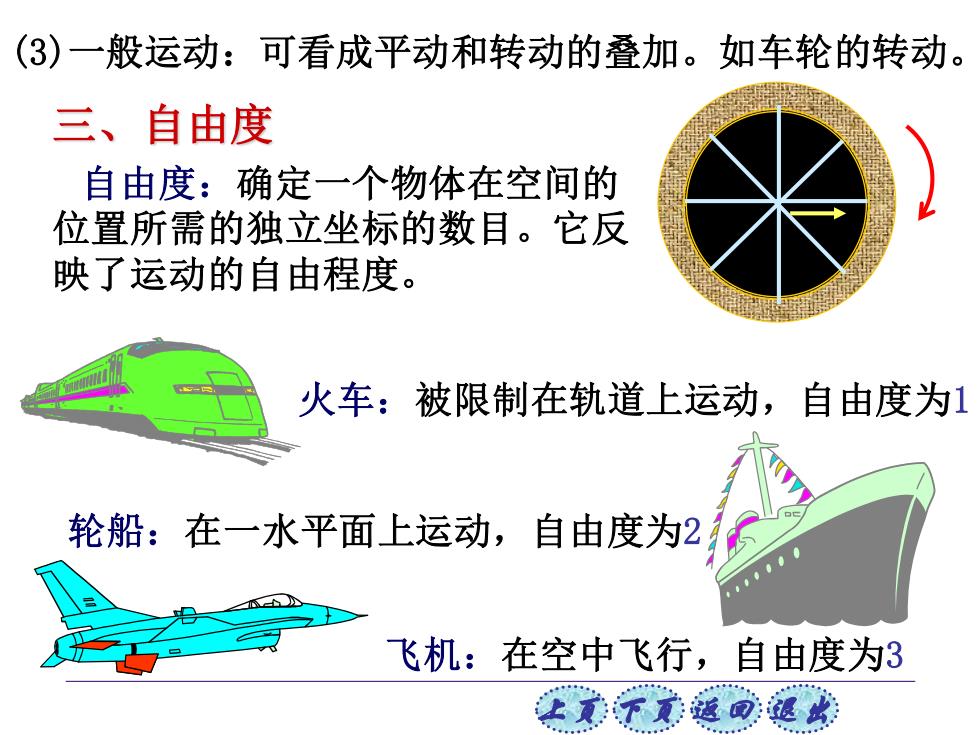
(3)一般运动:可看成平动和转动的叠加。如车轮的转动。 三、自由度 自由度:确定一个物体在空间的 位置所需的独立坐标的数目。它反 映了运动的自由程度。 火车:被限制在轨道上运动,自由度为1 轮船:在一水平面上运动,自由度为2 飞机:在空中飞行,自由度为3 子元道回退瑞
上页 下页 返回 退出 三、自由度 自由度:确定一个物体在空间的 位置所需的独立坐标的数目。它反 映了运动的自由程度。 火车:被限制在轨道上运动,自由度为1 飞机:在空中飞行,自由度为3 轮船:在一水平面上运动,自由度为2 (3)一般运动:可看成平动和转动的叠加。如车轮的转动
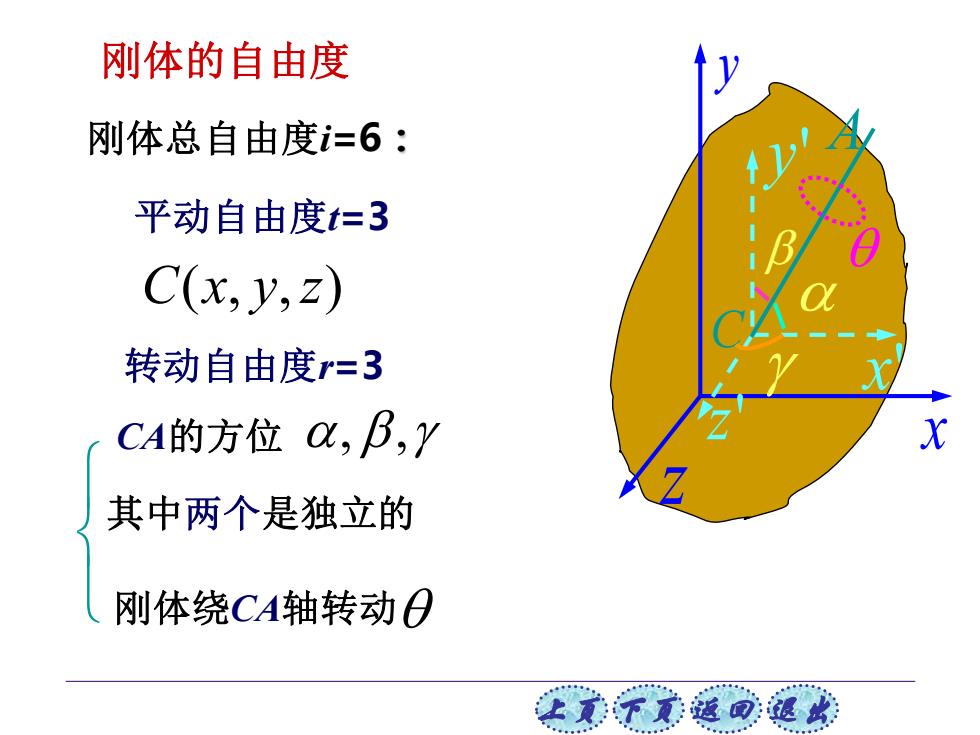
刚体的自由度 刚体总自由度i=6: 平动自由度t=3 C(x,y,2) 转动自由度r=3 CA的方位C,B,Y X 其中两个是独立的 刚体绕CA轴转动O 上文不美返回退球
上页 下页 返回 退出 刚体的自由度 x y z C x' y' z' A 刚体总自由度i=6: 平动自由度t=3 转动自由度r=3 C x y z ( , , ) 刚体绕CA轴转动 CA的方位 , , 其中两个是独立的

选择进入下一节 §3-0教学基本要求 §3-1刚体模型及其运动 §3-2力矩转动惯量定轴转动定律 §33定轴转动中的功能关系 §3-4定轴转动刚体的角动量定律和角动量守恒定律 *§3-5进动 *§3-6理想流体模型 定常流动伯努利方程 *§3-7牛顿力学的内在随机性混沌 上美不京返可退此
上页 下页 返回 退出 选择进入下一节 §3-0 教学基本要求 §3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系 §3-4 定轴转动刚体的角动量定律和角动量守恒定律 *§3-5 进动 *§3-6 理想流体模型 定常流动 伯努利方程 *§3-7 牛顿力学的内在随机性 混沌