
§1-1质点运动的描述 一、质点 物体:具有大小、形状、质量和内部结构的物质形态。 一般情况下,物体各部分的运动不相同,在运动 的过程中大小、形状可能改变,这使得运动问题变得 复杂。 某些情况下,物体的大小、形状不起作用,或者 起次要作用而可以忽略其影响一一简化为质点模型。 质点:具有一定质量而大小或形状可以忽略的理想物体 上元子京返或退此
上页 下页 返回 退出 一、质点 物体:具有大小、形状、质量和内部结构的物质形态。 质点:具有一定质量而大小或形状可以忽略的理想物体。 一般情况下,物体各部分的运动不相同,在运动 的过程中大小、形状可能改变,这使得运动问题变得 复杂。 某些情况下,物体的大小、形状不起作用,或者 起次要作用而可以忽略其影响——简化为质点模型。 §1-1 质点运动的描述
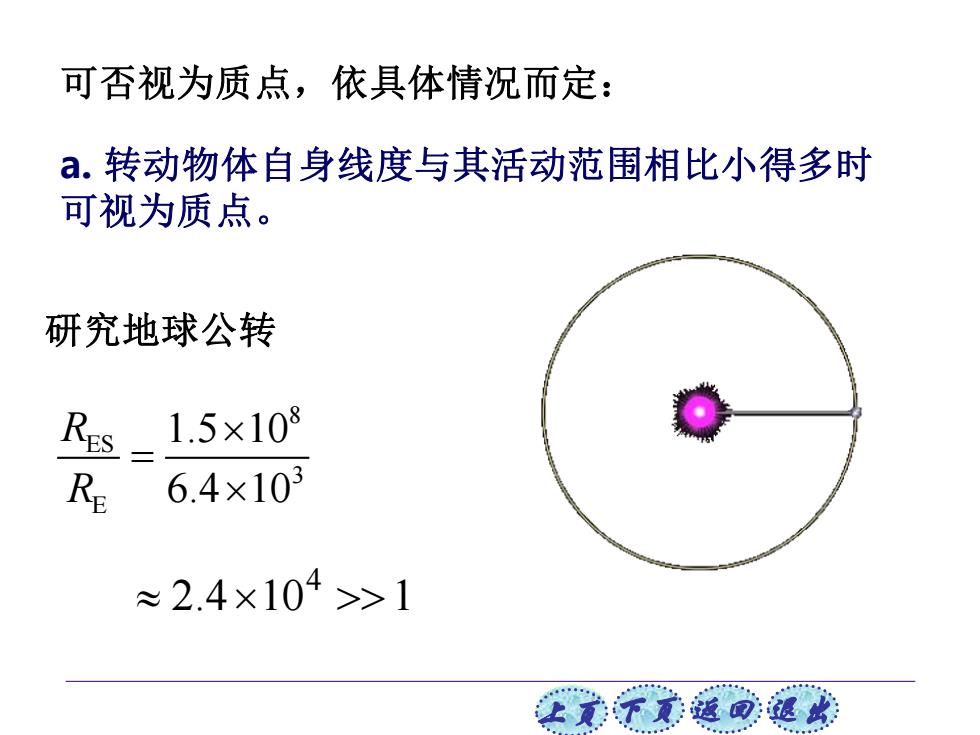
可否视为质点,依具体情况而定: a.转动物体自身线度与其活动范围相比小得多时 可视为质点。 研究地球公转 Res 1.5×108 RE 6.4×103 ≈2.4×104>1 正觉不美返回退
上页 下页 返回 退出 研究地球公转 8 ES 3 E 1.5 10 6.4 10 R R = 2.4 10 1 4 a. 转动物体自身线度与其活动范围相比小得多时 可视为质点。 可否视为质点,依具体情况而定:

研究地球自转 y=@R 地 地球上各点的 速度相差很大, 因此,地球自 身的大小和形 状不能忽略, 这时不能作质 点处理。 让意订套返可退斯
上页 下页 返回 退出 研究地球自转 v =R 地球上各点的 速度相差很大, 因此,地球自 身的大小和形 状不能忽略, 这时不能作质 点处理

b.物体平动时可视为质点。 物体上任一点的运动都可以代表物体的运动。 正流下意返司退
上页 下页 返回 退出 b. 物体平动时可视为质点。 物体上任一点的运动都可以代表物体的运动

二、参考系和坐标系 1.为什么要选用参考系 例如:匀速运动车厢内某人竖直下抛一小球,观 察小球的运动状态。 车厢内的人:竖直下落 地面上的人:抛物运动 孰是孰非? 运动的描述是相对的 士元子意返可退
上页 下页 返回 退出 二、参考系和坐标系 1.为什么要选用参考系 车厢内的人: 竖直下落 地面上的人: 抛物运动 ——运动的描述是相对的 例如:匀速运动车厢内某人竖直下抛一小球,观 察小球的运动状态。 孰是孰非?

2.什么是参考系 参考系:为描述物体运动而选用的标准物体或物体系。 坐标系:为了定量描述物体的位置与运动情况,在定 的参考系上建立的带有标尺的数学坐标,称 坐标系。 常用的坐标系有直角坐标系(c,y,z),极坐标 系(p,O),球坐标系(R,O,p),柱坐标系(R,p,z)。 参考方向 江子元道回退此
上页 下页 返回 退出 参考系:为描述物体运动而选用的标准物体或物体系。 2.什么是参考系 坐标系:为了定量描述物体的位置与运动情况,在定 的参考系上建立的带有标尺的数学坐标,称 坐标系。 常用的坐标系有直角坐标系(x , y , z),极坐标 系( , ),球坐标系(R , , ),柱坐标系(R , , z)。 x y z O z R 参考方向 z O、 R x y

三、空间和时间 空间反映了物质的广延性,与物体的体积和位 置的变化联系在一起。 时间反映物理事件的顺序性和持续性,与物理 事件的变化发展过程联系在一起。 各个时代有代表性的时空观: 墨子:空间是一切不同位置的概括和抽象;时 间是一切不同时刻的概括和抽象。 莱布尼兹:空间和时间是物质上下左右的排列 形式和先后久暂的持续形式,没有具体的物质和物 质的运动就没有空间和时间,强调时间和空间的客 观性而忽略与运动的联系
上页 下页 返回 退出 空间反映了物质的广延性,与物体的体积和位 置的变化联系在一起。 时间反映物理事件的顺序性和持续性,与物理 事件的变化发展过程联系在一起。 各个时代有代表性的时空观: 墨子:空间是一切不同位置的概括和抽象;时 间是一切不同时刻的概括和抽象。 三、空间和时间 莱布尼兹:空间和时间是物质上下左右的排列 形式和先后久暂的持续形式,没有具体的物质和物 质的运动就没有空间和时间,强调时间和空间的客 观性而忽略与运动的联系

牛顿:空间和时间是不依赖于物质的独立的客 观存在,强调与运动的联系忽略客观性。 爱因斯坦:相对论时空观,时间与空间客观 存在,与运动密不可分。 目前的时空观范围:宇宙的尺度1026m(20亿光 年)到微观粒子尺度1015m,从宇宙的年龄1018s(20 亿年,宇宙年龄)到微观粒子的最短寿命1024s。 物理理论指出,空间和时间都有下限:分别为 普朗克长度1035m和普朗克时间1043s。 士元子元道回退收
上页 下页 返回 退出 牛顿:空间和时间是不依赖于物质的独立的客 观存在,强调与运动的联系忽略客观性。 爱因斯坦:相对论时空观,时间与空间客观 存在,与运动密不可分。 目前的时空观范围:宇宙的尺度1026m(20亿光 年)到微观粒子尺度10_ 15m,从宇宙的年龄1018s(20 亿年,宇宙年龄)到微观粒子的最短寿命10_ 24s。 物理理论指出,空间和时间都有下限:分别为 普朗克长度10_ 35m和普朗克时间10_ 43s

四、运动学方程 在一定的坐标系中,质点的位置随时间按一 定规律变化,位置用坐标表示为时间的函数,叫 做运动方程。 x=x(t) 运动方程:下=(t)一y=(t) f(x,y,z)=0 Z=z(t) 轨道方程:f(xy,2)=0 运动方程与轨道方程的关系: 将运动方程中的时间消去, 得到质点运动的轨道方程
上页 下页 返回 退出 ( ) ( ) ( ) ( ) x x t r r t y y t z z t = = = = f (x, y,z) = 0 将运动方程中的时间消去, 得到质点运动的轨道方程。 f (x, y,z) = 0 z o x y P(x,y,z) i k j 运动方程: 轨道方程: 运动方程与轨道方程的关系: 在一定的坐标系中,质点的位置随时间按一 定规律变化,位置用坐标表示为时间的函数,叫 做运动方程。 四、运动学方程
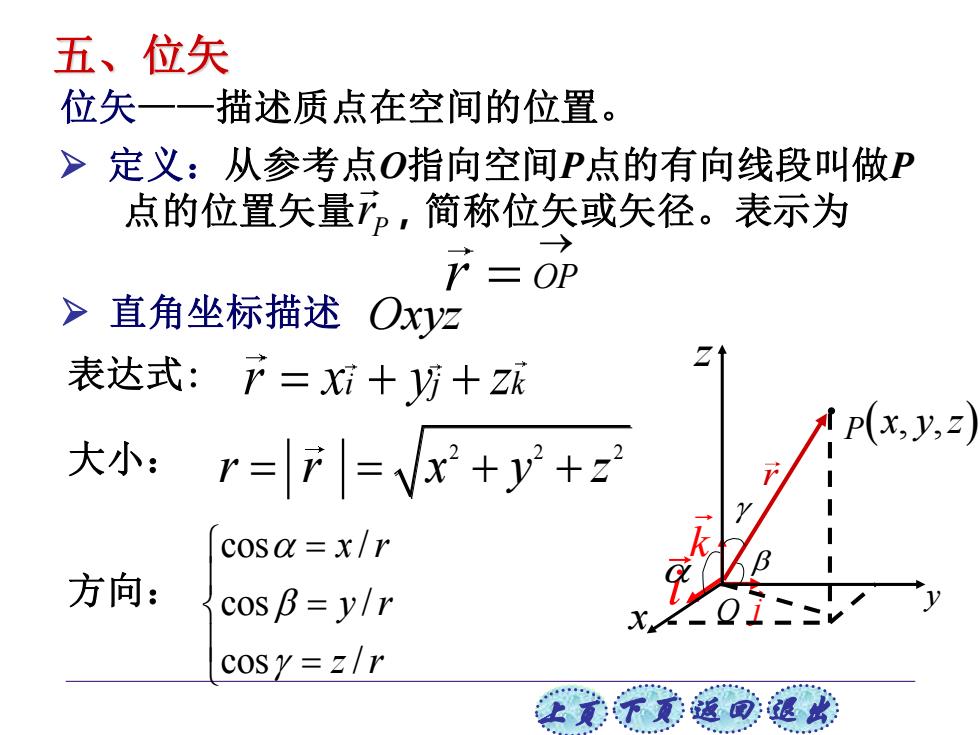
五、位矢 位矢一一描述质点在空间的位置。 >定义:从参考点O指向空间P点的有向线段叫做P 点的位置矢量Tp,简称位矢或矢径。表示为 r=OP >直角坐标描述Oxyz 表达式:下=+听+Z弧 p(x,y,Z 大小:r=F=Vx2+y+z cosa=x/r 方向: cosB=y/r cosy=z/r 正美下意返同退
上页 下页 返回 退出 O P r j k i x y z ➢ 直角坐标描述 Oxyzr OP → = ➢ 定义:从参考点O指向空间P点的有向线段叫做P 点的位置矢量 rP ,简称位矢或矢径。表示为 位矢——描述质点在空间的位置。 ( x y z , , ) 表达式: r x y z = + + i j k 2 2 2 大小: r r x y z = = + + 方向: cos / cos / cos / x r y r z r = = = 五、位矢