§25质点系的功能原理机械能守恒定律 一、质点系的动能定理 多个质点组成的质点系,既要考虑外力,又要 考虑质点间的相互作用力(内力)。 两个质点组成 两个质点在外力及内 的系统 力作用下如图所示: F 推 my F m2 多个质点组成 的系统 让意不觉返可退此
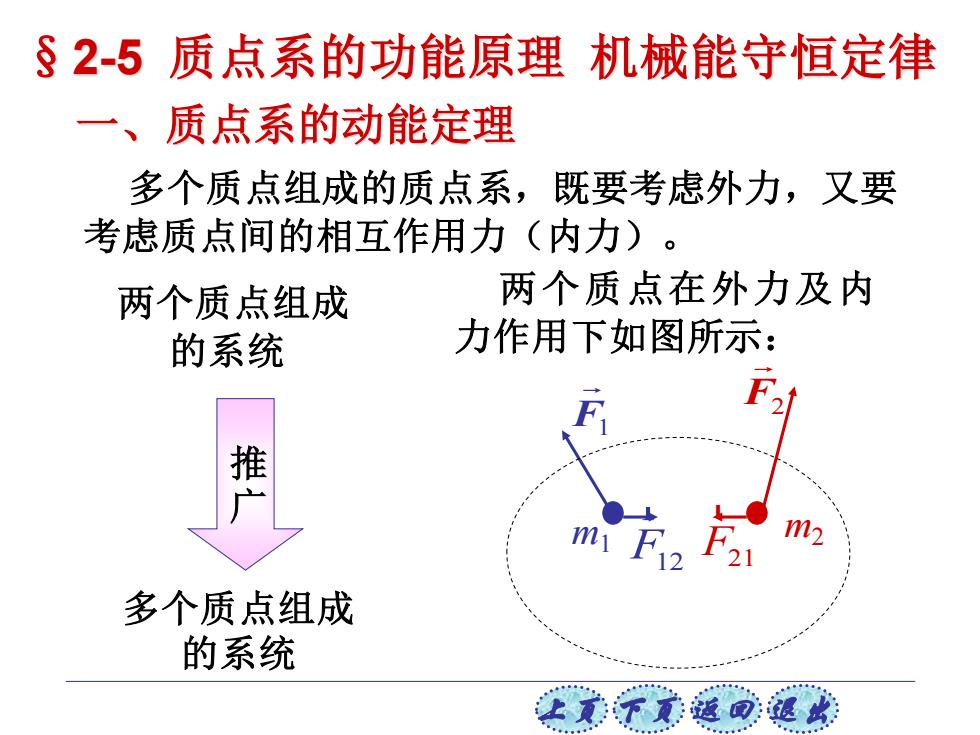
上页 下页 返回 退出 多个质点组成的质点系,既要考虑外力,又要 考虑质点间的相互作用力(内力)。 F1 F2 F12 r F21 r m1 m2 两个质点组成 的系统 多个质点组成 的系统 两个质点在外力及内 力作用下如图所示: 推 广 一、质点系的动能定理 §2-5 质点系的功能原理 机械能守恒定律
对m1运用质点动能定理: 心斤-d听+小ad听=叫层-网呢 对m2运用质点动能定理: F 心序d店+d店 ,21 m方2 m2 王美不美菠回:退收
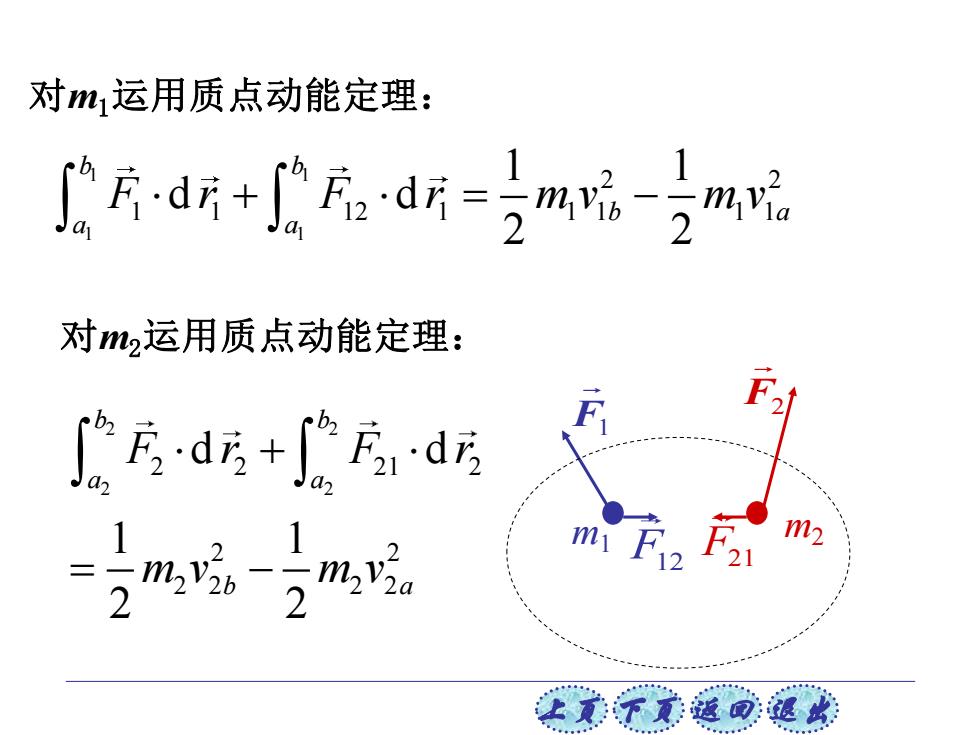
上页 下页 返回 退出 对m1运用质点动能定理: 对m2运用质点动能定理: 1 1 1 1 2 2 1 1 12 1 1 1 1 1 1 1 d d 2 2 b b b a a a F r F r m v m v + = − 2 2 2 2 2 2 21 2 2 2 2 2 2 2 d d 1 1 2 2 b b a a b a F r F r m v m v + = − F1 F2 F12 F21 m1 m2

作为系统考虑时,得到 疗d+店d房+京dr+元d厅 =兮m店+)一(m呢+) A外+A内=Ekb-Ea=AE 质点系动能定理:所有外力与所有内力对质点系 作功之和等于质点系总动能的增量。 推广:上述结论适用多个质点
上页 下页 返回 退出 作为系统考虑时,得到 推广:上述结论适用多个质点。 质点系动能定理:所有外力与所有内力对质点系 作功之和等于质点系总动能的增量。 1 2 1 1 1 2 1 1 1 1 2 2 12 1 21 2 2 2 2 2 1 1 2 2 1 1 2 2 d d d d 1 1 1 1 ( ) ( ) 2 2 2 2 b b b b a a a a b b a a F r F r F r F r m v m v m v m v + + + = + − + A A E E E 外 + = − = 内 k k k b a

二、质点系功能原理 A+A=AEs 因为对系统的内力来说,它们有保守内力和非保守 内力之分,所以内力的功也分为保守内力的功 和非 保守内力的功 4a A=Ac+A又A。=-△E 所以 A+A:=△E+△E,=△E 系统的功能原理:当系统从状态1变化到状态2时, 它的机械能的增量等于外力的功与非保守内力的功的 总和,这个结论叫做系统的功能原理。 让美觉返司退
上页 下页 返回 退出 因为对系统的内力来说,它们有保守内力和非保守 内力之分,所以内力的功也分为保守内力的功 和非 保守内力的功 。 Aic Aid A A A i ic id = + A E ic p = − A A E E E e id k p + = + = A A E e i k + = 二、质点系功能原理 系统的功能原理:当系统从状态1变化到状态2时, 它的机械能的增量等于外力的功与非保守内力的功的 总和,这个结论叫做系统的功能原理。 又 所以
例题2-16 一汽车的速度y=36km/h,驶至一斜率为 0.010的斜坡时,关闭油门。设车与路面间的摩擦阻 力为车重G的0.05倍,问汽车能冲上斜坡多远? 解:解法一,根据动能定理,取汽车为研究对象, 受力如图所示。 -F·s-Gs sin a=0- 2 上式说明,汽车上坡时, 动能一部分消耗于反抗摩 擦力作功,一部分消耗于 反抗重力作功。因 FFFN产uGu所以 UG S+Gssina=- (2)
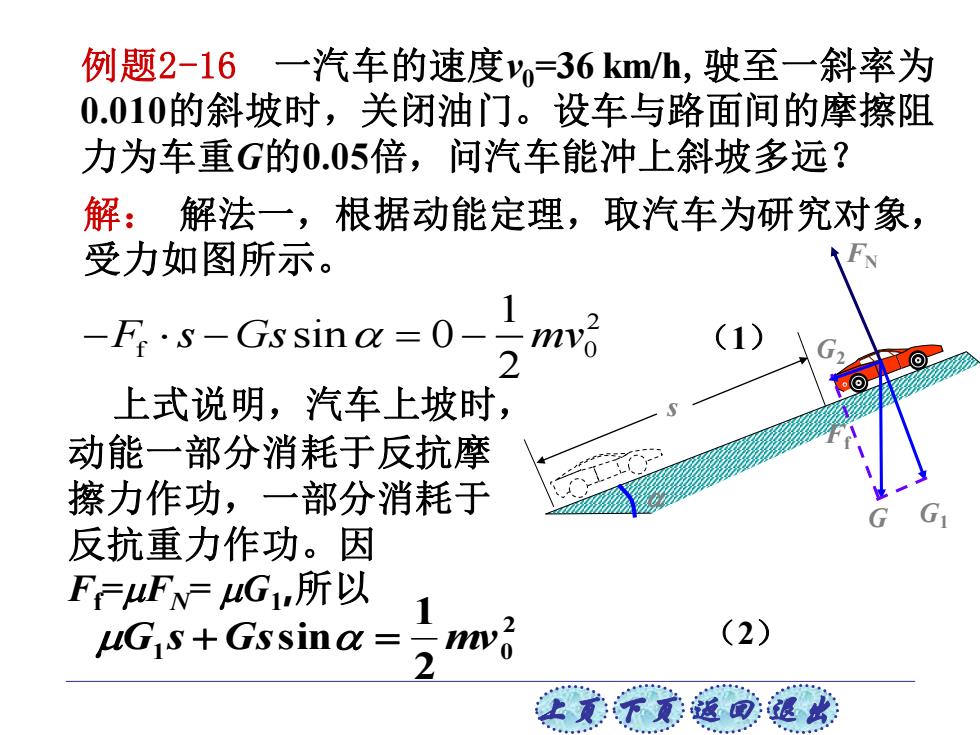
上页 下页 返回 退出 解: 解法一,根据动能定理,取汽车为研究对象, 受力如图所示。 例题2-16 一汽车的速度v0=36 km/h,驶至一斜率为 0.010的斜坡时,关闭油门。设车与路面间的摩擦阻 力为车重G的0.05倍,问汽车能冲上斜坡多远? 上式说明,汽车上坡时, 动能一部分消耗于反抗摩 擦力作功,一部分消耗于 反抗重力作功。因 Ff=FN= G1 ,所以 2 f 0 1 sin 0 2 − − = − F s Gs mv (1) 2 1 0 2 1 G s + Gssin = mv (2) s G G1 G2 FN Ff

按题意,tano-0.010,表示斜坡与水平面的夹角 很小,所以sin ar tan a,G1≈G,并因G=mg,上式 可化成 1 ugs+gs tan a=vo (3) 喝 或 S 2g(u+tana) 代入已知数值得 5=85m 解法二:根据功能原理,有 -F·s=0+Gssina)-(5m哈+0) 即GS= Imv-Gssin (4) 代入已知数值亦得 s=85m 江觉子觉返司退欢
上页 下页 返回 退出 按题意,tan =0.010,表示斜坡与水平面的夹角 很小,所以sin ≈ tan ,G1 ≈ G,并因G=mg,上式 可化成 2 0 1 tan 2 gs gs v + = (3) s = 85 m 2 0 2 ( tan ) v s g = + 或 代入已知数值得 解法二:根据功能原理,有 2 f 0 1 0 sin ) ( 0) 2 − + − + F s Gs mv =( 即 sin (4) 2 1 2 Gs = mv 0 −Gs 代入已知数值亦得 s = 85 m

例题2-17在图中,一个质量=2kg的物体从静止开 始,沿四分之一的圆周从A滑到B,已知圆的半径 R=4m,设物体在B处的速度=6m/s,求在下滑过程中, 摩擦力所作的功。 解:解法一,根据功的定义,以m为研究对象,受力 分析. mg cos0-F:ma,=m d dv 则F=mg cos0-m dr Aa=-∫Fds =-mg cos0Rde+fmvdy =-mgR+mv?
上页 下页 返回 退出 例题2-17 在图中,一个质量m=2kg的物体从静止开 始,沿四分之一的圆周从A滑到B,已知圆的半径 R=4m,设物体在B处的速度v=6m/s,求在下滑过程中, 摩擦力所作的功。 FN G Ff O R A B v f d cos d v F mg m t = − f t d cos d v mg F ma m t − = = 则 解:解法一,根据功的定义,以m为研究对象,受力 分析. f A F s = − d 阻 90 0 0 cos d d v mg R mv v = − + 1 2 2 = − + mgR mv

解法二,根据动能定理,对物体受力分析,只有重力 和摩擦力作功, ∫mg cos0ds+A组=号mv2 解法三,根据功能原理,以物体和地球为研究对象 A=0,An=A阻 4=A5+AS,=号m2-mgR 代入已知数字得 A=mm2-mgR=-42.4 负号表示摩擦力对物体作负功,即物体反抗摩擦力 作功42.4J。 让美子觉返司退此
上页 下页 返回 退出 解法二,根据动能定理,对物体受力分析,只有重力 和摩擦力作功, 1 2 cos d 2 mg s A mv + = 阻 90 2 0 1 cos d 2 A mv mg R = − 阻 1 2 2 = − mv mgR 解法三,根据功能原理,以物体和地球为研究对象 Ae = 0 in , A A = 阻 A E E 阻 = + k p 1 2 2 = − mv mgR 1 2 42.4J 2 代入已知数字得 A mv mgR = − = − 负号表示摩擦力对物体作负功,即物体反抗摩擦力 作功42.4 J

三、机械能守恒定律 机械能守恒定律:如果一个系统内只有保守内力 做功,或者非保守内力与外力的总功为零,则系统 内各物体的动能和势能可以互相转换,但机械能的 总值保持不变。这一结论称为机械能守恒定律。 条件A+Aa=0 定律Ea+Ea=Ekb+Eo 或E=Ek十E。=常量 或Ekb一Eka=Epa-Epb 让意子意通回退此
上页 下页 返回 退出 机械能守恒定律:如果一个系统内只有保守内力 做功,或者非保守内力与外力的总功为零,则系统 内各物体的动能和势能可以互相转换,但机械能的 总值保持不变。这一结论称为机械能守恒定律。 或 E E E = + = k p 常量 或 E E E E kb ka pa pb −=− 条件 e id A A + = 0 定律 E E E E ka pa kb pb + = + 三、机械能守恒定律

四、能量守恒定律 一个孤立系统经历任何变化时,该系统的所有能量 的总和是不变的,能量只能从一种形式变化为另外一 种形式,或从系统内一个物体传给另一个物体。这就 是普遍的能量守恒定律。 例题2-18起重机用钢丝绳吊运一质量为m的物体, 以速度作匀速下降,如图所示。当起重机突然刹车 时,物体因惯性进行下降,问使钢丝绳再有多少微小 的伸长?((设钢丝绳的劲度系数为k,钢丝绳的重力忽 略不计)。这样突然刹车后,钢丝绳所受的最大拉力 将有多大? 江美子觉返司退此
上页 下页 返回 退出 一个孤立系统经历任何变化时,该系统的所有能量 的总和是不变的,能量只能从一种形式变化为另外一 种形式,或从系统内一个物体传给另一个物体。这就 是普遍的能量守恒定律。 四、能量守恒定律 例题2-18 起重机用钢丝绳吊运一质量为m 的物体, 以速度v0作匀速下降,如图所示。当起重机突然刹车 时,物体因惯性进行下降,问使钢丝绳再有多少微小 的伸长?(设钢丝绳的劲度系数为k,钢丝绳的重力忽 略不计)。这样突然刹车后,钢丝绳所受的最大拉力 将有多大?