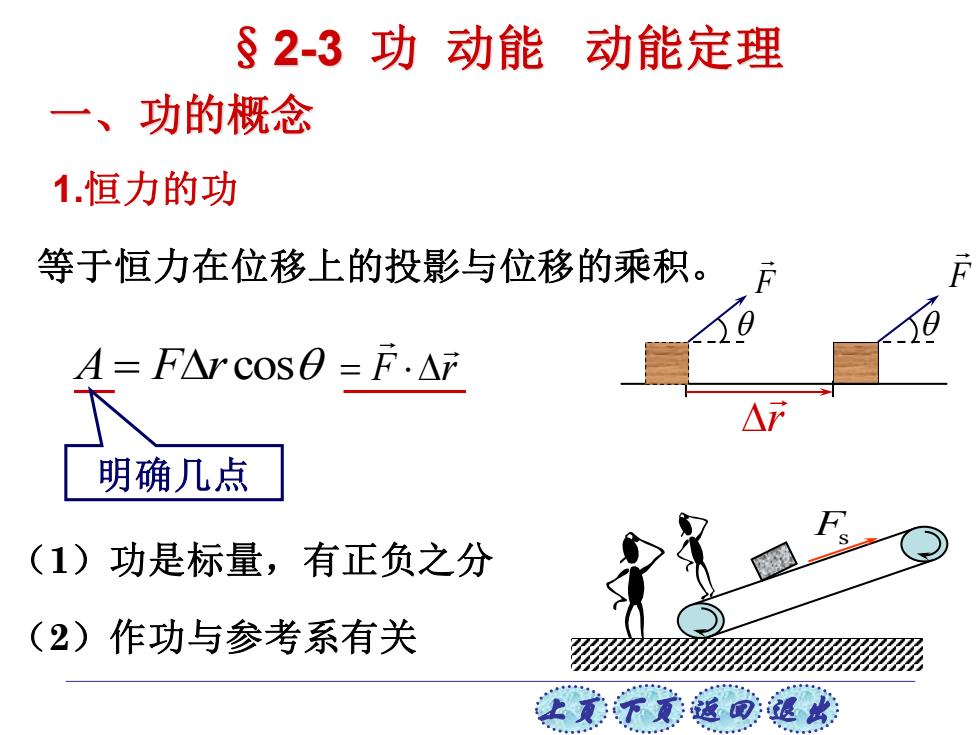
§2-3功动能 动能定理 一、功的概念 1.恒力的功 等于恒力在位移上的投影与位移的乘积。 A=FAr cos0=F.△F 明确几点 (1)功是标量,有正负之分 (2)作功与参考系有关 王美下美菠回:退收
上页 下页 返回 退出 F 等于恒力在位移上的投影与位移的乘积。 r A = Fr cos F r = F (1)功是标量,有正负之分 (2)作功与参考系有关 一、功的概念 1.恒力的功 明确几点 Fs §2-3 功 动能 动能定理

2.变力的功 物体在变力的作用 辉堡屦松A个金 下从运动到b。 怎样计算这个力 的功呢? 采用微元分割法 让意了意返可退收
上页 下页 返回 退出 b a 物体在变力的作用 下从a运动到b。 怎样计算这个力 的功呢? 采用微元分割法 2.变力的功
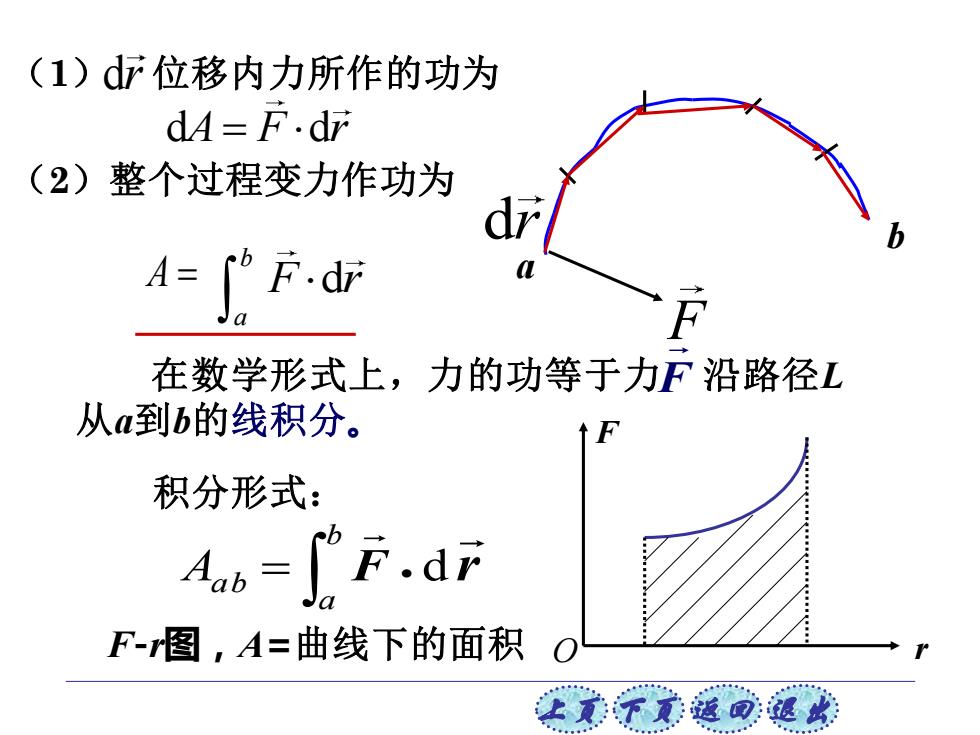
(1)d位移内力所作的功为 dA=F.dr (2)整个过程变力作功为 1=心F. 在数学形式上,力的功等于力F沿路径L 从a到b的线积分。 积分形式: oo= F-图,A=曲线下的面积 让美下元道司退此
上页 下页 返回 退出 F b a dr (1) dr 位移内力所作的功为 d d A F r = F r d (2)整个过程变力作功为 b a A = 积分形式: F r • d = b a Aa b 在数学形式上,力的功等于力 沿路径L 从a到b的线积分。 F F-r图,A=曲线下的面积 F O r

直角坐标系: 受力 F=Fi+Fj+Fk (N) 元位移 dr =dxi +dyj+dzk (m) 元功 dA=Fdx+F,dy+Fdz 总功 Ab=JFdr+∫Fdy+∫Fd正 自然坐标系: 46=∫rds F.d=(Fe+F).dse=Fds 让意子意通回退块
上页 下页 返回 退出 直角坐标系: d d d d A F x F y F z = + + x y z d d d b b b a a a x y z ab x y z x y z A F x F y F z = + + 总功 (N) F F i F j F k = + + x y z d d d d (m) r xi yj zk = + + 元功 受力 元位移 自然坐标系: t d b a s ab s A F s = t t n n t F r F e F e se = + d ( ) d t = F s d

3.合力的功 A6=心F.d=(+E++F)d 4.功率 =A+4++4,=∑4 (1)平均功率P= △A △t △A d (2)功率P=lim 0△t di 恒力的功率: P=F.v d1 P =京可 dt dt 江美觉返司退
上页 下页 返回 退出 (1)平均功率 t A P = (2) 功率 d d A P t = 恒力的功率: t A P t = →0 lim d d A t = d d r F t = F v = P F v = 1 2 d ( ) d b b ab n a a A F r F F F r = = + ++ 1 2 n n i i = + + + = A A A A 3.合力的功 4.功 率

二、能量 能量是各种运动形式的一般量度,是物体状 态的单值函数,反映物体作功的本领。 三、动能定理 根据功的积分形式 Ab=F.dF=∫Fds=∫ma,ds dv -S'm ds =mvdv dt 1 定义质点的动能为 Ek 2 让意不意道可退此
上页 下页 返回 退出 能量是各种运动形式的一般量度,是物体状 态的单值函数,反映物体作功的本领。 二、能量 三、动能定理 根据功的积分形式 = b Aab a F r d t d b a = ma s 2 2 2 1 2 1 = m vb − m va s t v m b a d d d = t d b a = F s b a d v v = mv v 2 k 1 2 定义质点的动能为 E mv =

动能定理:合外力对质点所作的功等于质点动 能的增量。 Aab =Ekh-Eka =AEk 几点注意: a.合力作正功时,质点动能增大;反之,质 点动能减小。 b.动能的量值与参考系有关。 c动能定理只适用于惯性系。 d功是一个过程量,而动能是一个状态量, 它们之间仅仅是一个等量关系。 江美觉返司退
上页 下页 返回 退出 A E E E ab b a = − = k k k 动能定理:合外力对质点所作的功等于质点动 能的增量。 a.合力作正功时,质点动能增大;反之,质 点动能减小。 d.功是一个过程量,而动能是一个状态量, 它们之间仅仅是一个等量关系。 b.动能的量值与参考系有关。 c.动能定理只适用于惯性系。 几点注意:
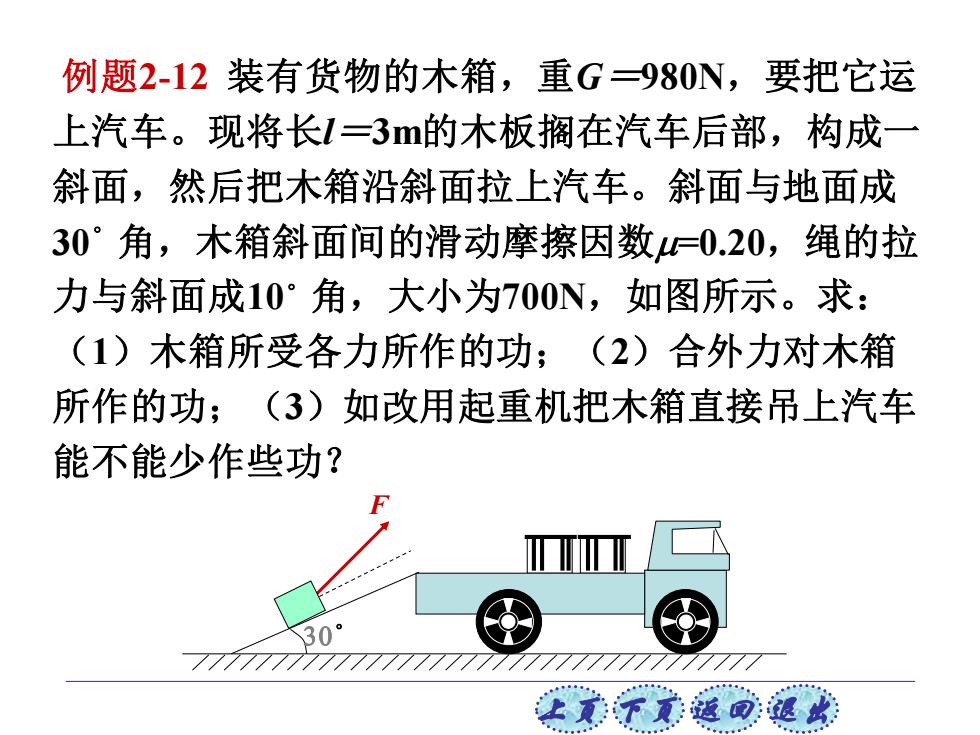
例题2-12装有货物的木箱,重G=980N,要把它运 上汽车。现将长1=3m的木板搁在汽车后部,构成一 斜面,然后把木箱沿斜面拉上汽车。斜面与地面成 30°角,木箱斜面间的滑动摩擦因数=0.20,绳的拉 力与斜面成10°角,大小为700N,如图所示。求: (1)木箱所受各力所作的功;(2)合外力对木箱 所作的功;(3)如改用起重机把木箱直接吊上汽车 能不能少作些功? 30 上套不意返回退此
上页 下页 返回 退出 例题2-12 装有货物的木箱,重G=980N,要把它运 上汽车。现将长l=3m的木板搁在汽车后部,构成一 斜面,然后把木箱沿斜面拉上汽车。斜面与地面成 30。角,木箱斜面间的滑动摩擦因数=0.20,绳的拉 力与斜面成10。角,大小为700N,如图所示。求: (1)木箱所受各力所作的功;(2)合外力对木箱 所作的功;(3)如改用起重机把木箱直接吊上汽车 能不能少作些功? 30。 F

解:木箱所受的力如图所示 (1)拉力F所作的功A1 A=FI cos10°=2.07×103J 30 重力G所作的功A2 4,=G1c0s(180°-60°)=-1.47×103J 正压力F所作的功A3 4=FIcos90°=0 摩擦力F所作的功A4 分析木箱的受力,由于木箱在垂直于斜面方向上 没有运动,根据牛顿第二定律得 让美觉返司退
上页 下页 返回 退出 解:木箱所受的力如图所示 (1)拉力F 所作的功A1 3 1 A Fl = = cos10 2.07 10 J 重力G所作的功A2 3 2 A Gl = = cos 180 60 1.47 10 J ( - ) - FN 10° 30° F G Ff 正压力 FN 所作的功A3 3 N A F l = = cos90 0 摩擦力Ff所作的功A4 分析木箱的受力,由于木箱在垂直于斜面方向上 没有运动,根据牛顿第二定律得

F+Fsin10°-Gcos30°=0 F=Gcos30°-Fsin10°=727N 由此可求得摩擦力F=uF=145N A,=F:Icos180°=-435J (2)根据合力所作功等于各分力功的代数和,算 出合力所作的功 4=4+4+4+4=165J (3)如改用起重机把木箱吊上汽车,这时所用拉力 F'至少要等于重力G。在这个拉力的作用下,木 箱移动的竖直距离是1sin30°。因此拉力所作的功 A'=Flsin30°=1.47×103J 让贰子元道同退此
上页 下页 返回 退出 N F F G + − = sin10 cos30 0 N F G F = cos30 sin10 727N - = 由此可求得摩擦力 f N F F = = 145N 4 f A F l = cos180 435J = − (2)根据合力所作功等于各分力功的代数和,算 出合力所作的功 1 2 3 4 A A A A A = + + + =165J (3)如改用起重机把木箱吊上汽车,这时所用拉力 至少要等于重力 。在这个拉力的作用下,木 箱移动的竖直距离是 。因此拉力所作的功 为 F G lsin 30 3 A Fl = = sin30 1.47 10 J