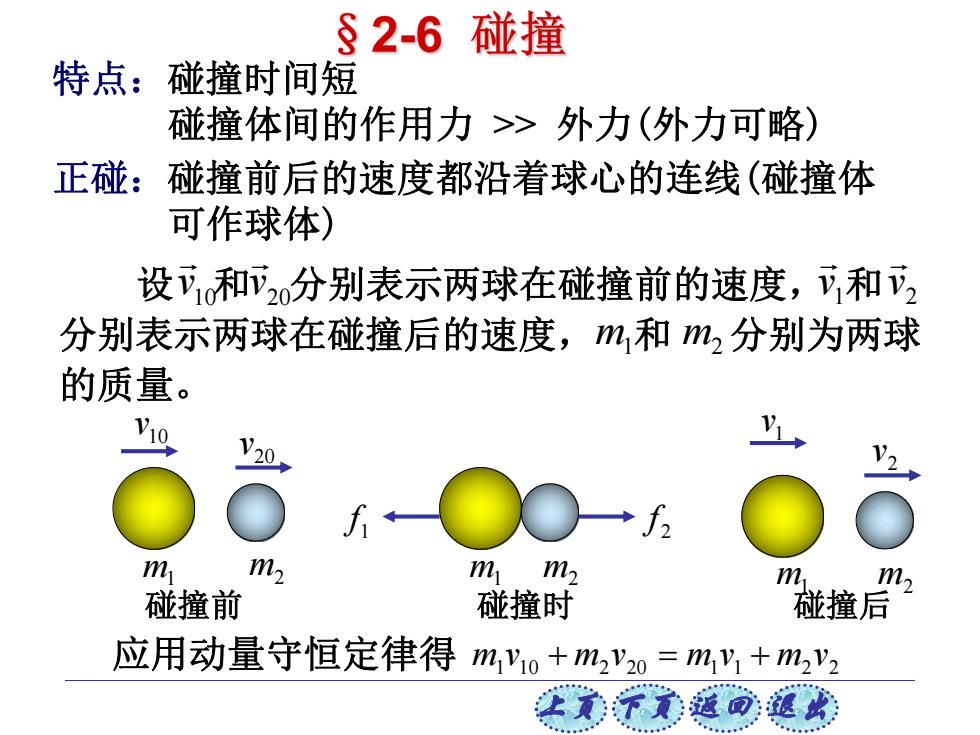
§2-6碰撞 特点:碰撞时间 碰撞体间的作用力>外力(外力可略) 正碰:碰撞前后的速度都沿着球心的连线(碰撞体 可作球体) 设和币2分别表示两球在碰撞前的速度,和 分别表示两球在碰撞后的速度,m,和m2分别为两球 的质量。 f →f 1m1 m 1m1m2 m. m2 碰撞前 碰撞时 碰撞后 应用动量守恒定律得m,y1o+m2y20=my+m2y2 买元子元道可越埃
上页 下页 返回 退出 正碰:碰撞前后的速度都沿着球心的连线(碰撞体 可作球体) 特点:碰撞时间短 碰撞体间的作用力 >> 外力(外力可略) 10 v 20 v 1 f 2 f 1 v 2 v m1 m2 m1 m1 m2 m2 碰撞前 碰撞时 碰撞后 设 和 分别表示两球在碰撞前的速度, 和 分别表示两球在碰撞后的速度, 和 分别为两球 的质量。 10 v 20 v m1 2 v m2 1 v 应用动量守恒定律得 1 10 2 20 1 1 2 2 m v m v m v m v

牛顿的碰撞定律:碰撞后两球的分离速 度(y2-y),与碰撞前两球的接近速度(y。-y)成正比 比值由两球的材料性质决定。 恢复系数 V2-V1 e y10-V20 =0,碰撞后两球以同一速度运动,并不分开, 称为完全非弹性碰撞。 e=1,分离速度等于接近速度,称为完全弹性 碰撞。 0≤e<1,机械能有损失的碰撞叫做非弹性碰撞。 让元了文返可速此
上页 下页 返回 退出 10 20 2 1 v v v v e 牛 顿 的 碰 撞 定 律 : 碰 撞 后 两 球 的 分 离 速 度 ,与碰撞前两球的接近速度 成正比 比值由两球的材料性质决定。 ( ) 2 1 v v ( ) 10 20 v v ,碰撞后两球以同一速度运动,并不分开, 称为完全非弹性碰撞。 e 0 0 e 1 ,机械能有损失的碰撞叫做非弹性碰撞。 ,分离速度等于接近速度,称为完全弹性 碰撞。 e 1 恢复系数
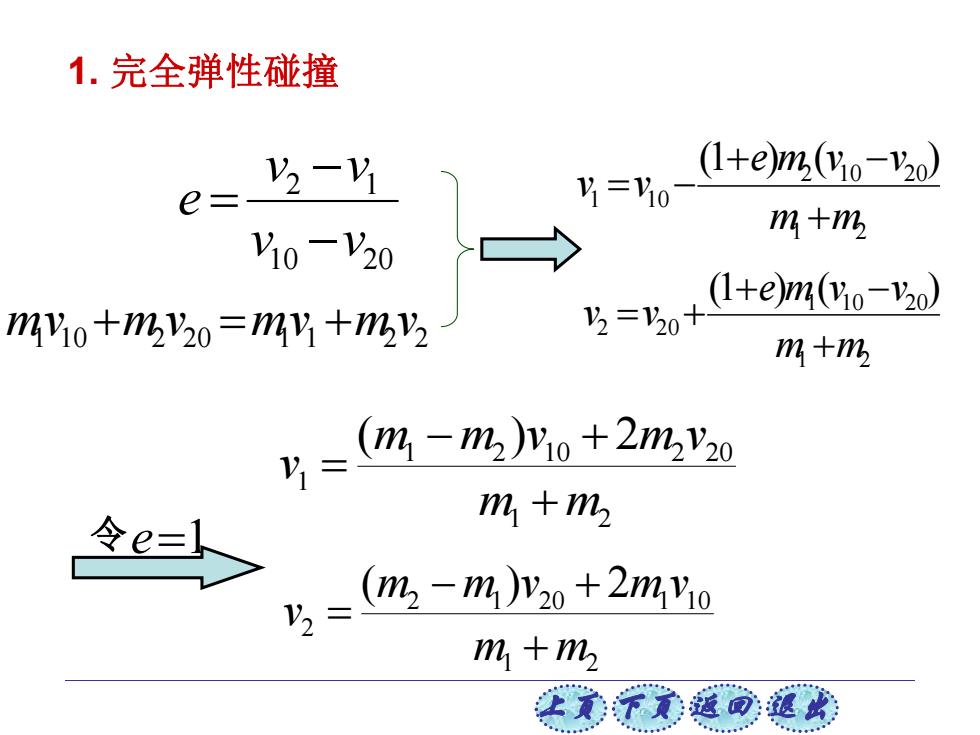
1.完全弹性碰撞 (1+e)m(Yo-2o) e= 2- Y=1Y0 y10-V20 m+% > mvo+mv2o=my+mv 3=5+0+em43-5 m+% y=0m-%M+230 m1+m2 (m2-m)y20+2mYo V,= m +m
上页 下页 返回 退出 1 2 2 10 20 1 10 (1 ) ( ) m m e m v v v v 1 2 1 10 20 2 20 (1 ) ( ) m m e m v v v v 10 20 2 1 v v v v e 1 10 2 20 1 1 2 2 mv mv mv mv 令e1 1 2 1 2 10 2 20 1 ( ) 2 m m m m v m v v 1 2 2 1 20 1 10 2 ( ) 2 m m m m v mv v 1. 完全弹性碰撞

讨论: (1) 设m1=m2,得1=V20,2=V10’两 球经过碰撞将交换彼此的速度。 (2)设m1丰m2,质量为m2的物体在碰撞 前静止不动,即V20=0 y=所-%ho V2= 2m1'1o m1+m2 m1+m2 让元了滋可:速线
上页 下页 返回 退出 (1)设 ,得 , 两 球经过碰撞将交换彼此的速度。 m1 m2 1 20 2 10 v v ,v v (2)设 ,质量为 的物体在碰撞 前静止不动,即 m1 m2 m2 v20 0 1 2 1 2 10 1 ( ) m m m m v v 1 2 1 10 2 2 m m m v v 讨论:

(3)如果m2>>m1 m-≈-1, 2m 小球碰静 ≈0 止的大球 m +m m,+m2 (m-m2)vio m +m 2= 2mvio %≈0 m +m 质量极大并且静止的物体,经碰撞后,几乎仍静 止不动,而质量极小的物体在碰撞前后的速度方向相 反,大小几乎不变。 生美子美返回蕴
上页 下页 返回 退出 (3)如果 m2 m1 1 2 1 2 1, m m m m 0 2 1 2 1 m m m 1 10 v v 0 v2 质量极大并且静止的物体,经碰撞后,几乎仍静 止不动,而质量极小的物体在碰撞前后的速度方向相 反,大小几乎不变。 1 2 1 2 10 1 ( ) m m m m v v 1 2 1 10 2 2 m m mv v 小球碰静 止的大球

2.完全非弹性碰撞 在完全非弹性碰撞中e=0 (1+e)m2(1o-y20) V=VO- m1+m2 5=2++em。-2 m,+m2 mvio m2v20 y=V2= m1+m2 让元了滋可速线
上页 下页 返回 退出 在完全非弹性碰撞中 e 0 2 10 20 1 10 1 2 (1 e)m (v v ) v v m m 1 10 20 2 20 1 2 (1 e)m (v v ) v v m m 1 10 2 20 1 2 1 2 m v m v v v m m 2. 完全非弹性碰撞

3.碰撞中的力和能 设在两球相碰撞的问题中,碰撞接触时间极短, 用△t表示,把动量定理应用于质量为m,的小球得 F m2v2-m2V20 △t m,m,(1+e(o-0) =y+0+emo-2 (m+m2)△ m +m 表明:力的大小和两物体相遇前的接近速度成 正比,而和接触时间成反比。力的大小与接触物体 的质量和材料有关。 士了元送可速瑞
上页 下页 返回 退出 m2 2 2 20 v m v F t 1 2 1 10 20 2 20 (1 ) ( ) m m e m v v v v 设在两球相碰撞的问题中,碰撞接触时间极短, 用 t 表示,把动量定理应用于质量为 m 2 的小球得 1 2 10 20 1 2 (1 )( ) ( ) m m e v v F m m t 表明:力的大小和两物体相遇前的接近速度成 正比,而和接触时间成反比。力的大小与接触物体 的质量和材料有关。 3. 碰撞中的力和能

(1+e)m(4o-2o) y=Vo m+% 5=n+1+emo-) m1+m2 系统损失的机械能 2 m +m 让美了元滋可速此
上页 下页 返回 退出 2 10 20 1 2 2 1 2 (1 ) ( ) 2 1 v v m m mm E e 1 2 2 10 20 1 10 (1 ) ( ) m m e m v v v v 1 2 1 10 20 2 20 (1 ) ( ) m m e m v v v v 系统损失的机械能
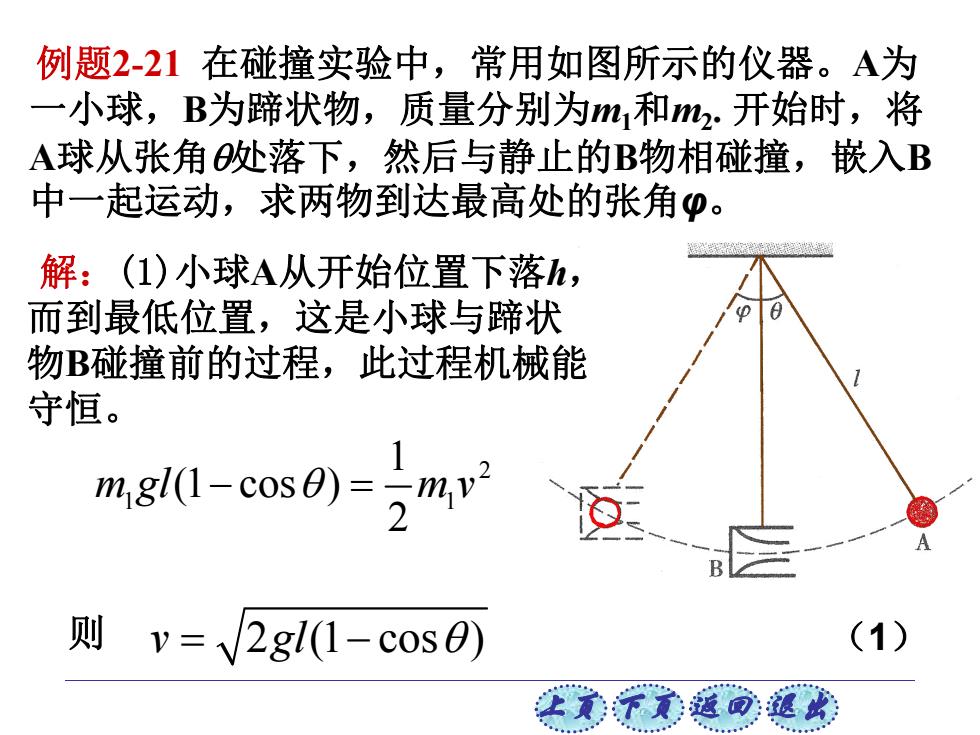
例题2-21在碰撞实验中,常用如图所示的仪器。A为 一小球,B为蹄状物,质量分别为m,和m2.开始时,将 A球从张角处落下,然后与静止的B物相碰撞,嵌入B 中一起运动,求两物到达最高处的张角p。 解:(1)小球A从开始位置下落h, 而到最低位置,这是小球与蹄状 物B碰撞前的过程,此过程机械能 守恒。 mw-cos)-克mr 则v=V2gl(1-cos0) (1) 士家了文返可:道此
上页 下页 返回 退出 则 例题2-21 在碰撞实验中,常用如图所示的仪器。A为 一小球,B为蹄状物,质量分别为m1和m2 . 开始时,将 A球从张角处落下,然后与静止的B物相碰撞,嵌入B 中一起运动,求两物到达最高处的张角φ。 解:(1)小球A从开始位置下落h, 而到最低位置,这是小球与蹄状 物B碰撞前的过程,此过程机械能 守恒。 2 1 1 1 (1 cos ) 2 m gl m v v 2gl(1 cos) (1)

(2)当小球与蹄状物碰撞时,两物作完全非弹性碰 撞,动量守恒 mv=(m +m)v' (2) (3)小球与蹄状物开始运动后,在这过程中机械能 守恒定律,即 m+m%n2=(m+mlgl-cs网 1 则 v=2gl(1-cosp) (3) 从(1)、(2)和(3)三式消去和y',可得 c0s0=1 m (1-cos0) m1+m2 利用这种碰撞实验,可以验证动量守恒与机械能守 恒定律。 让元了滋可速线
上页 下页 返回 退出 (2)当小球与蹄状物碰撞时,两物作完全非弹性碰 撞,动量守恒 1 1 2 m v (m m )v 2 1 2 1 2 1 ( ) ' ( ) (1 cos ) 2 m m v m m gl (3)小球与蹄状物开始运动后,在这过程中机械能 守恒定律,即 v' 2gl(1cos) 从(1)、(2)和(3)三式消去v和v′ ,可得 利用这种碰撞实验,可以验证动量守恒与机械能守 恒定律。 2 1 1 2 cos 1 (1 cos ) m m m 则 (2) (3)