《普通物理学》课程教学资源（PPT课件）第三章 刚体和流体的运动 3-5 进动

*§3-5进动 进动：高速旋转的物体，其自转轴绕另一个轴 转动的现象。 正意子元道回退此

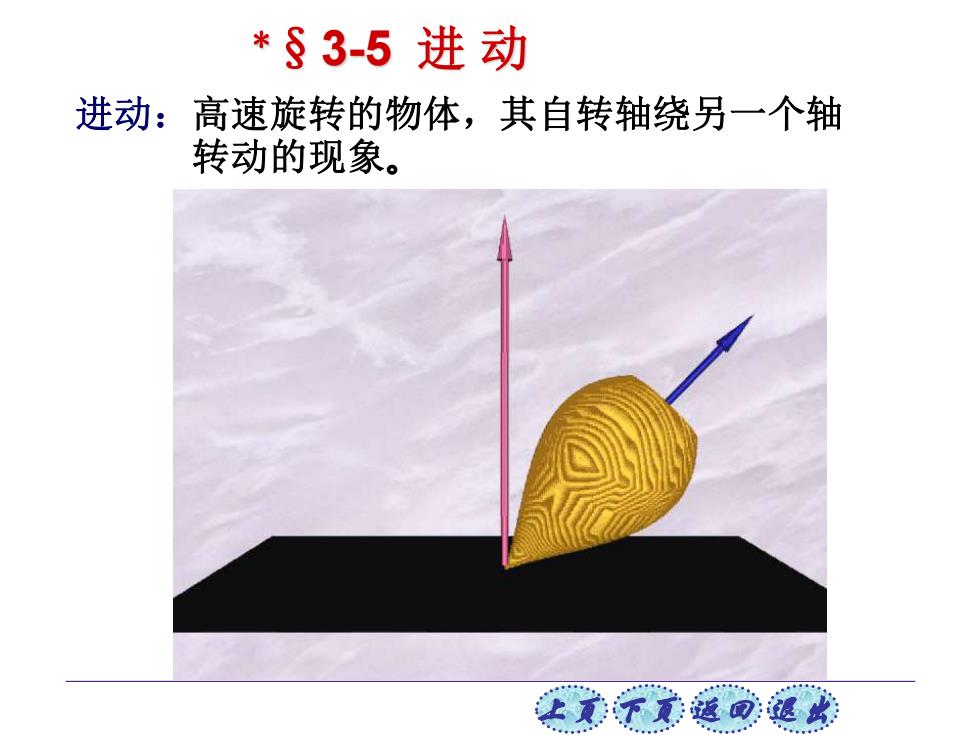
上页 下页 返回 退出 进动：高速旋转的物体，其自转轴绕另一个轴 转动的现象。 *§3-5 进 动

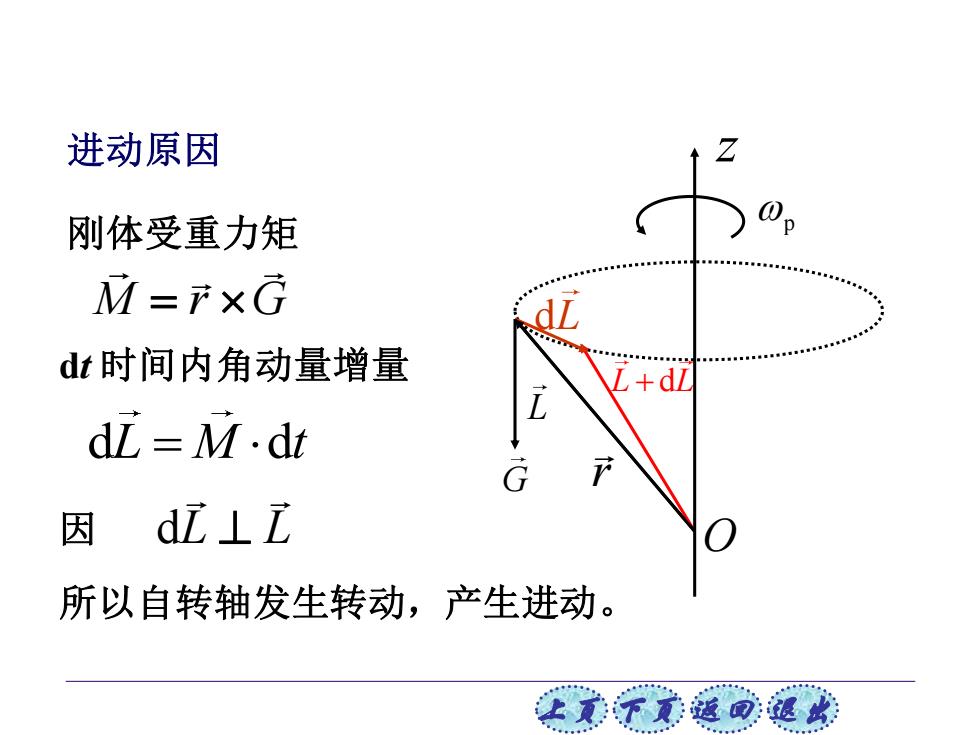
进动原因 刚体受重力矩 M=rxG dt时间内角动量增量 dl dI M.dt G 因 di⊥i 所以自转轴发生转动，产生进动。 让美觉返司退

上页 下页 返回 退出 进动原因 L L L + d dL p G M r G    =  刚体受重力矩 O z dt 时间内角动量增量 d d L M t =  因 L L   d ⊥ 所以自转轴发生转动，产生进动。 r 

实际上，转动中的进动现象相当于平动中的匀 速圆周运动，类比如下： 类比 刚体的进动 质点匀速圆周运动 具有角动量并在 具有动量并在 成因 外力矩作用下 外力作用下 共同点 两因素相互垂直 两因素相互垂直 角动量改变方向， 动量改变方向， 结果 自旋轴转动 作圆周运动

上页 下页 返回 退出 实际上，转动中的进动现象相当于平动中的匀 速圆周运动，类比如下： 刚体的进动 质点匀速圆周运动 成 因 具有角动量并在 外力矩作用下 具有动量并在 外力作用下 共同点 两因素相互垂直 两因素相互垂直 结果 角动量改变方向， 自旋轴转动 动量改变方向， 作圆周运动 类 比

用角动量定理研究进动 dL=Lsin ado Isin o =Jo sin a⑩ d⑩ 由角动量定理 dL Mdt 所以Mdt=Jo sin at 进动角速度 do M D dt JosinO 让美觉返司退

上页 下页 返回 退出 用角动量定理研究进动 L  L L + d dL Lsin d p G O z dL = Lsind = Jsind 由角动量定理 dL = Mdt 所以 p d dt   = Jsin M = 进动角速度 Mdt = Jsindt

由此可知，进动角速度0。与外力矩成正比，与陀 螺自转的角动量成反比。因此，当陀螺自转角速度很大 时，进动角速度较小；而在陀螺自转角速度很小时，进 动角速度却增大。 回转效应在实践中有广泛的应用。例如，飞行中的子 弹或炮弹将受到空气阻力的作用，阻力的方向是逆着弹道 的，而且一般又不作用在子弹或炮弹的质心上，这样，阻 力对质心的力矩就可能使弹头翻转。为了保证弹头着地而 不翻转，常利用枪膛或炮筒中来复线的作用，使子弹或炮 弹绕自己的对称轴迅速旋转。由于回转效应，空气阻力的 力矩使子弹或炮弹的自转轴绕弹道方向进动，这样，子弹 或炮弹的自转轴就将与弹道方向始终保持不太大的偏离， 如图所示，再没有翻转的可能

上页 下页 返回 退出 回转效应在实践中有广泛的应用。例如，飞行中的子 弹或炮弹将受到空气阻力的作用，阻力的方向是逆着弹道 的，而且一般又不作用在子弹或炮弹的质心上，这样，阻 力对质心的力矩就可能使弹头翻转。为了保证弹头着地而 不翻转，常利用枪膛或炮筒中来复线的作用，使子弹或炮 弹绕自己的对称轴迅速旋转。由于回转效应，空气阻力的 力矩使子弹或炮弹的自转轴绕弹道方向进动，这样，子弹 或炮弹的自转轴就将与弹道方向始终保持不太大的偏离， 如图所示，再没有翻转的可能。 由此可知，进动角速度 与外力矩成正比，与陀 螺自转的角动量成反比。因此，当陀螺自转角速度很大 时，进动角速度较小；而在陀螺自转角速度很小时，进 动角速度却增大。 p

但是，任何事物都是一分为二的，回转效应有时也 引起有害的作用。例如，在轮船转弯时，由于回转效应， 涡轮机的轴承将受到附加的力，这在设计和使用中是必须 考虑的。 进动的概念在微观世界中也常用到。例如，原子中 的电子同时参与绕核运动与电子本身的自旋，都具有角动 量，在外磁场中，电子将以外磁场方向为轴线作进动。这 是从物质的电结构来说明物质磁性的理论依据。 上美下觉返可：退此

上页 下页 返回 退出 但是，任何事物都是一分为二的，回转效应有时也 引起有害的作用。例如，在轮船转弯时，由于回转效应， 涡轮机的轴承将受到附加的力，这在设计和使用中是必须 考虑的。 进动的概念在微观世界中也常用到。例如，原子中 的电子同时参与绕核运动与电子本身的自旋，都具有角动 量，在外磁场中，电子将以外磁场方向为轴线作进动。这 是从物质的电结构来说明物质磁性的理论依据

选择进入下一节 §3-0教学基本要求 §3-1刚体模型及其运动 §3-2力矩转动惯量定轴转动定律 §33定轴转动中的功能关系 §3-4定轴转动刚体的角动量定律和角动量守恒定律 *§3-5进动 *§3-6理想流体模型 定常流动伯努利方程 *§3-7牛顿力学的内在随机性混沌

上页 下页 返回 退出 选择进入下一节 §3-0 教学基本要求 §3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系 §3-4 定轴转动刚体的角动量定律和角动量守恒定律 *§3-5 进动 *§3-6 理想流体模型 定常流动 伯努利方程 *§3-7 牛顿力学的内在随机性 混沌