
§1-4牛顿运动定律 一、牛顿第一定律 任何物体都保持静止的或沿一条直线作匀速运动 状态,除非作用在它上面的力迫使它改变这种状态。 1.第一定律涉及了哪两个基本概念? 答:惯性和力。 2.第一定律定义了一个什么样的参考系? 答:惯性参考系。 3.一艘船在一个风平浪静的海面上匀速的航行,某人 站在船尾纵身向上一跃,问此人能否掉入海里?
上页 下页 返回 退出 一、牛顿第一定律 任何物体都保持静止的或沿一条直线作匀速运动 状态,除非作用在它上面的力迫使它改变这种状态。 1.第一定律涉及了哪两个基本概念? 答:惯性和力。 2.第一定律定义了一个什么样的参考系? 答:惯性参考系。 3.一艘船在一个风平浪静的海面上匀速的航行,某人 站在船尾纵身向上一跃,问此人能否掉入海里? §1-4 牛顿运动定律

二、牛顿第二定律 运动的变化与所加的合动力成正比,并且发生在 这合力所沿的直线的方向上。 1.第二定律中“运动”一词指什么? 答:质量与速度的乘积即动量。 2.怎样理解第二定律中“变化”一词? 答:对时间的变化率。 第二定律的数学表达式: d(mi)d(p) F =ma dt dt F d(mv) d dm d =m +V =m dt dt dt di ma
上页 下页 返回 退出 二、牛顿第二定律 运动的变化与所加的合动力成正比,并且发生在 这合力所沿的直线的方向上。 1.第二定律中“运动”一词指什么? 答:质量与速度的乘积即动量。 2.怎样理解第二定律中“变化”一词? 答:对时间的变化率。 第二定律的数学表达式: d( ) d mv F t = d( ) d p t = d( ) d mv F t = d d d d v m m v t t = + d d v m t = = ma F ma =

∑F=ma,=m dt 直角坐标系中:〈 ∑F=ma,=m v, ∑F:=ma =m dv dt F mai +ma,j+ma,k ∑F=ma,=m v 自然坐标系中: ∑=ma,=m F ma mae ma e 正觉不美返回退
上页 下页 返回 退出 d d y y y v F ma m t = = d d x x x v F ma m t = = d d z z z v F ma m t = = 直角坐标系中: t t 2 n n d d v F ma m t v F ma m = = = = 自然坐标系中: F ma i ma j ma k = + + x y z F ma ma e ma e = = + t t n n

三、牛顿第三定律 对于每一个作用,总有一 个相等的反作用与之相反:或F1 者说,两个物体对各自的对方 的作用总是相等的,而且指向 相反的方向。 牛顿第三定律的数学表达式: F2=-E 注意:1.作用力与反作用力同生同灭。 2.作用力与反作用分别作用于两个不同的物体, 各产生其效果。 3.作用力与反作用力性质相同。 士元子意返可退
上页 下页 返回 退出 三、牛顿第三定律 对于每一个作用,总有一 个相等的反作用与之相反;或 者说,两个物体对各自的对方 的作用总是相等的,而且指向 相反的方向。 2 1 牛顿第三定律的数学表达式: 注意:1.作用力与反作用力同生同灭。 2.作用力与反作用分别作用于两个不同的物体, 各产生其效果。 3.作用力与反作用力性质相同。 F21 F12 F F 12 21 = −

牛顿运动定律的几点说明: 1.牛定律只适用于惯性系; 2.牛顿第二定律只适用于质点或可看做质点的物体; 3.m尽是数值上等于合外力,它本身不是力。外力 改变时,它也同时改变,它们同时存在,同时改变, 同时消失。 江子元通回退此
上页 下页 返回 退出 牛顿运动定律的几点说明: 3. 只是数值上等于合外力,它本身不是力。外力 改变时,它也同时改变,它们同时存在,同时改变, 同时消失。 2.牛顿第二定律只适用于质点或可看做质点的物体; 1.牛顿定律只适用于惯性系; ma

四、牛顿定律应用举例 两类力学问趣:知繁泰》 桥梁是加速度a 解题步骤:十六字诀 隔离物体一一明确研究对象 具体分析 研究对象的运动情况和受力情 况,作出受力图 选定坐标 一一参考系、坐标系、正方向 建立方程一一 分量式 F mas =m dy:=m dt dr2 dv F=ma =m Fy may =m- dy二 d2y di dz2 dv. d2z F=ma=m F.ma.=m =m di d
上页 下页 返回 退出 四、牛顿定律应用举例 隔离物体——明确研究对象 具体分析——研究对象的运动情况和受力情 况,作出受力图 选定坐标——参考系、坐标系、正方向 建立方程——分量式 解题步骤:十六字诀 两类力学问题: 2 2 d d d d t x m t v F ma m x x = x = = 2 2 d d d d t y m t v F ma m y y = y = = 2 2 d d d d t z m t v F ma m z z = z = = t t d d v F ma m t = = 2 n n v F ma m = = •已知力求运动 •已知运动求力 a 桥梁是加速度
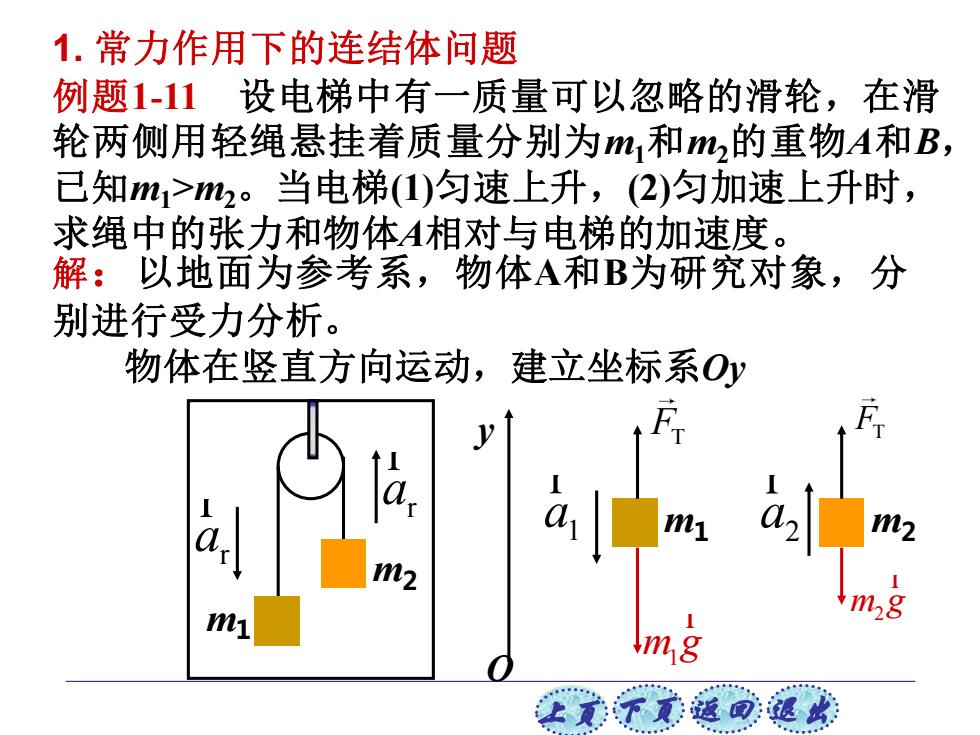
1.常力作用下的连结体问题 例题1-11设电梯中有一质量可以忽略的滑轮,在滑 轮两侧用轻绳悬挂着质量分别为m1和m,的重物A和B, 已知m1>m2。当电梯(1)匀速上升,(2)匀加速上升时, 求绳中的张力和物体A相对与电梯的加速度。 解:以地面为参考系,物体A和B为研究对象,分 别进行受力分析。 物体在竖直方向运动,建立坐标系Oy F dN m2 女元下觉通回退收
上页 下页 返回 退出 例题1-11 设电梯中有一质量可以忽略的滑轮,在滑 轮两侧用轻绳悬挂着质量分别为m1和m2的重物A和B, 已知m1>m2。当电梯(1)匀速上升,(2)匀加速上升时, 求绳中的张力和物体A相对与电梯的加速度。 r a r r a r m1 m2 O y 1 a r m1 2 a r m2 m g1 r m g2 r FT FT 解:以地面为参考系,物体A和B为研究对象,分 别进行受力分析。 物体在竖直方向运动,建立坐标系Oy 1. 常力作用下的连结体问题

(1)电梯匀速上升,物体对电梯的加速度等于它们对 地面的加速度。A的加速度为负,B的加速度为正, 根据牛顿第二定律,对A和B分别有 F-m8=-m, F-m28=m2a: 上两式消去FT,得 a= m,一m2g m1+m2 将代入上面任一式FT,得到 F= 2m,m2 m,+m2 上元不贰返可退
上页 下页 返回 退出 (1)电梯匀速上升,物体对电梯的加速度等于它们对 地面的加速度。A的加速度为负,B的加速度为正, 根据牛顿第二定律,对A和B分别有 F m g m a T 1 1 r − = − F m g m a T 2 2 r − = 上两式消去FT,得到 g m m m m a 1 2 1 2 r + − = 1 2 T 1 2 2m m F g m m = + 将ar代入上面任一式FT,得到

(2)电梯以加速度a上升时,A对地的加速度a,B 的对地的加速度为a+a,根据牛顿第二定律,对A 和B分别有 F-mg=m (a-a,) F-m28=m,(a+a) 解此方程组得到 a, m-2(a+g) m,+m2 F= 2m2(a+g) m1+m2 正下觉返同速
上页 下页 返回 退出 (2)电梯以加速度a上升时,A对地的加速度a-ar,B 的对地的加速度为a+ar,根据牛顿第二定律,对A 和B分别有 T 1 1 r F m g m a a − = − ( ) T 2 2 r F m g m a a − = + ( ) 解此方程组得到 ( ) 1 2 1 2 r a g m m m m a + + − = 1 2 T 1 2 2 ( ) m m F a g m m = + +

由(2)的结果,令=0,即得到的结果 a.= m1-m2 m1+m2 FT= 2m2 m+m 由(2)的结果,电梯加速下降时,<0,即得到 m-:(g-a) m,+m2 FT= 2mm2(g-a) m,+m2 上元不贰返可退
上页 下页 返回 退出 由(2)的结果,令a=0,即得到的结果 g m m m m a 1 2 1 2 r + − = 1 2 T 1 2 2m m F g m m = + 由(2)的结果,电梯加速下降时,a<0,即得到 ( ) 1 2 1 2 r g a m m m m a − + − = 1 2 T 1 2 2 ( ) m m F g a m m = − +