
§2-1质点系的内力和外力质心 质心运动定理 一、质点系的内力和外力 N个质点组成的系统,称为质点系。 内力:系统内部各质点间的相互作用力。 特点:成对出现;大小相等方向相反。 结论:质点系的内力之和为零∑内:=0 质点系F 外力:系统外部对质点系内部质点的作用力。 约定:系统内任一质点受力之和写成 外力之和) 疗+F内 内力之和 王美不元菠面:退收
上页 下页 返回 退出 N个质点组成的系统,称为质点系。 内力:系统内部各质点间的相互作用力。 质点系 特点:成对出现;大小相等方向相反。 结论:质点系的内力之和为零 外力: 系统外部对质点系内部质点的作用力。 F F内 ' F内 约定:系统内任一质点受力之和写成 外力之和 内力之和 一、 质点系的内力和外力 0 i F 内 = i F F i + 内i §2-1 质点系的内力和外力 质心 质心运动定理
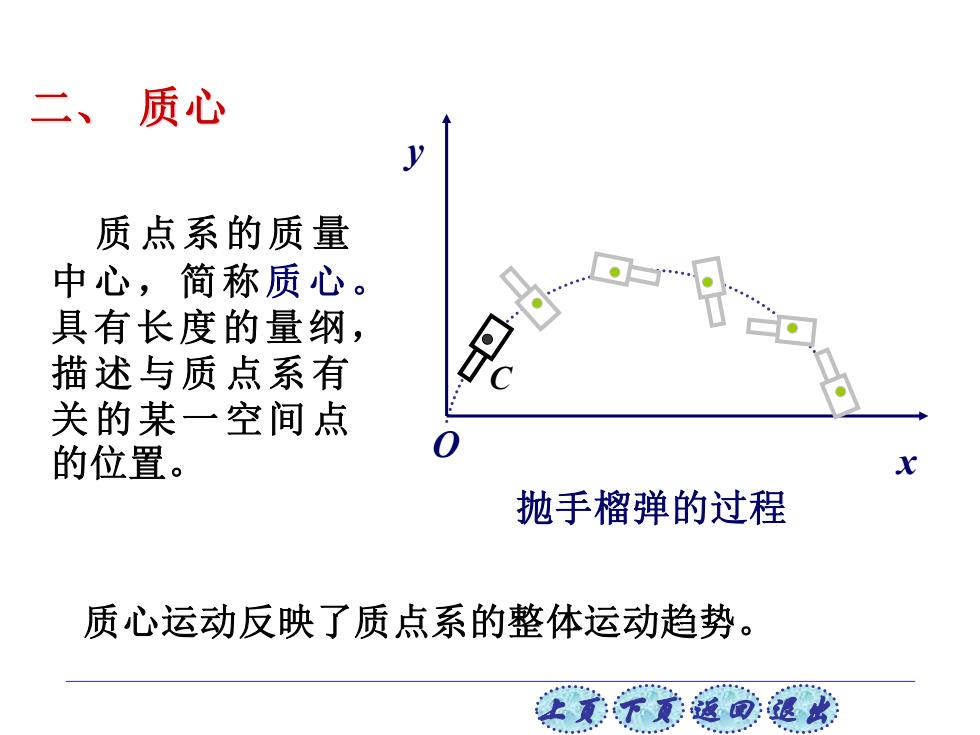
二、 质心 质点系的质量 中心,简称质心。 具有长度的量纲, 描述与质点系有 关的某一空间点 的位置。 抛手榴弹的过程 质心运动反映了质点系的整体运动趋势
上页 下页 返回 退出 抛手榴弹的过程 C O x y 质点系的质量 中心,简称质心。 具有长度的量纲, 描述与质点系有 关的某一空间点 的位置。 质心运动反映了质点系的整体运动趋势。 二、 质心
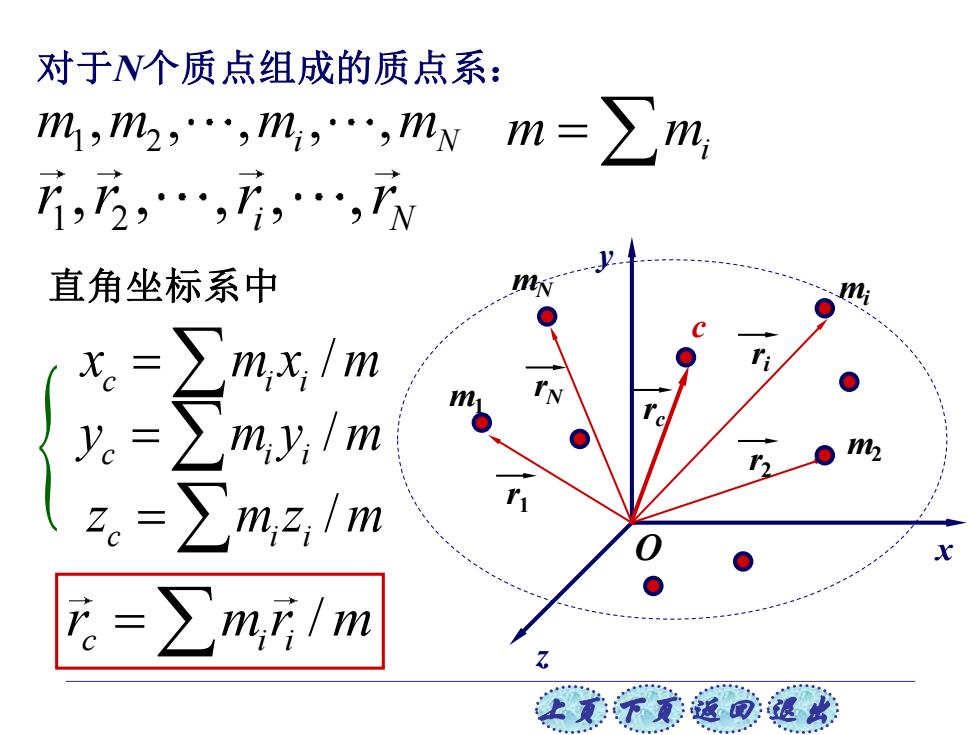
对于N个质点组成的质点系: m,m2,.,m,.,mvm=∑m i,.,., 直角坐标系中 mx;m yc= my;Im 元=∑,店/m 让美觉返司退
上页 下页 返回 退出 x z y O m2 r2 m1 r1 c rc mi ri rN mN 对于N个质点组成的质点系: 1 2 , , , , , m m m m i N 1 2 , , , , , i N r r r r / c i i x m x m = / c i i y m y m = / c i i z m z m = m m = i 直角坐标系中 / c i i r m r m =
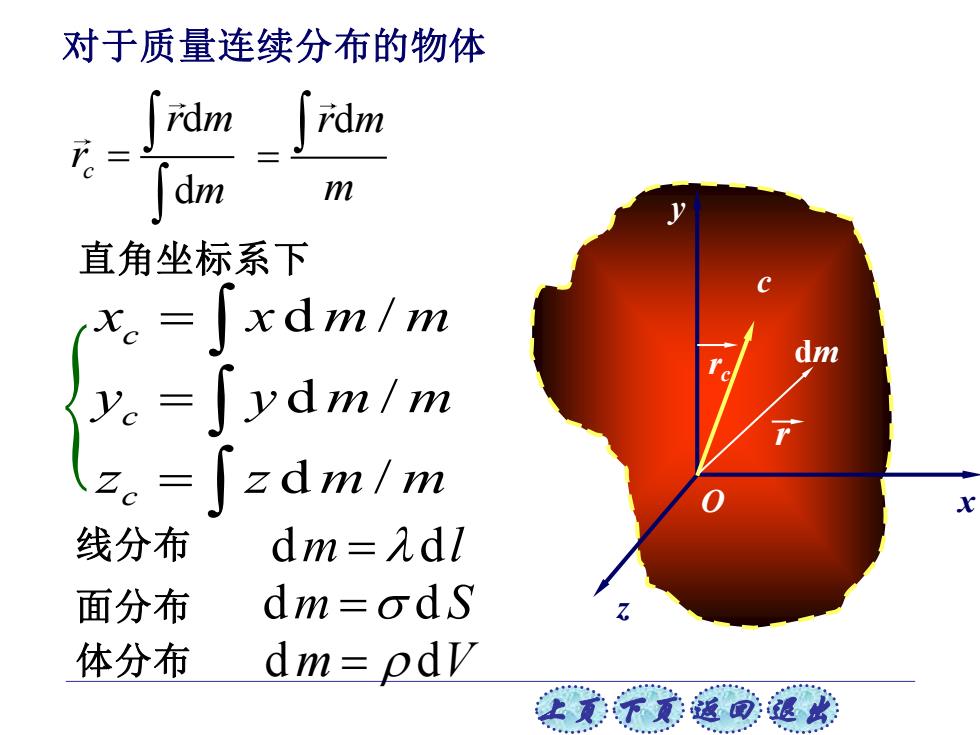
对于质量连续分布的物体 rdm dm m 1》 直角坐标系下 x=xdm/m y。=∫ydm/m z-[zdm/m 线分布 dm=λdl 面分布 dm=ods 体分布 dm=pdv 让美下觉返回退此
上页 下页 返回 退出 直角坐标系下 x z y O c rc dm r d d c r m r m = r md m = 面分布 体分布 线分布 dm = dl dm = d S dm = dV 对于质量连续分布的物体 d / c x x m m = d / c y y m m = d / c z z m m =

注意: Q质心的位矢与参考系的选取有关。 Q刚体的质心相对自身位置确定不变。 Q质量均匀的规则物体的质心在几何中心。 。质心与重心不一样,物体尺寸不十分大时,质心 与重心位置重合。 让美不文返藏:退
上页 下页 返回 退出 注意: 质心的位矢与参考系的选取有关。 刚体的质心相对自身位置确定不变。 质量均匀的规则物体的质心在几何中心。 质心与重心不一样,物体尺寸不十分大时,质心 与重心位置重合

例题2-1求腰长为的等腰直角三角形均匀薄板的质心 位置。 解:建立图示坐标,在离原点x处取宽度为dx的面积元, 由于面积元的高度为2y,所以其面积为2ydx=2xdx。 设薄板每单位面积的质量态,则此面积元的质量 dm 2ox dx 三角形质心坐标x是 -a ● 这个结果和熟知的三角形重心位置一致。 让意不贰返可退此
上页 下页 返回 退出 例题2-1 求腰长为a的等腰直角三角形均匀薄板的质心 位置。 这个结果和熟知的三角形重心位置一致。 d c x m x m = 三角形质心坐标xc是 d d m x x = 2 x dx O x y a 解:建立图示坐标, 由于面积元的高度为2y,所以其面积为2ydx=2xdx。 设薄板每单位面积的质量为 ,则此面积元的质量 在离原点x处取宽度为dx的面积元, / 2 2 0 2 2 d 1 2 a x x a = 2 3 = a

例题2-2一段均匀铁丝弯成半圆形,其半径为R,求 此半圆形铁丝的质心。 解:建立如图坐标系。 任取一小段铁丝, d 其长度为dl,质量 d 为dm,以表示铁 R 丝的线密度 dm=λdl x。=0,y。=2/元 y.=lyadl sino.Rd 2元R2 2R2 m m m 元R2 让元不元返司退
上页 下页 返回 退出 例题2-2 一段均匀铁丝弯成半圆形,其半径为R,求 此半圆形铁丝的质心。 任取一小段铁丝, 其长度为dl,质量 为dm,以λ表示铁 丝的线密度 解:建立如图坐标系。 dm = dl 0 , c x = d c y l y m = π 0 R R sin d m = 2 2 R m = 2 2 π R R = 2 / π c y R =

例题2-3确定半径为的均质半球的质心位置。 解:建立如图所示坐标。 已知薄圆盘的质心位于圆心,取 dy 厚度为dy的薄圆盘为质量微元, dm=pdv=pn(R2-y2)dy y=∫dm_ypmR-ydy p2 R3/3 (R2-y)dy 3R 质心在对称轴上 4R3/3 8 距球心3R/8处。 上美子意返可退此
上页 下页 返回 退出 例题2-3 确定半径为R的均质半球的质心位置。 解:建立如图所示坐标。 已知薄圆盘的质心位于圆心,取 厚度为dy的薄圆盘为质量微元, d d m V = R x y O dy m y m yc = d 2 2 0 3 ( ) d 2 / 3 R y R y y R − = π π ( ) 4 / 3 d 3 0 2 2 2 R R y y R − = 8 3R = 质心在对称轴上 距球心3R/8处。 ( ) 2 2 = − π R y y d

三、质心运动定理 设有一个质点系,由个质点组成,它的质心 的位矢: 产= ∑n, ∑m, n+n2+··+nnn n1+m2+··+mn 质心的速度为 d = dr ∑m,dt= >∑m, dt >∑n, >n: 让觉不意返回退成
上页 下页 返回 退出 i i i c m m r r = 设有一个质点系,由 个质点组成,它的质心 的位矢: n n n n m m m m r m r m r + + + + + + = 1 2 1 1 2 2 质心的速度为 t r v c c d d = i i i m t r m = d d i i i m m v = 三、 质心运动定理

质心的加速度为 ∑n, dv, d。= dve dt ∑n,d, dt 2n, 由牛顿第二定律得 ma m d啦=i+F。+++f。 d ma,m d成=方++房++: d m an =mn dg=元++++fm d 让美不意返回退
上页 下页 返回 退出 质心的加速度为 t v a c c d d = i i i m t v m = d d i i i m m a = 由牛顿第二定律得 1 1 1 1 1 12 13 1 d d n v m a m F F F F t = = + + + + 2 2 2 2 2 22 23 2 d d n v m a m F F F F t = = + + + + 2 3 d d n n n n n n n nn v m a m F F F F t = = + + + +