
*§2-8 对称性和守恒定律 问题的提出 宏观 经典力学理论的局限性 低速 守恒定律的普适性 →宏观、微观、低速、高速 守恒定律具有比力学理论更深厚的基础吗? 守恒定律是与宇宙中某些对称性相联系的。 对称性是统治物理规律的规律。 江美不意返回退此
上页 下页 返回 退出 问题的提出 守恒定律是与宇宙中某些对称性相联系的。 对称性是统治物理规律的规律。 守恒定律具有比力学理论更深厚的基础吗? 经典力学理论的局限性 守恒定律的普适性 宏观 低速 宏观、微观、低速、高速 *§2-8 对称性和守恒定律
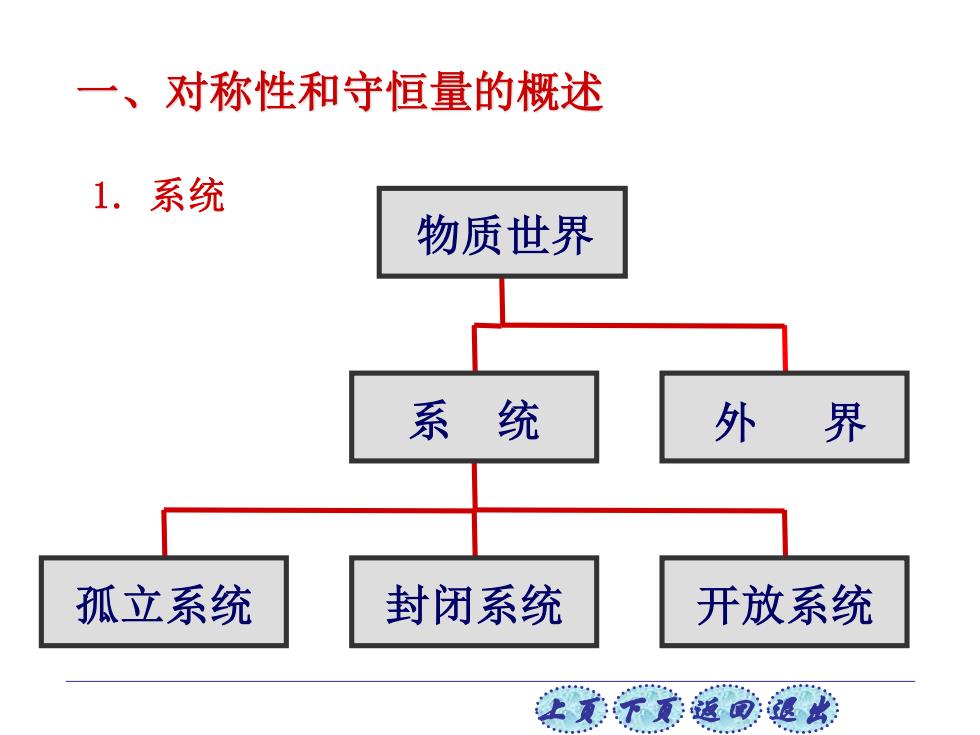
一、对称性和守恒量的概述 1.系统 物质世界 系统 外界 孤立系统 封闭系统 开放系统
上页 下页 返回 退出 一、对称性和守恒量的概述 1. 系统 孤立系统 封闭系统 开放系统 系 统 外 界 物质世界

外力 F-F 内力 元,=-f#一∑f=0 作用在系统上的合力 状态量。 动量、角动量、能量 状态量与系统经历的过程无关。 状态量是系统自身所具有的物理量,与外界无关。 过程量一。冲量、功 过程量与系统自身没有必然的联系。 过程量是由外界对系统过程产生作用的物理量。 让觉下文返面退
上页 下页 返回 退出 状态量 状态量与系统经历的过程无关。 状态量是系统自身所具有的物理量,与外界无关。 过程量 过程量与系统自身没有必然的联系。 过程量是由外界对系统过程产生作用的物理量。 外力 内力 · · · · · · · · i j Fi fi j fj i = = n i F Fi 1 ij ji f f = − 动量、角动量、能量 冲量、功 f = 0 作用在系统上的合力 F F 合 =

2.关于对称性 定义:某一研究对象(体系、事物:物理规律) 对其状态进行某种操作,使其状态由A到B。若 两状态等价(相同),就说该研究对象对该操作 具有对称性。 例 对中心对称 操作 对称性破缺 状态A 状态B 绕中心旋 任意角 状态A与状态B相同或等价 女意套了美返回退晚
上页 下页 返回 退出 2.关于对称性 定义:某一研究对象(体系、事物;物理规律) 对其状态进行某种操作,使其状态由A到B。若 两状态等价(相同),就说该研究对象对该操作 具有对称性。 例 对中心对称 操作 绕中心旋 任意角 状态A 状态B 状态A与状态B相同或等价 • 对称性破缺

3.几种对称操作 A.空间对称操作-空间变换 (1)平移 (2)旋转(3)镜像反射(4)空间反演 B.时间变换 (1)时间平移 (2)时间反演 C.时空联合操作 伽利略变换-力学定律具有不变性 洛伦兹变换-物理定律具有不变性 江美觉返司退
上页 下页 返回 退出 3.几种对称操作 A. 空间对称操作-空间变换 (1)平移 (2)旋转 (3)镜像反射 (4)空间反演 B. 时间变换 (1)时间平移 (2)时间反演 C. 时空联合操作 伽利略变换-力学定律具有不变性 洛伦兹变换-物理定律具有不变性

二、空间平移对称性与动量守恒 空间平移对称性意味着空间的均匀性,表示系统势 函数与位置无关,这将导致动量守恒。 卫+P2=常矢量 讨论一维情况:E,(x)=E,(x+△x) △E,=E(x+△x)-E(x)=0 Epx AE0x aEAx= +4x=0 E 0 Ox Ox, 让意不贰道回:退
上页 下页 返回 退出 空间平移对称性意味着空间的均匀性,表示系统势 函数与位置无关,这将导致动量守恒。 E x E x x p p ( ) = + ( ) 1 2 p p + = 常矢量 ( ) ( ) p P P = + − = E E x x E x 0 p p p p p 1 2 1 2 ( ) 0 E E E E E x x x x x x x = + = + = 讨论一维情况: 二、空间平移对称性与动量守恒
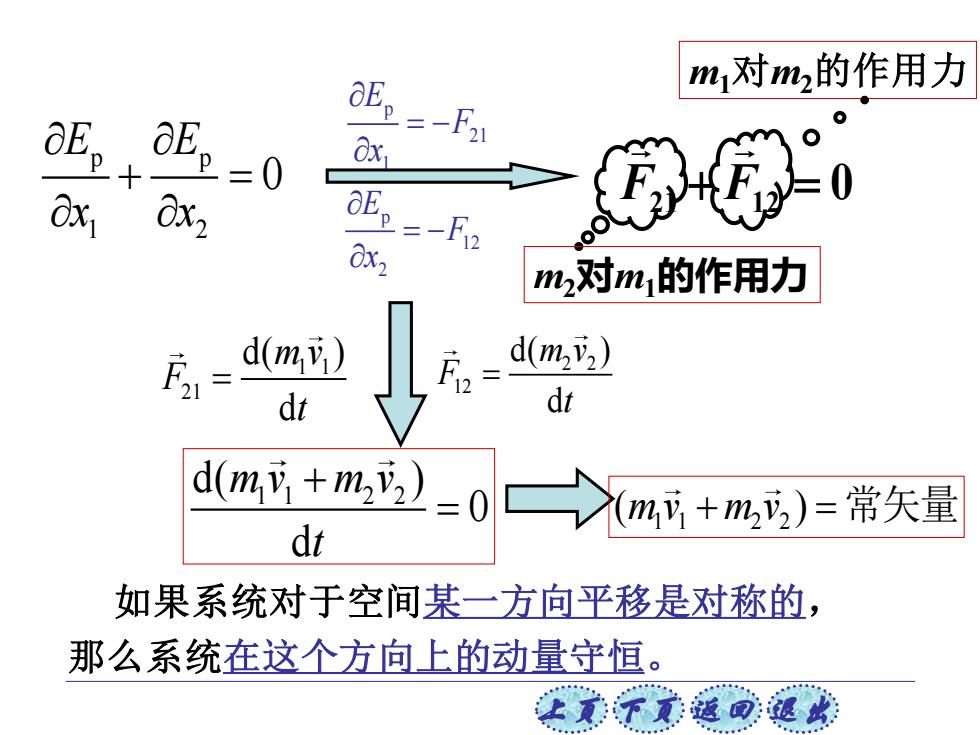
aE-F m1对m2的作用力 0 0x 0x2 0E22-F 0 0x2 m2对m1的作用力 d(m,) d(m22) d(m,+m2) =0>m成+m)=常矢量 dr 如果系统对于空间某一方向平移是对称的, 那么系统在这个方向上的动量守恒。 江美不意返回退此
上页 下页 返回 退出 p p 1 2 0 E E x x + = p 21 1 E F x = − p 12 2 E F x = − 0 F21 + F12 = m2对m1的作用力 m1对m2的作用力 如果系统对于空间某一方向平移是对称的, 那么系统在这个方向上的动量守恒。 1 1 21 d( ) d m v F t = 2 2 12 d( ) d m v F t = 1 1 2 2 d( ) 0 d m v m v t + = 1 1 2 2 ( ) m v m v + = 常矢量

推广:如果系统对于空间任意方向平移是对称的, 那么系统动量守恒。 由力和动量的关系 d啦 F dr ∑万=0→方=∑m西=常矢量 所有速度是对同一个坐标系而言的。 让美不家道可退此
上页 下页 返回 退出 推广: 如果系统对于空间任意方向平移是对称的, 那么系统动量守恒。 Fi = 0 n i i i p m v = = 常矢量 所有速度是对同一个坐标系而言的。 d d p F t 由力和动量的关系 =

三、时间平移对称性与机械能守恒律 时间平移的对称性意味着时间的均匀性,表示系统 的势函数与时间无关,这将导致能量守恒。 讨论一维情况:E,(x,t+△)=E(x,) 对两个粒子的保守系统有: Ep (xt+At)=Ep(x2t) 用泰勒级数展开 E,(x,x,t+△t)=E,(,x2,)+ 正t+高次项 让美觉返司退
上页 下页 返回 退出 时间平移的对称性意味着时间的均匀性,表示系统 的势函数与时间无关,这将导致能量守恒。 讨论一维情况: E x t t E x t p p ( , ( , ) + =) 对两个粒子的保守系统有: ( ) p 1 2 p 1 2 E x x t t E x x t , , ( , , ) + = 用泰勒级数展开 ( ) P p 1 2 p 1 2 , , ( , , ) E E x x t t E x x t t t + = + + 高次项 三、时间平移对称性与机械能守恒律

E,61+)=r,0+要s+高次项 aE,=0 上式中必有: 考虑动能和势能可推导出 dE=0日 E=常数 dt 如果系统对于时间平移是对称的,那么系统 的能量一定守恒一 能量守恒定律 让美不家道可退此
上页 下页 返回 退出 p 0 E t = 上式中必有: 考虑动能和势能可推导出 d 0 d E t = E = 常数 如果系统对于时间平移是对称的,那么系统 的能量一定守恒 ——能量守恒定律 ( ) P p 1 2 p 1 2 , , ( , , ) E E x x t t E x x t t t + = + + 高次项