
§5-1热运动的描述 理想气体模型和状态方程 一、状态参量 1.宏观量—状态参量 平衡态下描述宏观属性的相互独立的物理量。 如压强p、体积V、温度T等。 2.微观量 描述系统内个别微观粒子特征的物理量。如分子 的质量、直径、速度、动量、能量等。 微观量与宏观量有一定的内在联系。 让元子文返回退此
上页 下页 返回 退出 一、状态参量 1. 宏观量——状态参量 平衡态下描述宏观属性的相互独立的物理量。 如压强 p、体积 V、温度 T 等。 2. 微观量 描述系统内个别微观粒子特征的物理量。 如分子 的质量、 直径、速度、动量、能量等。 微观量与宏观量有一定的内在联系。 §5-1 热运动的描述 理想气体模型和状态方程
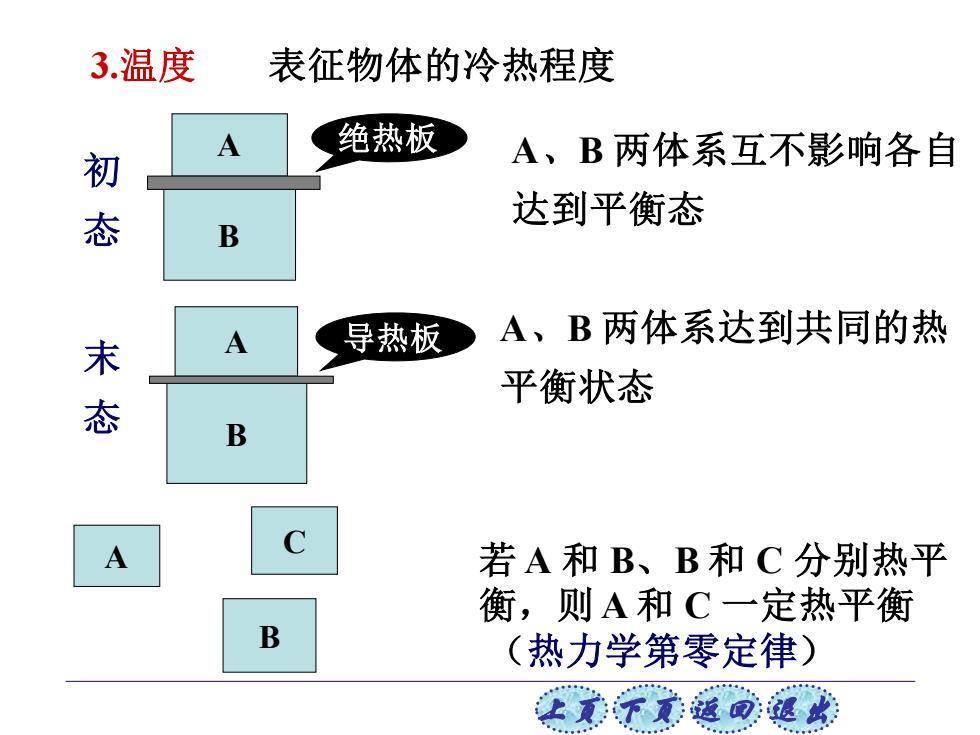
3温度 表征物体的冷热程度 A 绝热板 初 A、B两体系互不影响各自 达到平衡态 B A 导热板 A、B两体系达到共同的热 态 平衡状态 B A 若A和B、B和C分别热平 衡,则A和C一定热平衡 B (热力学第零定律) 上觉子觉道司退欢
上页 下页 返回 退出 3.温度 表征物体的冷热程度 A、B 两体系互不影响各自 达到平衡态 A、B 两体系达到共同的热 平衡状态 A B 绝热板 初 态 A B 导热板 末 态 A B C 若 A 和 B、B 和 C 分别热平 衡,则 A 和 C 一定热平衡 (热力学第零定律)

处在相互热平衡状态的系统拥有某一共同的宏观 物理性质,这个性质称为温度。 温标:温度的数值表示方法。 华氏温标:1714年荷兰华伦海特建立,以水结冰的温 度为32°F,水沸腾的温度为212°F 摄氏温标:1742年瑞典天文学家摄尔修斯建立,以冰 的熔点定为0C,水的沸点定为100°℃ 热力学温标:与工作物质无关的温标,由英国的开尔 文建立,与摄氏温度的数值关系为 T/K=t/°C+273 单位为K(开),称为热力学温度。 元不素道回退埃
上页 下页 返回 退出 处在相互热平衡状态的系统拥有某一共同的宏观 物理性质,这个性质称为温度。 华氏温标:1714年荷兰华伦海特建立,以水结冰的温 度为32°F,水沸腾的温度为212°F 摄氏温标:1742年瑞典天文学家摄尔修斯建立,以冰 的熔点定为0 °C,水的沸点定为100°C 热力学温标:与工作物质无关的温标,由英国的开尔 文建立,与摄氏温度的数值关系为 T t / K / C 273 = + 单位为K(开),称为热力学温度。 温标:温度的数值表示方法

二、平衡态 准静态过程 1热力学系统(热力学研究的对象) 大量微观粒子(分子、原子等)组成的宏观物体。 外界:热力学系统以外的物体。 系统分类(按系统与外界交换特点): 孤立系统:与外界既无能量又无物质交换 封闭系统:与外界只有能量交换而无物质交换 开放系统:与外界既有能量交换又有物质交换 平衡态系统 系统分类(按系统所处状态) 非平衡态系统 让美觉返司退此
上页 下页 返回 退出 二、平衡态 准静态过程 1.热力学系统(热力学研究的对象) 大量微观粒子(分子、原子等)组成的宏观物体。 外界:热力学系统以外的物体。 系统分类(按系统与外界交换特点): 孤立系统:与外界既无能量又无物质交换 封闭系统:与外界只有能量交换而无物质交换 开放系统:与外界既有能量交换又有物质交换 系统分类(按系统所处状态) 平衡态系统 非平衡态系统

2.平衡态 平衡态:在不受外界影响的条件下,系统宏观性质 均匀一致、不随时间变化的状态。 气体状态(p,T)就是指平衡态。 状态1到状态2是一个状态变化的过程。若此 过程足够缓慢,这个过程中每一状态都可近似看作 平衡态。 平衡条件: (1)系统与外界在宏观上无能量和物质的交换, (2)系统的宏观性质不随时间改变。 非平衡态:不具备两个平衡条件之一的系统。 上美子家返可退此
上页 下页 返回 退出 平衡态:在不受外界影响的条件下,系统宏观性质 均匀一致、不随时间变化的状态。 气体状态(p,V,T)就是指平衡态。 状态1到状态2是一个状态变化的过程。若此 过程足够缓慢,这个过程中每一状态都可近似看作 平衡态。 2.平衡态 平衡条件: (1) 系统与外界在宏观上无能量和物质的交换, (2) 系统的宏观性质不随时间改变。 非平衡态: 不具备两个平衡条件之一的系统

说明: ·平衡态是一种热动平衡 处在平衡态的大量分子仍在作热运动,而且因 为碰撞,每个分子的速度经常在变,但是系统的宏 观量不随时间改变。 例如:粒子数 箱子假想分成两相同体积的部分, 达到平衡时,两侧粒子有的穿越 界线,但两侧粒子数相同。 ·平衡态是一种理想状态 让美下元返回:退比
上页 下页 返回 退出 箱子假想分成两相同体积的部分, 达到平衡时,两侧粒子有的穿越 界线,但两侧粒子数相同。 例如:粒子数 说明: · 平衡态是一种理想状态 处在平衡态的大量分子仍在作热运动,而且因 为碰撞, 每个分子的速度经常在变,但是系统的宏 观量不随时间改变。 · 平衡态是一种热动平衡

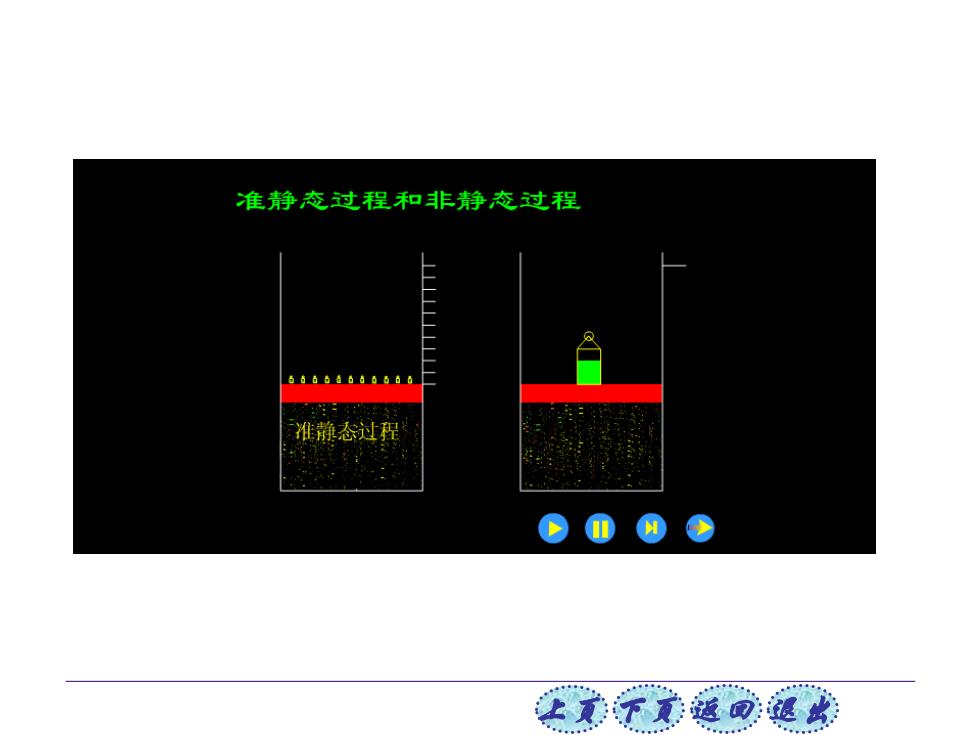
3.准静态过程 当热力学系统在外界影响下,从一个状态到另一 个状态的变化过程,称为热力学过程,简称过程。 准静态过程 热力学过程 非静态过程 准静态过程:系统从一平衡态到另一平衡态,如果过 程中所有中间态都可以近似地看作平衡态的过程。 非静态过程:系统从一平衡态到另一平衡态,过程中 所有中间态为非平衡态的过程。 例:气体 气体 等温 自由 真空 膨胀 膨胀
上页 下页 返回 退出 当热力学系统在外界影响下,从一个状态到另一 个状态的变化过程,称为热力学过程,简称过程。 热力学过程 非静态过程 准静态过程 3.准静态过程 准静态过程:系统从一平衡态到另一平衡态,如果过 程中所有中间态都可以近似地看作平衡态的过程。 非静态过程:系统从一平衡态到另一平衡态,过程中 所有中间态为非平衡态的过程。 气体 自由 膨胀 例: 气体 等温 膨胀 T
准静态过程和非静态过程 准静态过程 让美觉返司退
上页 下页 返回 退出

三、理想气体的状态方程 理想气体的p,V,T满足 p L-C 标准状态: p=1.013×103Pa(或N/m2)→1atm T=273.15K →0°C V%ml=22.4×10-3m3/mol 对质量为m的理想气体 py povopo m m R T To To Mmol 让贰下觉返回退
上页 下页 返回 退出 C pV T 理想气体的 p,V,T 满足 = 标准状态: 3 3 0,mol V 22.4 10 m /mol − = 0 T = 273.15K 5 2 0 p = 1.013 10 Pa ( N/m ) 或 1atm 0 C 对质量为m的理想气体 0 0 0 pV p V T T = 0 0,mol 0 mol p m V T M = mol m R M = 三、理想气体的状态方程

其中R=P% =8.31J/mol.K一普适气体常数 To pr. m RT 理想气体状态方程 M ol 根据状态方程,系统的压 强、体积、温度中任两个量一 I(p,V,T) 定就可确定系统的状态,因此 常用p-V图中的一条曲线来表 (p2,',T) 示系统的准静态过程,曲线上 任一点都表示气体的一个平衡 态,这种图叫状态图。 让美下觉返司速此
上页 下页 返回 退出 0 0,mol 0 p V R T = mol m pV RT M = 其中 = 8.31J/molK——普适气体常数 理想气体状态方程 2 2 2 II( , , ) p V T p O 1 1 1 I( , , ) p V T • • V 根据状态方程,系统的压 强、体积、温度中任两个量一 定就可确定系统的状态,因此 常用p-V 图中的一条曲线来表 示系统的准静态过程,曲线上 任一点都表示气体的一个平衡 态,这种图叫状态图