
§6-2热力学第一定律对于理想气体 准静态过程的应用 一、等体过程气体的摩尔定体热容 等体过程: 系统体积在状态变化过程中始终保持不变。 dy =0 A=0或dA=0 P2 do,dE P Q=E2-E,=△E / 等体过程中,系统对外不作功,吸收的热量 全用于增加内能
上页 下页 返回 退出 系统体积在状态变化过程中始终保持不变。 dV = 0 A A = = 0 d 0 或 QV = E2 − E1 = E dQV = dE 等体过程: 等体过程中,系统对外不作功,吸收的热量 全用于增加内能。 §6-2 热力学第一 定律对于理想气体 准静态过程的应用 一、 等体过程 气体的摩尔定体热容 p O V 1 2 V 2 p 1 p

摩尔定体热容 1mol气体在体积不变时,温度改变1K时所吸收或放 出的热量。 C R dE dT dT 2 即:理想气体的摩尔定体热容是一个只与分子自由 度有关的量。 等体吸热 m Cy(T2-T) 等体内能增量 △E = m Mmol Cv(T,-T),适应于所有过程 让美觉返司退此
上页 下页 返回 退出 等体吸热 即:理想气体的摩尔定体热容是一个只与分子自由 度有关的量。 ,适应于所有过程 1 mol气体在体积不变时,温度改变1K时所吸收或放 出的热量。 d d = d d 2 V V Q E i C R T T = =2 1 mol ( ) V V m Q C T T M = − 2 1 mol ( ) V m E C T T M = − 摩尔定体热容 等体内能增量

二、等压过程气体的摩尔定压热容 等压过程: 系统压强在状态变化过程中始终保持不变。 dp 0 m ΛE= CY(T2-TD 2 A=pdv-p(V;-V) R(T-T) Mmol 上美子意道可退此
上页 下页 返回 退出 等压过程: 系统压强在状态变化过程中始终保持不变。 d 0 p = 2 1 mol ( ) V m E C T T M = − 2 1 2 1 d ( ) V V A p V p V V = = − 2 1 mol ( ) m R T T M = − p O V 1 2 二、 等压过程 气体的摩尔定压热容

=AE+p(V2-V) Op=AE+A= m(Cr+R)(T:-T) M 在等压过程中,理想气体吸热的一部分用于增 加内能,另一部分用于对外作功。 摩尔定压热容: 1mol气体在压力不变时,温度改变1K时所吸收或放 出的热量。 do dE+pdy dE pdv=iR+R dT dT dT dT 2 江美不意返司退此
上页 下页 返回 退出 2 1 mol ( )( ) p V m Q E A C R T T M = + = + − 在等压过程中,理想气体吸热的一部分用于增 加内能,另一部分用于对外作功。 摩尔定压热容: 1 mol气体在压力不变时,温度改变1K时所吸收或放 出的热量。 d d d d d d d d d 2 p Q E p V E p V i C R R T T T T + = = = + = + 2 1 ( ) Q E p V V p = + −
又 Cp=Cr+R 迈耶公式 注意:1mol气体温度改变1K时,在等压过程中比在 等体过程中多吸收8.31J的热量用来对外作功。 Y= i+2>1,叫做热容比 Cp 1 Cy Cp 热容比 单原子分子 3 5 1.67 双原子分子 5 7 1.4 刚性多原子分子 6 8 1.3 上学意滋回退
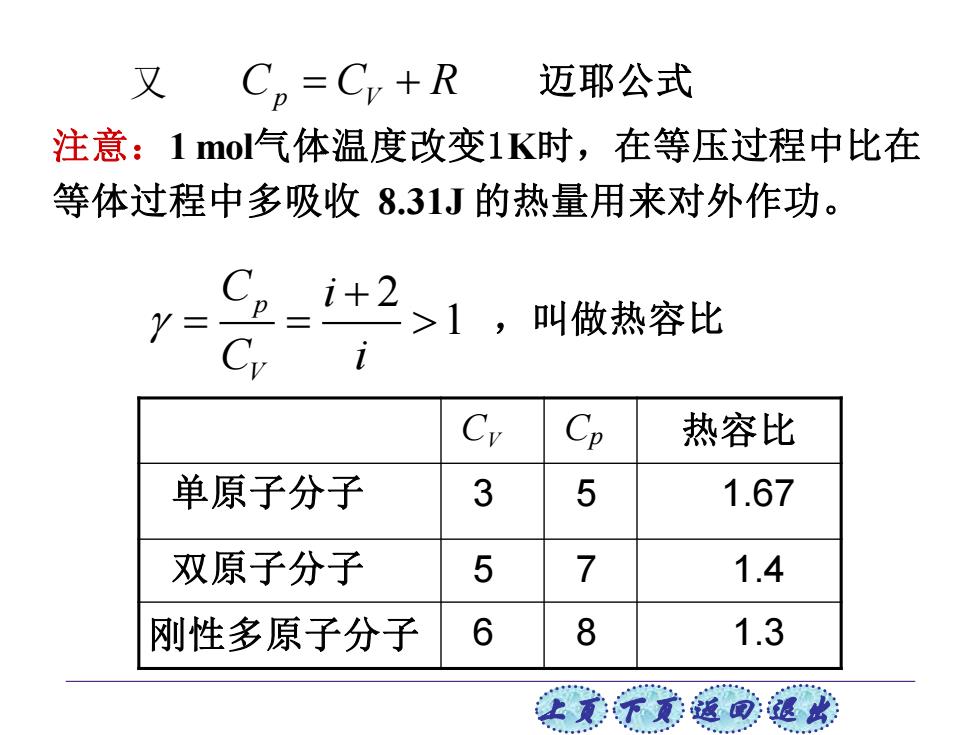
上页 下页 返回 退出 又 迈耶公式 注意:1 mol气体温度改变1K时,在等压过程中比在 等体过程中多吸收 8.31J 的热量用来对外作功。 C C R p V = +2 1 p V C i C i + = = ,叫做热容比 CV Cp 热容比 单原子分子 3 5 1.67 双原子分子 5 7 1.4 刚性多原子分子 6 8 1.3

例题6-1一汽缸中贮有氮气,质量为1.25kg。在标准大气 压下缓慢地加热,使温度升高1K。试求气体膨胀时所作 的功A、气体内能的增量△E以及气体所吸收的热量2。 (活塞的质量以及它与汽缸壁的摩擦均可略去。) 解:因过程是等压的,得 m A= R△T=371J M mol 因=5,所以C=iR/2=20.8J/(moK,可得 △E= CrAT =929J Mmol Q,=E2-E+A=1300J 让美觉返司退
上页 下页 返回 退出 例题6-1 一汽缸中贮有氮气,质量为1.25kg。在标准大气 压下缓慢地加热,使温度升高1K。试求气体膨胀时所作 的功A、气体内能的增量E以及气体所吸收的热量Qp。 (活塞的质量以及它与汽缸壁的摩擦均可略去。) mol 371J m A R T M = = 因i=5,所以CV=iR/2=20.8J/(molK),可得 mol 929J V m E C T M = = 解:因过程是等压的,得 2 1 1300J Q E E A p = − + =

三、等温过程 系统温度在状态变化过程中始终保持不变。 d7 0 △E=0 44前r8 dy 'V V2 m RT In Mmol Mmol P2 在等温过程中,理想气体吸热全部用于对外作功 ,或外界对气体作功全转换为气体放出的热。 让贰不贰通回退
上页 下页 返回 退出 系统温度在状态变化过程中始终保持不变。 dT = 0 E = 0 2 2 1 1 1 mol d d V V T V V m V Q A p V RT M V = = = 2 1 1 1 mol 1 mol 2 ln ln m m V p RT RT M V M p = = 在等温过程中,理想气体吸热全部用于对外作功 ,或外界对气体作功全转换为气体放出的热。 p O V 2 1 三、等温过程

四、绝热过程 系统在状态变化过程中始终与外界没有热交换。 9=0或dQ=0 m A=-(E2-E)= Cy(T2-T) M mol 绝热膨胀过程中,系统对外作的功,是靠内能减 少实现的,故温度降低;绝热压缩过程中,外界对 气体作功全用于增加气体内能,故温度上升。 绝热过程方程: 气体绝热自由膨胀 pV?=C Q=0,A=0,△E=0 TVY-1=C, T-Ypr-=C3 气体 真空 让美觉返司退此
上页 下页 返回 退出 系统在状态变化过程中始终与外界没有热交换。 Q Q = = 0 d 0 或 2 1 2 1 mol ( ) ( ) V m A E E C T T M = − − = − − 绝热膨胀过程中,系统对外作的功,是靠内能减 少实现的,故温度降低;绝热压缩过程中,外界对 气体作功全用于增加气体内能,故温度上升。 C1 pV = 2 1 TV = C − 绝热过程方程: 3 1 T p = C − − 四、绝热过程 气体绝热自由膨胀 气体 真空 Q=0, A=0,E=0

绝热过程方程的推导: 对绝热过程,据热力学第一定律,有 d4 -dE 即 pdy = m CrdT 状态方程 pV= m RT M mol pdv +rdp = m RdT 消去dT得 (Cy+R)pdy=-CrVdp 女美子养适际退此
上页 下页 返回 退出 对绝热过程,据热力学第一定律,有 dA = −dE 即 mol m pV RT M = mol d d d m p V V p R T M + = (CV + R) pdV = −CVVdp mol d dV m p V C T M = − 状态方程 消去dT 得 绝热过程方程的推导:

(Cy+R)pdV=-CrVdp 因为 Cy+R=Cp,Cp/Cr=Y 所以 p 积分得lnp+ylnV=C 即pV'=C 或TW=C, 绝热过程方程 或T-yp=C 让美觉返司退
上页 下页 返回 退出 C R p V C V p V V ( + ) d = − d , / C R C C C V p p V + = = d d 0 p V p V + = 积分得 ln p + lnV = C C1 pV = 即 1 2 1 3 TV C T p C − − − = = 或 或 绝热过程方程 因为 所以