
*§3-6理想流体模型定常流动伯努利方程 一、理想流体模型 流体:液体和气体都具有流动性,统称为流体。 流体特点:流体各部分很容易发生相对运动,因而没 有固定的形状,其形状随容器的形状而异。液体不易 被压缩,具有一定的体积,能形成自由表面;气体易 被压缩,没有固定的体积,不存在自由表面,可弥漫 于整个容器内的空间。 在一些实际问题中,当可压缩性和黏滞性只是 影响运动的次要因素时,可把流体看作绝对不可压 缩,且完全没有黏性的理想流体。 上贰不觉返退此
上页 下页 返回 退出 一、理想流体模型 流体:液体和气体都具有流动性,统称为流体。 流体特点:流体各部分很容易发生相对运动,因而没 有固定的形状,其形状随容器的形状而异。液体不易 被压缩,具有一定的体积,能形成自由表面;气体易 被压缩,没有固定的体积,不存在自由表面,可弥漫 于整个容器内的空间。 在一些实际问题中,当可压缩性和黏滞性只是 影响运动的次要因素时,可把流体看作绝对不可压 缩,且完全没有黏性的理想流体。 *§3-6 理想流体模型 定常流动 伯努利方程

当理想流体流动时,由于忽略了黏性力,所以 流体各部分之间也不存在这种切向力,流动流体仍 然具有静止流体内的压强的特点,即压力总是垂直 于作用面的。 流体动压强:流体在流动时内部的压强称为流体动 压强。 二、定常流动 定常流动:流体流动时,其中任一质元流过不同地 点的流速不尽相同,而且流经同一地点,其流速也 会随时间而变。但在某些常见的情况下,尽管流体 内各处的流速不同,而各处的流速却不随时间而变 化,这种流动称为定常流动。 上文下元道司退此
上页 下页 返回 退出 当理想流体流动时,由于忽略了黏性力,所以 流体各部分之间也不存在这种切向力,流动流体仍 然具有静止流体内的压强的特点,即压力总是垂直 于作用面的。 流体动压强:流体在流动时内部的压强称为流体动 二、定常流动 定常流动:流体流动时,其中任一质元流过不同地 点的流速不尽相同,而且流经同一地点,其流速也 会随时间而变。但在某些常见的情况下,尽管流体 内各处的流速不同,而各处的流速却不随时间而变 化,这种流动称为定常流动。 压强
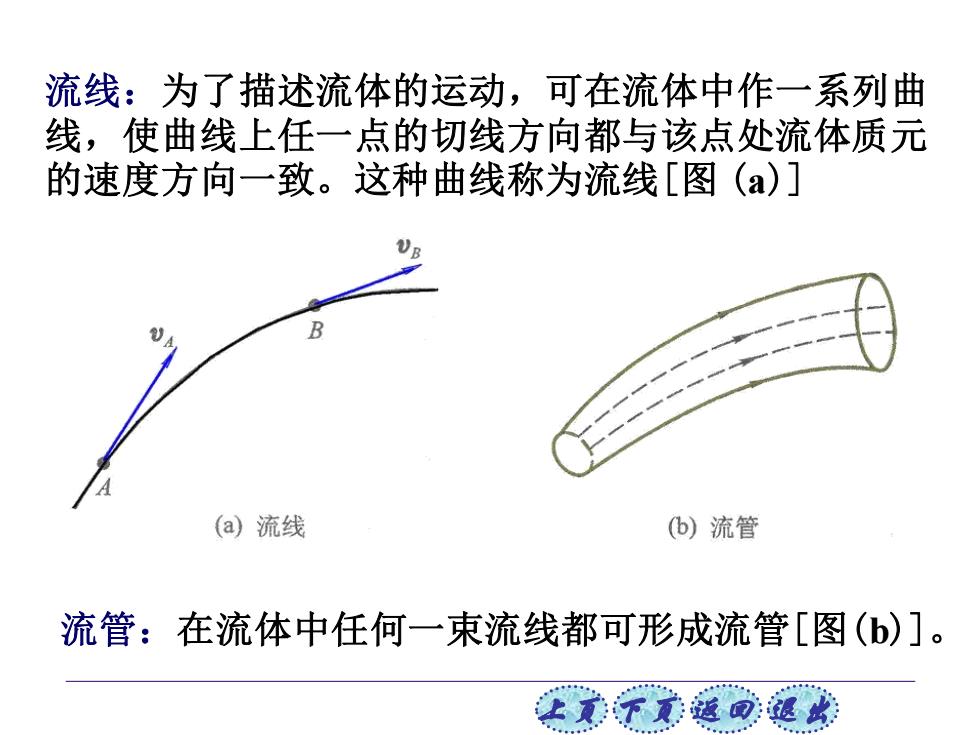
流线:为了描述流体的运动,可在流体中作一系列曲 线,使曲线上任一点的切线方向都与该点处流体质元 的速度方向一致。这种曲线称为流线[图(a)] (a)流线 b)流管 流管:在流体中任何一束流线都可形成流管[图(b)]
上页 下页 返回 退出 流线:为了描述流体的运动,可在流体中作一系列曲 线,使曲线上任一点的切线方向都与该点处流体质元 的速度方向一致。这种曲线称为流线[图 (a)] 流管:在流体中任何一束流线都可形成流管[图(b)]
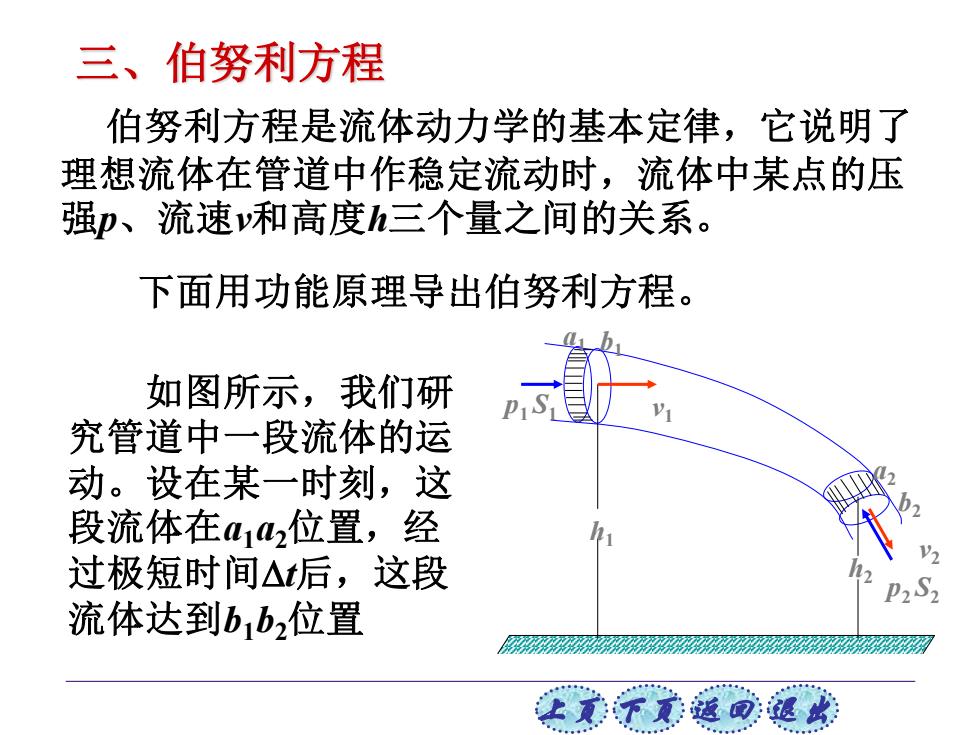
三、伯努利方程 伯努利方程是流体动力学的基本定律,它说明了 理想流体在管道中作稳定流动时,流体中某点的压 强p、流速和高度h三个量之间的关系。 下面用功能原理导出伯努利方程。 如图所示,我们研 究管道中一段流体的运 动。设在某一时刻,这 段流体在4142位置,经 过极短时间△后,这段 P2S2 流体达到b1b2位置 让觉下文道司退
上页 下页 返回 退出 伯努利方程是流体动力学的基本定律,它说明了 理想流体在管道中作稳定流动时,流体中某点的压 强p、流速v和高度h三个量之间的关系。 下面用功能原理导出伯努利方程。 如图所示,我们研 究管道中一段流体的运 动。设在某一时刻,这 段流体在a1a2位置,经 过极短时间t后,这段 流体达到b1b2位置 h2 v1 v2 p2 S2 p1 S1 h1 a1 b1 a2 b2 三、伯努利方程

现在计算在流动过程中,外力对这段流体所作的功。 假设流体没有黏性,管壁对它没有摩擦力,那么,管壁 对这段流体的作用力垂直于它的流动方向,因而不作功。 所以流动过程中,除了重力之外,只有在它前后的流体 对它作功。在它后面的流体推它前进,这个作用力作正 功;在它前面的流体阻碍它前进,这个作用力作负功。 因为时间△极短,所以41b1和2b2是两段极短的位移 在每段极短的位移中,压强、截面积S和流速v都可看 作不变。设p1、S1、y1和p2、S2、2分别是1b1与2b2处 流体的压强、截面积和流速,则后面流体的作用力是 p1S1,位移是y1△t,所作的正功是p11y1△t,而前面流 体作用力作的负功是-p2S22△t,由此,外力的总功是:
上页 下页 返回 退出 现在计算在流动过程中,外力对这段流体所作的功。 假设流体没有黏性,管壁对它没有摩擦力,那么,管壁 对这段流体的作用力垂直于它的流动方向,因而不作功。 所以流动过程中,除了重力之外,只有在它前后的流体 对它作功。在它后面的流体推它前进,这个作用力作正 功;在它前面的流体阻碍它前进,这个作用力作负功。 因为时间t极短,所以a1b1和a2b2是两段极短的位移, 在每段极短的位移中,压强p、截面积S和流速v都可看 作不变。设p1、S1、v1和p2、S2、v2分别是a1b1与a2b2处 流体的压强、截面积和流速,则后面流体的作用力是 p1S1,位移是v1 t,所作的正功是p1S1v1 t,而前面流 体作用力作的负功是-p2S2v2t,由此,外力的总功是:

A=(p,SV-P2S2V)△t 因为流体被认为不可压缩。所以41b1和2b2两小段流体 的体积S1y1△和S2y2△必然相等,用△V表示,则上式可 写成 A=(P-P2)AV 其次,计算这段流体在流动中能量的变化对于稳 定流动来说,在b12间的流体的动能和势能是不改变 的。由此,就能量的变化来说,可以看成是原先在 41b1处的流体,在时间△t内移到了2b2处,由此而引 起的能量增量是 E-E,=(5m2+mgh,)-(号2+mgh) =paI(5+gh)-(5+gh川 让美下觉返司速此
上页 下页 返回 退出 其次,计算这段流体在流动中能量的变化对于稳 定流动来说,在b1a2间的流体的动能和势能是不改变 的。由此,就能量的变化来说,可以看成是原先在 a1b1处的流体,在时间t内移到了a2b2处,由此而引 起的能量增量是 因为流体被认为不可压缩。所以a1b1和a2b2两小段流体 的体积S1v1t和S2v2t必然相等,用V表示,则上式可 写成 A p p V = − ( 1 2 ) 2 1 2 2 2 1 2 1 1 1 ( ) ( ) 2 2 E E mv mgh mv mgh − = + − + A p S V p S V t = − ( 1 1 1 2 2 2 ) 2 2 2 2 1 1 1 1 [( ) ( )] 2 2 = + − + V v gh v gh

从功能原理得 (m,ar=+)(+g】 整理后得 A+号pm时+g4=+2m+P8肠 这就是伯努利方程,它表明在同一管道中任何一点处, 流体每单位体积的动能和势能以及该处压强之和是个 常量。在工程上,上式常写成 +h=常量 pg 2g
上页 下页 返回 退出 )] 2 1 ) ( 2 1 ( ) [( 1 2 2 1 2 p1 − p2 V = V v 2 + gh − v + gh 2 2 1 2 2 1 1 2 2 1 2 1 p + v + gh = p + v + gh 从功能原理得 整理后得 这就是伯努利方程,它表明在同一管道中任何一点处, 流体每单位体积的动能和势能以及该处压强之和是个 常量。在工程上,上式常写成 + + h = 常量 g v g p 2 2

D h三项都相当于长度,分别叫做 pg 压力头、速度头、水头。 所以伯努利方程表明在同一管道的任一处,压 力头、速度头、水头之和是一常量。对作稳定 流动的理想流体,用这个方程对确定流体内部 压力和流速有很大的实际意义,在水利、造船、 航空等工程部门有广泛的应用。 例题3-11水电站常用水库出水管道处水流的动 能来发电。出水管道的直径与管道到水库水面高 度h相比为很小,管道截面积为S。试求出水处水 流的流速和流量。 让美下觉返司速此
上页 下页 返回 退出 、 g p h g v 、 2 2 三项都相当于长度,分别叫做 所以伯努利方程表明在同一管道的任一处,压 力头、速度头、水头之和是一常量。对作稳定 流动的理想流体,用这个方程对确定流体内部 压力和流速有很大的实际意义,在水利、造船、 航空等工程部门有广泛的应用。 压力头、速度头、水头。 例题3-11 水电站常用水库出水管道处水流的动 能来发电。出水管道的直径与管道到水库水面高 度h相比为很小,管道截面积为S。试求出水处水 流的流速和流量

解:把水看作理想流体。在水库中出水管道很小, 水流作定常流动。如图所示,在出水管中取一条流 线b。在水面和管口这两点处的流速分别为y和yb。 在大水库小管道的情况下,水面的流速远比管口 的小,可以忽略不计, 即v=0。取管口处高度 为0,则水面高度为h。 在a、b两点的压强都是 大气压p。Pb=p0。由伯 努利方程,得 2P+D,=Pgh+p。 上下返回退此
上页 下页 返回 退出 2 0 0 1 2 b v p gh p + = + 解:把水看作理想流体。在水库中出水管道很小, 水流作定常流动。如图所示,在出水管中取一条流 线ab。在水面和管口这两点处的流速分别为va和vb。 在大水库小管道的情况下,水面的流速va远比管口 的小,可以忽略不计, 即va=0。取管口处高度 为0,则水面高度为h。 在a、b两点的压强都是 大气压pa =pb=p0。由伯 努利方程,得
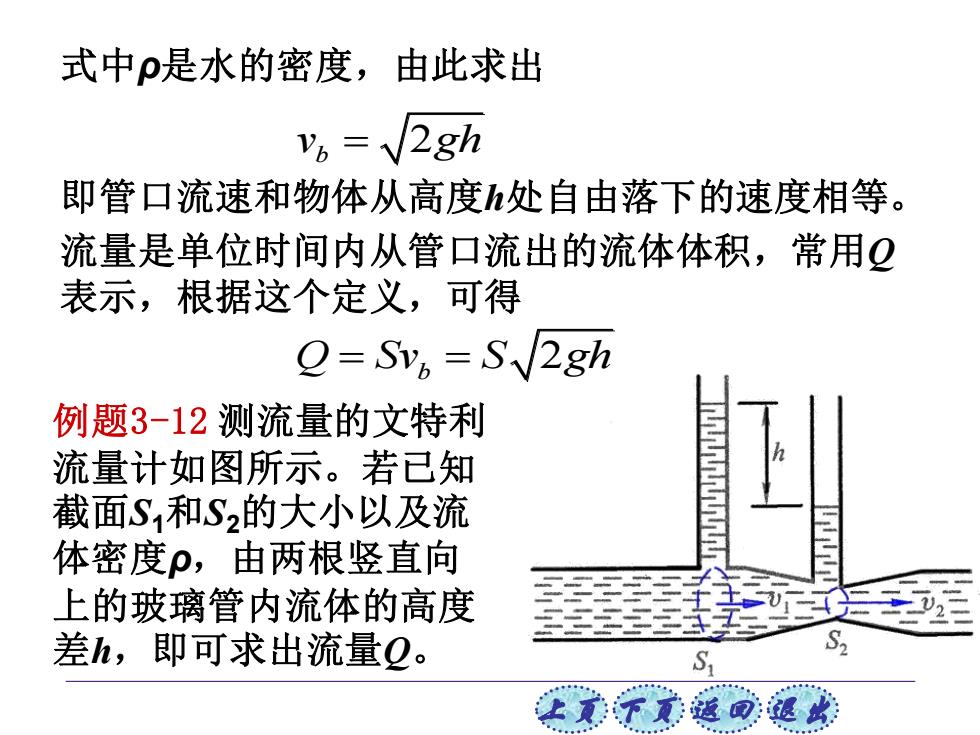
式中p是水的密度,由此求出 y6=√2gh 即管口流速和物体从高度h处自由落下的速度相等。 流量是单位时间内从管口流出的流体体积,常用Q 表示,根据这个定义,可得 O=Sv,=S 2gh 例题3-12测流量的文特利 流量计如图所示。若已知 截面S和S2的大小以及流 体密度ρ,由两根竖直向 上的玻璃管内流体的高度 差h,即可求出流量Q。 S2 S
上页 下页 返回 退出 式中ρ是水的密度,由此求出 v gh b = 2 即管口流速和物体从高度h处自由落下的速度相等。 流量是单位时间内从管口流出的流体体积,常用Q 表示,根据这个定义,可得 Q Sv S gh = =b 2 例题3-12 测流量的文特利 流量计如图所示。若已知 截面S1和S2的大小以及流 体密度ρ,由两根竖直向 上的玻璃管内流体的高度 差h,即可求出流量Q