
§4-2 相对论速度变换 考虑一质点P在空间的运动,从K和K'系 来看,速度分别是 u=(hux,uy,lu:) h=(lu',t'y,l) 根据速度的定义: x dy dz u:= t' dt dt u.- dx' d dz' dr' dr' dr' 让意下文滋回退欢
上页 下页 返回 退出 考虑一质点 P 在空间的运动,从 K 和 K′系 来看,速度分别是 (u u u ) (u u u ) u x y z u = x y z = , , , , 根据速度的定义: d d d , , d d d d d d , , d d d x y z x y z x y z t t t x y z t t t u u u u u u = = = = = = §4-2 相对论速度变换

由洛伦兹坐标变换 dx'= (dx-vdi) V1-B2 w-r dx-vdt u.-y 上面两式之比 .= d dx 1-
上页 下页 返回 退出 由洛伦兹坐标变换 2 1 d (d d ) 1 x x v t = − − 2 2 1 d d d 1 v t t x c = − − 上面两式之比 ' 2 2 d d d d 1 x x x x v t u v u v v t x u c c − − = = − −

同样得可导出 4V1-B2 1-4 u:1-B2 1- 24 让美觉返司退
上页 下页 返回 退出 2 ' 2 1 1 y y x u u v u c − = − 同样得可导出 2 ' 2 1 1 z z x u u v u c − = −

洛伦兹速度变换式 正变换 逆变换 ux-v ux-v I、 ux 24x 1、 V -Ux 1-B2 uy 1) 2 1 4,V1-B2 1. u.v1-B2 u, 2 u 让贰了京适可:退此
上页 下页 返回 退出 洛伦兹速度变换式 正变换 逆变换 ' 2 2 ' 2 2 ' 2 1 1 1 1 1 x x x y y x z z x u v u v u c u u v u c u u v u c − = − − = − − = − ' ' 2 ' 2 ' 2 ' 2 ' 2 1 1 1 1 1 x x x y y x z z x u v u v u c u u v u c u u v u c − = − − = − − = −
说明 a.在v<c的情况,上式即变为伽利略速度变换式。 b.在洛伦兹速度变换下,光速不变。 例题4-2在地面上测到有两个飞船A、B分别以 +0.9c和一0.9c的速度沿相反的方向飞行,如图所示。 求飞船A相对于飞船B的速度有多大。 0.09c 0.09c
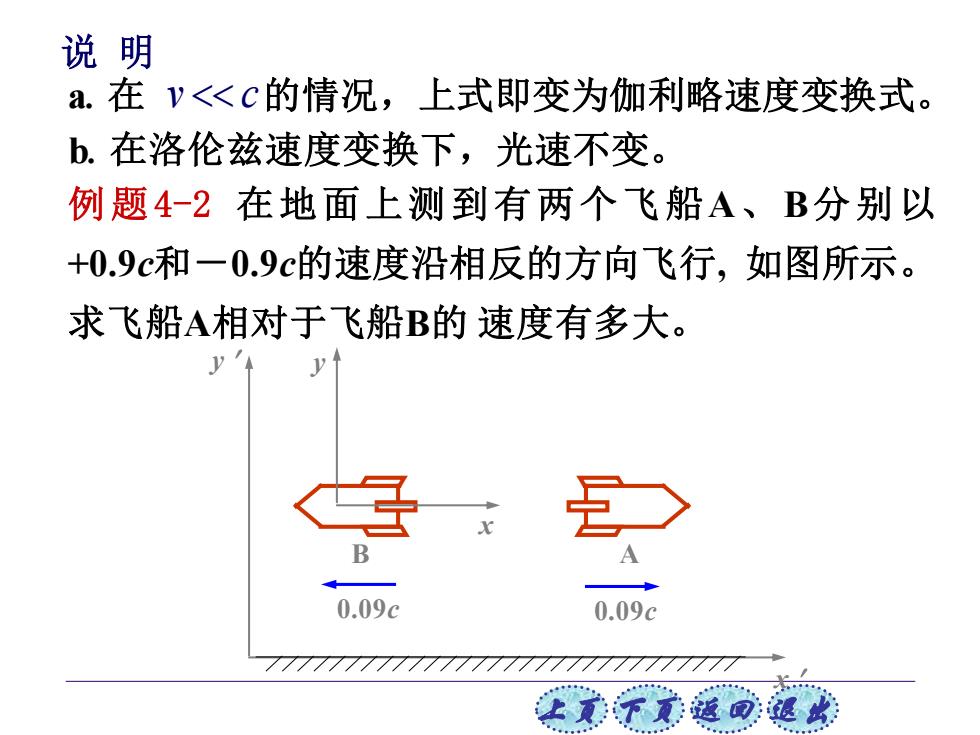
上页 下页 返回 退出 说 明 b. 在洛伦兹速度变换下,光速不变。 a. 在 v c 的情况,上式即变为伽利略速度变换式。 例题4-2 在地面上测到有两个飞船A、B分别以 +0.9c和-0.9c的速度沿相反的方向飞行, 如图所示。 求飞船A相对于飞船B的 速度有多大。 y y x x B A 0.09c 0.09c

解:设K系被固定在飞船B上,则飞船B在其中为静止, 而地面对此参考系以y=0.9c的速度运动。以地面为参考 系K',则飞船A相对于K'系的速度按题意为=0.9c, 可求得飞船A对K系的速度,亦即相对于飞船B的速度: +v u, =0.994c Yu. 1+ 如用伽利略速度变换进行计算,结果为 u,=u,+v=1.8c>c 两者大相径庭。相对论给出山x<c。一般地说,按相 对论速度变换,在和都小于c的情况下,不可能 大于c
上页 下页 返回 退出 2 0.994 1 x x x u v u c vu c + = = + 1.8 x x u u v c c = + = 如用伽利略速度变换进行计算,结果为 解: 设K系被固定在飞船B上,则飞船B在其中为静止, 而地面对此参考系以v=0.9c 的速度运动。以地面为参考 系 ,则飞船A相对于 系的速度按题意为 , 可求得飞船A对K系的速度,亦即相对于飞船B的速度: K K 0.9 x u c = 两者大相径庭。相对论给出ux<c。一般地说,按相 对论速度变换,在v和 都小于c的情况下,u不可能 大于c。 u

选择进入下一节 §4-0教学基本要求 §4-1狭义相对论基本原理 洛伦滋变换 §4-2相对论速度变换 §43狭义相对论的时空观 §4-4狭义相对论动力学基础 *§4-5广义相对论简介 让美觉返司退
上页 下页 返回 退出 选择进入下一节 §4-0 教学基本要求 §4-1 狭义相对论基本原理 洛伦兹变换 §4-2 相对论速度变换 §4-3 狭义相对论的时空观 §4-4 狭义相对论动力学基础 *§4-5 广义相对论简介