
§6-6 熵 玻耳兹曼关系 一、熵 大量的生产实践表明: 当给定系统处于非平衡态时,总要发生从非平衡 态向平衡态的自发性过渡; 当给定系统处于平衡态时,系统却不可能发生从 平衡态向非平衡态的自发性过渡。 为解决实际过程的方向问题,引入描述平衡态的 状态函数一熵,据它的单向变化的性质可判断实 际过程的方向。 可逆热机的效率 7=9+9-T-g 2 L 让意子元返回:退埃
上页 下页 返回 退出 大量的生产实践表明: 当给定系统处于非平衡态时,总要发生从非平衡 态向平衡态的自发性过渡; 当给定系统处于平衡态时,系统却不可能发生从 平衡态向非平衡态的自发性过渡。 为解决实际过程的方向问题,引入描述平衡态的 状态函数——熵,据它的单向变化的性质可判断实 际过程的方向。 可逆热机的效率 2 1 2 1 1 2 T T T Q Q Q − = + = §6-6 熵 玻耳兹曼关系 一、 熵
规定:吸热为正,放热为负。22为负值,得到 2或 + =0 T T 结论:系统经历一可逆卡诺循环后,热温比总和为零。 有限个卡诺循环组成的可逆循环 可逆循环bedefghija由几个 等温和绝热过程组成。从图可看 出,它相当于有限个卡诺循环( abja,bcghb,defgd)组成的。 所以有 =0 让美下元返回:退欢
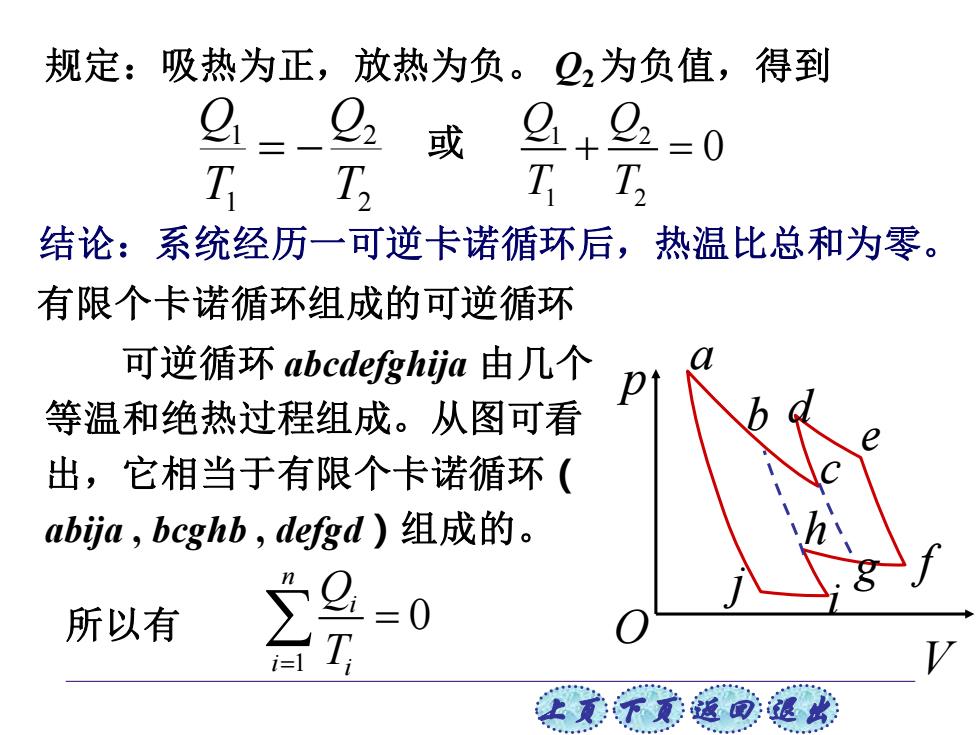
上页 下页 返回 退出 规定:吸热为正,放热为负。 Q2 为负值,得到 结论:系统经历一可逆卡诺循环后,热温比总和为零。 2 2 1 1 T Q T Q = − 1 2 1 2 0 Q Q T T + = 有限个卡诺循环组成的可逆循环 j i f h g e d c b a p V O 可逆循环 abcdefghija 由几个 等温和绝热过程组成。从图可看 出,它相当于有限个卡诺循环( abija , bcghb , defgd)组成的。 1 0 n i i i Q = T 所以有 = 或
无限个卡诺循环组成的 可逆循环 变为: =0 可逆 ∮表示积分沿整个循环过程进行,d2表示在各无 限小过程中吸收的微小热量。 任一可逆循环,用一系列微小可逆卡诺循环代替。 即:对任一可逆循环,其热温比之和为零。 女贰子意通返回退此
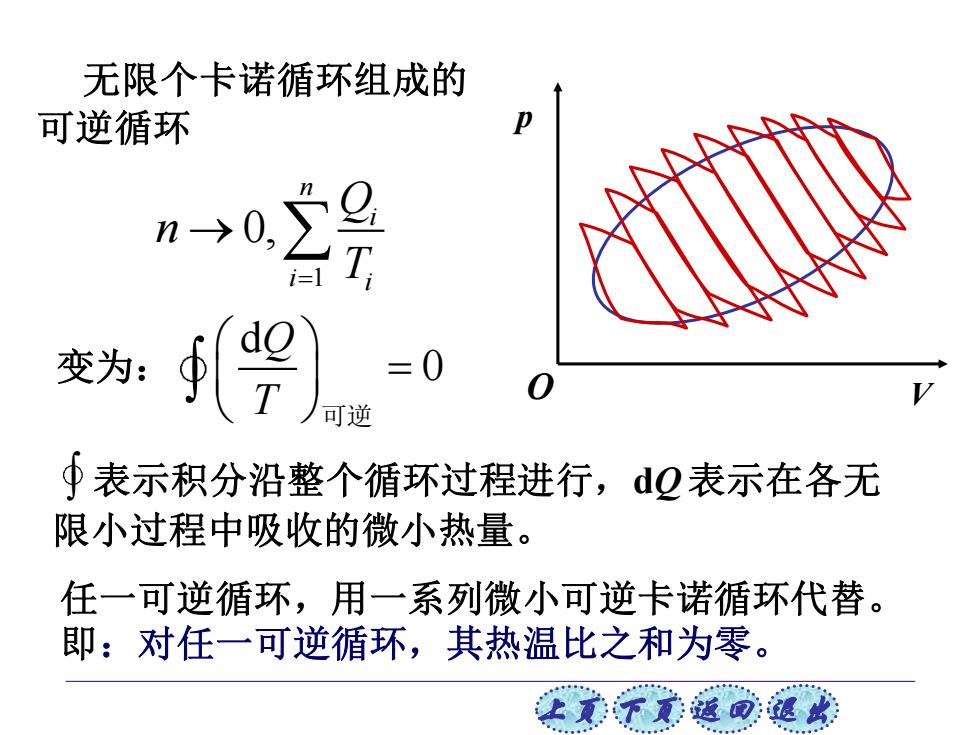
上页 下页 返回 退出 任一可逆循环,用一系列微小可逆卡诺循环代替。 即:对任一可逆循环,其热温比之和为零。 无限个卡诺循环组成的 可逆循环 p O V 1 0, n i i i Q n = T → 变为: d 0 Q T = 可逆 表示积分沿整个循环过程进行,dQ 表示在各无 限小过程中吸收的微小热量。

状态图上任意两点1和2间,连两条路径a和b, 成为一个可逆循环。 2(S2) +r1d=0 1(S) 9-9 积分 ∫d幽值与1、2之间经历的过程无关, 只由始末两个状态有关。 定义:系统从初态变化到末态时,其熵的增量等于初 态和末态之间任意一可逆过程热温比的积分 0 王文不美菠面:退收
上页 下页 返回 退出 1( ) S1 2( ) a S2 b 状态图上任意两点 1 和 2间,连两条路径 a 和 b, 成为一个可逆循环。 2 1 1 2 d d 0 Q Q a b T T + = 2 2 1 1 d d Q Q a b T T = 积分 的值与1、2之间经历的过程无关, 只由始末两个状态有关。 2 1 dQ T 定义:系统从初态变化到末态时,其熵的增量等于初 态和末态之间任意一可逆过程热温比的积分

对有限小过程 5-8=f 可逆 对无限小过程 dS- d 说明: 可逆 熵是系统状态的函数; 两个确定状态的熵变是一确定的值,与过程无关。 熵的计算 (1)如果系统经历的过程不可逆,那么可以在始末 状态之间设想某一可逆过程,以设想的过程为积分路 径求出熵变 dS ss=9 可逆 可逆
上页 下页 返回 退出 说明: 熵是系统状态的函数; 两个确定状态的熵变是一确定的值,与过程无关。 2 2 1 1 dQ S S T − = 可逆 Q S T = 可逆 d d 对有限小过程 对无限小过程 (1)如果系统经历的过程不可逆,那么可以在始末 状态之间设想某一可逆过程,以设想的过程为积分路 径求出熵变: 熵的计算 2 2 1 1 dQ S S T − = 可逆 d d , Q S T = 可逆

(2)如果系统由几部分组成,各部分熵变之和等于 系统总的熵变: AS=∑AS i=1 二、自由膨胀的不可逆性 系统从状态1(V1,p1,T1S1),经自由膨胀(d2-0)到状 态2(V,P2,T2S2),其中T=T2,VP2,计 算此不可逆过程的熵变。 设计一可逆等温膨胀过程从1到2,吸热dQ>0 S,-s-9-小-世2 RIn Mmol 气体在自由膨胀过程中,它的熵是增加的。 江觉子觉道司退此
上页 下页 返回 退出 (2)如果系统由几部分组成,各部分熵变之和等于 系统总的熵变: = = N i i S S 1 系统从状态1(V1 , p1 ,T1 ,S1),经自由膨胀(dQ=0)到状 态2(V2 , p2 ,T2 ,S2),其中T1= T2,V1 p2 ,计 算此不可逆过程的熵变。 设计一可逆等温膨胀过程从 1到2,吸热dQ>0 − = 2 2 1 1 d T Q S S 2 1 2 1 mol d d V V p V m V R T M V = = 2 mol 1 ln 0 m V R M V = 气体在自由膨胀过程中,它的熵是增加的。 二、 自由膨胀的不可逆性
系统的这种不可逆性可用气体动理论来解释。 A室充满气体,B室为真空; 当抽去中间隔板后,分子自由 A 膨胀,待稳定后,分子据A、 Co B室分类,分子处于两室的几 a 率相等,四个分子在容器中分 布共有16种。 分子的分布 bcd acd abd abc a b ab ac ad bc bd abcd 0 A d cd B 0 计 abcd a 6 d bcd acd abd cd bd bc ad ac abc ab 态 1 1 4 4 6 16
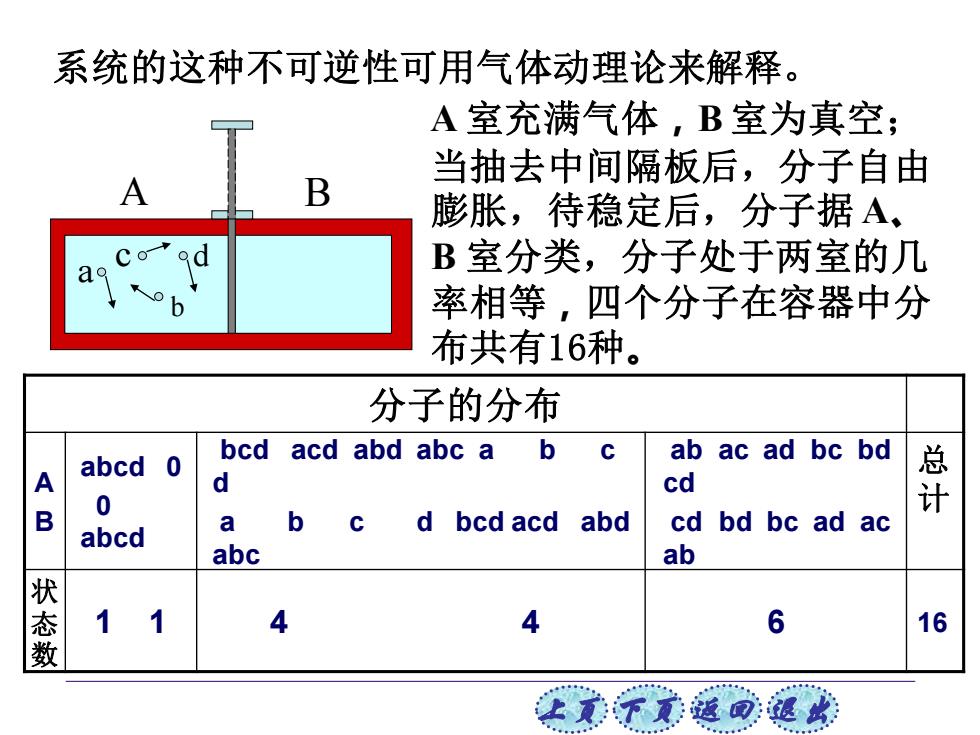
上页 下页 返回 退出 系统的这种不可逆性可用气体动理论来解释。 A 室充满气体,B 室为真空; 当抽去中间隔板后,分子自由 膨胀,待稳定后,分子据 A、 B 室分类,分子处于两室的几 率相等,四个分子在容器中分 布共有16种。 A B a b c d 分子的分布 A B abcd 0 0 abcd bcd acd abd abc a b c d a b c d bcd acd abd abc ab ac ad bc bd cd cd bd bc ad ac ab 总 计 状 态 数 1 1 4 4 6 16

宏观状态 AB 微观状态 微观态数目2 宏观状态概率 4 0 abed 1 1=1 24-16 abc d bed a 3 4 44 abd cda b 2=16 ab cd be ad ac bd bd ac 6 ad bc cd ab 9 bed abd 44 3 4 2=16 acd acb 4 abcd 24-16 上文不美返回退以
上页 下页 返回 退出 A B 4 4 0 2 2 1 4 宏观状态 微观状态 abcd ab cd ac bd ad bc 0 4 微观态数目 6 1 宏观状态概率 bc ad bd ac cd ab 3 1 abc d abd c bcd a cda b 3 1 a bcd b acd abcd c abd d acb 4 1 1 2 16 = 4 4 4 2 16 = 4 6 6 2 16 = 4 4 4 2 16 = 4 1 1 2 16 =

上述各微观状态出现的几率相等,系统处于分布微 观状态数最多的宏观状态的几率最大。 对于N个分子的系统与此类似。如1mol气体分 子系统,所有分子全退回A室的概率为 1 26x1023 →0 故气体自由膨胀是不可逆的。 它实质上反映了系统内部发生的过程总是由概率小 的宏观状态向概率大的宏观状态进行;即由包含微观 状态数少的宏观状态向包含微观状态数多的宏观状态 进行。 与之相反的过程没有外界影响,不可能自动进行。 让元子文返回退此
上页 下页 返回 退出 上述各微观状态出现的几率相等,系统处于分布微 观状态数最多的宏观状态的几率最大。 故气体自由膨胀是不可逆的。 它实质上反映了系统内部发生的过程总是由概率小 的宏观状态向概率大的宏观状态进行;即由包含微观 状态数少的宏观状态向包含微观状态数多的宏观状态 进行。 与之相反的过程没有外界影响,不可能自动进行。 对于 N 个分子的系统与此类似。如 1 mol 气体分 子系统,所有分子全退回 A 室的概率为 0 2 1 23 610 →

三、玻耳兹曼关系 用W表示系统所包含的微观状态数,或理解为宏观状 态出现的概率,叫热力学概率或系统的状态概率。 考虑到在不可逆过程中,有两个量是在同时增加,一 个是状态概率W,一个是熵。 玻耳兹曼从理论上证明其关系如下: S=kInW 上式称为玻耳兹曼关系,k为玻耳兹曼常数。 熵的这个定义表示它是分子热运动无序性或混乱性 的量度。系统某一状态的熵值越大,它所对应的宏观 状态越无序。 让美下元返回退欢
上页 下页 返回 退出 用W 表示系统所包含的微观状态数,或理解为宏观状 态出现的概率,叫热力学概率或系统的状态概率。 考虑到在不可逆过程中,有两个量是在同时增加,一 个是状态概率W,一个是熵。 玻耳兹曼从理论上证明其关系如下: 上式称为玻耳兹曼关系,k 为玻耳兹曼常数。 熵的这个定义表示它是分子热运动无序性或混乱性 的量度。系统某一状态的熵值越大,它所对应的宏观 状态越无序。 S k W = ln 三、 玻耳兹曼关系