§7-4静电场的环路定理电势 一、静电场力作功 点电荷电场中试验电 荷qo从P1点经任意路 径到达P2点。 在路径上任一点附近 取元位移dl dl cos dr 点电荷电场力的功: 0 dA=goE.dl =go E cos Odl 让美下觉返同速
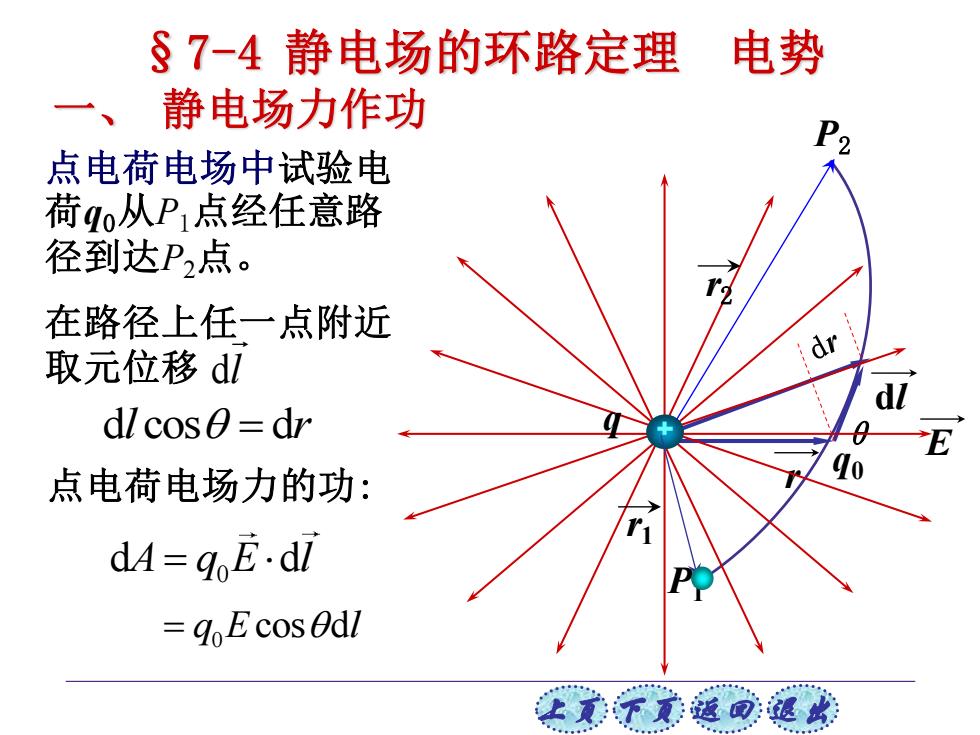
上页 下页 返回 退出 P1 P2 q0 θ dl E r q r1 r2 §7-4 静电场的环路定理 电势 一、 静电场力作功 点电荷电场中试验电 荷q0从P1点经任意路 径到达P2点。 在路径上任一点附近 取元位移 l d 点电荷电场力的功: 0 d d A q E l = 0 = q E l cos d dl cos = dr

X 9192 dr 4元80 qo由P1到P2电场力做功 小×g山 -2 992(1-1 4元80 作功与路径无关 r 点电荷系的电场中 根据电场的叠加性,试探电荷受多个电场作用 E=E,+E++E
上页 下页 返回 退出 q0由 P1到 P2电场力做功 ) 1 1 ( 4π 0 2 1 1 2 r r q q = − − 作功与路径无关 点电荷系的电场中 根据电场的叠加性,试探电荷受多个电场作用 E E E En = 1 + 2 + + r r q q d 4π 1 2 1 2 0 = A = dA = 2 1 d 4π 1 2 1 2 0 r r r r q q

电场力对试验电荷o做功为 A-9E.dj b =g心兵d+g心Ed++Edi =A+A+.+A 总功也与路径无关。 结论:试验电荷在任意给定的静电场中移动时,电 场力对qo做的功仅与试探电荷的电量及路径的起点 和终点位置有关,而与具体路径无关。 静电场是保守场,静电场力是保守力。 让美下觉返面退此
上页 下页 返回 退出 试验电荷在任意给定的静电场中移动时,电 场力对q0做的功仅与试探电荷的电量及路径的起点 和终点位置有关,而与具体路径无关。 电场力对试验电荷q0做功为 A q E l b a = 0 d 0 1 0 2 0 d d d b b b n a a a = + + + q E l q E l q E l = + + + A A A 1 2 n 总功也与路径无关。 = = − n i i P i P r r qq 1 0 0 1 2 1 1 4π 结论: 静电场是保守场,静电场力是保守力
二、静电场的环路定理 试验电荷g在静电场中沿任意闭合路径L运动一周 时,电场力对q作的功A=? 安培 上贰不觉返回退此
上页 下页 返回 退出 二、 静电场的环路定理 试验电荷q0在静电场中沿任意闭合路径L运动一周 时,电场力对q0作的功A=? 安培

在闭合路径L上任取两点P1、P2,将L分成L1、L2两段, A-fF-di=gofE.d (L1) (L2) =gEd-%E.dl月 (L) (L2 L 即A=gofE.d7=0 让美觉返司退
上页 下页 返回 退出 在闭合路径L上任取两点P1、P2,将L分成L1、 L2两段, P2 P1 L2 L1 = = A F l L d = + q E l P P d 2 1 0 (L1) (L2) = − q E l P P d 2 1 0 (L1) (L2) = 0 d = 0 A q E l L 即 q E l L 0 d q E l P P d 1 2 0 q E l P P d 2 1 0

静电场的环路定理 在静电场中,场强沿任意闭合路径的线积分 (称为场强的环流)恒为零。 fE.d7-0 该定理还可表达为:电场强度的环流等于零。 任何力场,只要其场强的环流为零,该力场就叫 保守力场或势场。 综合静电场高斯定律和环路定理,可知静电场 是有源的保守力场,又由于电场线是不闭合的,即 不形成旋涡的,所以静电场是无旋场。 上贰不觉返退
上页 下页 返回 退出 静电场的环路定理 d = 0 E l L 在静电场中,场强沿任意闭合路径的线积分 (称为场强的环流)恒为零。 该定理还可表达为:电场强度的环流等于零。 任何力场,只要其场强的环流为零,该力场就叫 保守力场或势场。 综合静电场高斯定律和环路定理,可知静电场 是有源的保守力场,又由于电场线是不闭合的,即 不形成旋涡的,所以静电场是无旋场

三、电势 电势能 由环路定理知,静电场是保守场。 保守场必有相应的势能,对静电场则为电势能。 静电力的功,等于静电势能的减少。 Aw=go∫E.di=-AE=Wg-g 选N为静电势能的零点,用“0”表示,则 wv=g心E.d 让美下觉返司速此
上页 下页 返回 退出 静电力的功,等于静电势能的减少。 三、 电势 由环路定理知,静电场是保守场。 保守场必有相应的势能,对静电场则为电势能。 选N为静电势能的零点,用“0”表示,则 0 d N MN M A q E l = E W W M N = − = − 0 0 d M M W q E l = 电势能

电势 某点电势能WM与o之比只取决于电场,定义为 该点的电势。单位:V(伏特) 90 电势零点的选取是任意的。对有限带电体一般以 无限远或地球为零点。 由上式可以看出,静电场中某点的电势在数值上等 于单位正电荷放在该点处时的电能,也等于单位正 电荷从该点经任意路径到电势零点处无穷远处)时电 场力所作的功
上页 下页 返回 退出 某点电势能WM与q0之比只取决于电场,定义为 该点的电势。 电势 电势零点的选取是任意的。对有限带电体一般以 无限远或地球为零点。 0 M M W V q = 0 d M = E l 单位: V (伏特) 由上式可以看出,静电场中某点的电势在数值上等 于单位正电荷放在该点处时的电能,也等于单位正 电荷从该点经任意路径到电势零点处(无穷远处)时电 场力所作的功

电势差 电场中两点电势之差(电压) Uw=w-Vx=∫yE.dl 上式表明,静电场中两点M、N的电势差,等于单 位正电荷在电场中从M经任意路径到达N点时电场 力所作的功。 AM =9o(VM-Vx) 上式是计算电场力作功和计算 电势能变化常用公式。 1eV=1.60×10-19J 沿着电场线方向,电势降低。 让美下觉返同速
上页 下页 返回 退出 电势差 电场中两点电势之差(电压) 沿着电场线方向,电势降低。 U V V MN M N = − M N d N M = E l 上式表明,静电场中两点M、N的电势差,等于单 位正电荷在电场中从M经任意路径到达N点时电场 力所作的功。 0 ( ) A q V V MN M N = − 上式是计算电场力作功和计算 电势能变化常用公式。 1eV=1.60×10-19J
四、电势的计算 点电荷的电势 点电荷的电场它= 1_qe, 4π8r2 r-小g 积分得 可见,点电荷周围空间任一点 的电势与该点距离点电荷的 4元E0r 距离r成反比。 正、负点电荷周围电势分布特点
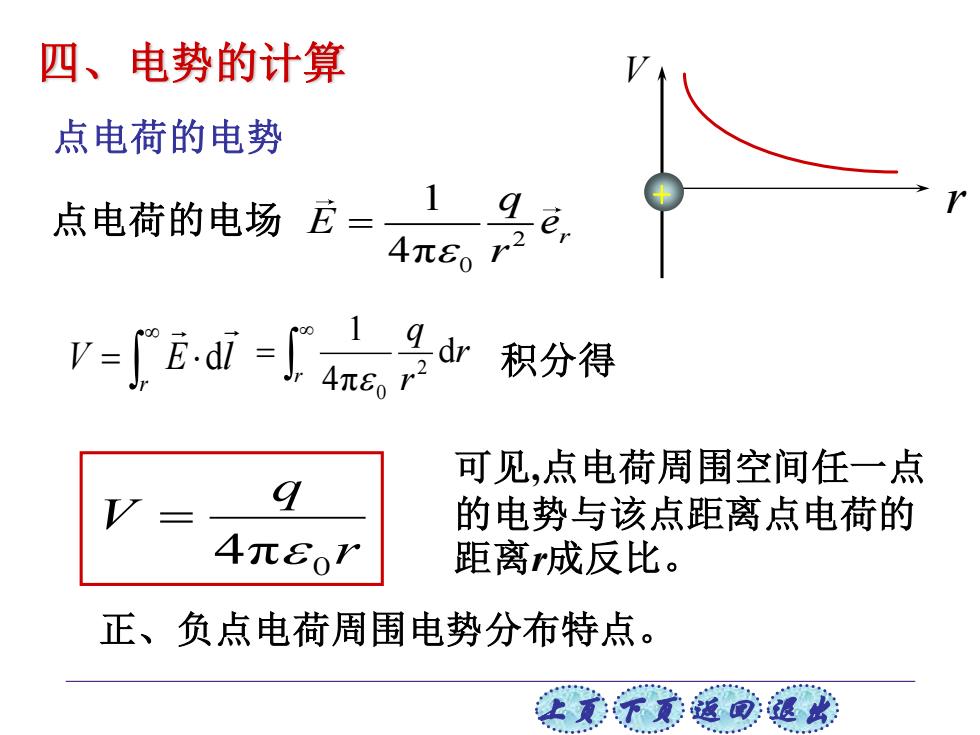
上页 下页 返回 退出 四、电势的计算 点电荷的电势 点电荷的电场 V + r 2 0 1 4π r q E e r = V E l r = d r q V 4π 0 = r r q r d 4π 1 2 0 = 积分得 可见,点电荷周围空间任一点 的电势与该点距离点电荷的 距离r成反比。 正、负点电荷周围电势分布特点