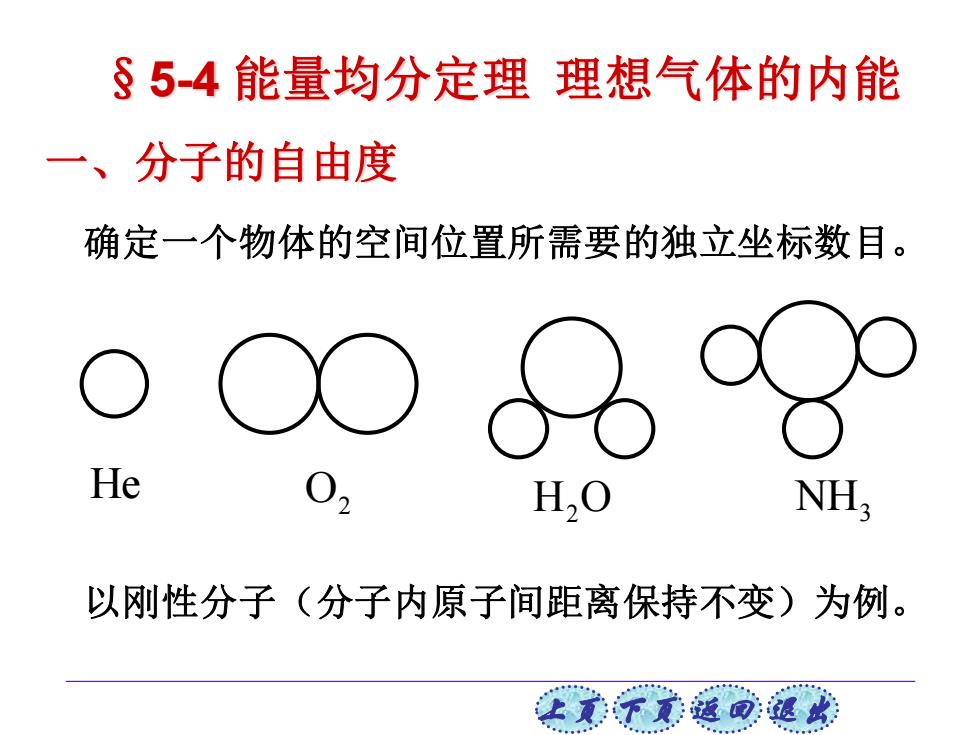
§5-4能量均分定理理想气体的内能 一、分子的自由度 确定一个物体的空间位置所需要的独立坐标数目。 He H.C NH; 以刚性分子(分子内原子间距离保持不变)为例。 让美觉返司退
上页 下页 返回 退出 一、分子的自由度 确定一个物体的空间位置所需要的独立坐标数目。 以刚性分子(分子内原子间距离保持不变)为例。 He O2 H O2 NH3 §5-4 能量均分定理 理想气体的内能
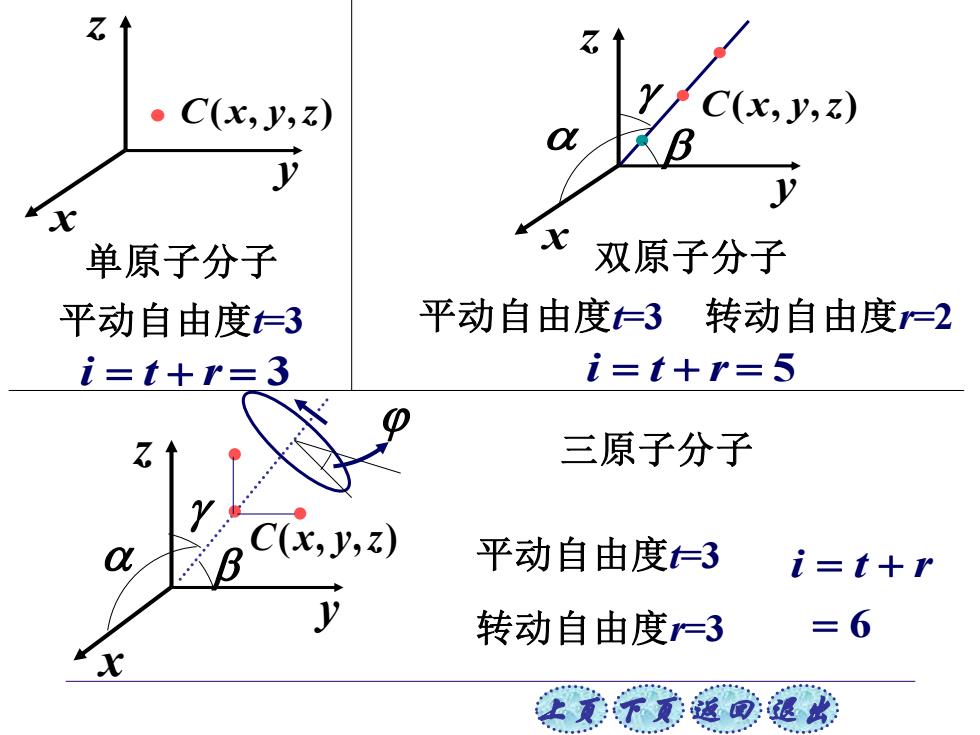
乙 ·C(x,y,) 单原子分子 双原子分子 平动自由度3 平动自由度3转动自由度=2 i=t+r=3 i=t+r=5 三原子分子 C(x,y,z) 平动自由度3 i=t+r 转动自由度=3 =6 上美不意通可退此
上页 下页 返回 退出 z x y C(x, y,z) 双原子分子 x z y C(x, y,z) 单原子分子 平动自由度t=3 i = t + r = 3 平动自由度t=3 转动自由度r=2 i = t + r = 5 C(x, y,z) x z y 三原子分子 平动自由度t=3 转动自由度r=3 = 6 i = t + r

二、能量均分定理 -1m-3kr =v =1 2 1 121 -m mv=m 2 =k 2 气体分子沿x以z三个方向运动的平均平动动能完全 相等,可以认为分子的平均平动动能3kT2均匀分配 在每个平动自由度上。 能均分定理:平衡态下,不论何种运动,相应于每 一个可能自由度的平均动能都是kT2。 如果气体分子有个自由度,则分子的平均动能为kT2. 王觉下元菠面:退收
上页 下页 返回 退出 二、能量均分定理 2 k 1 3 2 2 = = mv kT 2 2 2 2 3 1 v v v v x = y = z = mvx mvy mvz kT 2 1 2 1 2 1 2 1 2 2 2 = = = 气体分子沿 x,y,z 三个方向运动的平均平动动能完全 相等,可以认为分子的平均平动动能3kT/2均匀分配 在每个平动自由度上。 能均分定理:平衡态下,不论何种运动,相应于每 一个可能自由度的平均动能都是kT/2。 如果气体分子有i个自由度,则分子的平均动能为ikT/2

三、理想气体的内能 分子间相互作用 →分子间相互作用的势能=0 可以忽略不计 理想气体的内能=所有分子的热运动动能之总和 1mo理想气体的内能为E,=N,(兮K)=)R7 一定质量理想气体的内能为E= m i RT 温度改变,内能改变量为△E=
上页 下页 返回 退出 三、理想气体的内能 分子间相互作用 可以忽略不计 分子间相互作用的势能=0 理想气体的内能=所有分子的热运动动能之总和 1mol理想气体的内能为 0 0 ( ) 2 2 i i E N kT RT = = 一定质量理想气体的内能为 mol 2 m i E RT M = 温度改变,内能改变量为 mol 2 m i E R T M =

选择进入下一节 §5-0教学基本要求 §5-1热运动的描述理想气体模型和物态方程 §5-2分子热运动和统计规律 §5-3理想气体的压强和温度公式 §5-4能量均分定理理想气体的内能 §55麦克斯韦速率分布律 *§5-6麦克斯韦-玻耳兹曼能量分布律重力场中粒 子按高度的分布 §5-7分子碰撞和平均自由程 *§5-8气体的输运现象 *§5-9真实气体范德瓦尔斯方程 上觉子觉道司退欢
上页 下页 返回 退出 选择进入下一节 §5-0 教学基本要求 §5-1 热运动的描述 理想气体模型和物态方程 §5-2 分子热运动和统计规律 §5-3 理想气体的压强和温度公式 §5-4 能量均分定理 理想气体的内能 §5-5 麦克斯韦速率分布律 *§5-6 麦克斯韦-玻耳兹曼能量分布律 重力场中粒 子按高度的分布 §5-7 分子碰撞和平均自由程 *§5-8 气体的输运现象 *§5-9 真实气体 范德瓦尔斯方程