
*§3-7牛顿力学的内在随机性混沌 一、线性科学和非线性科学 1.线性科学 牛顿建立的经典力学属于线性科学范畴。所谓 线性是指量与量之间成正比关系,用直角坐标形象 地画出来,是一条直线。 在线性系统中,部分之和等于整体,描述线性系 统的方程遵从叠加原理,即方程的不同解相加仍然 是个解。 2.非线性科学 非线性则指整体不等于部分之和,叠加原理失效。 非线性方程两个解之和不再是方程的解。 让贰不觉返回退此
上页 下页 返回 退出 一、线性科学和非线性科学 牛顿建立的经典力学属于线性科学范畴。所谓 线性是指量与量之间成正比关系,用直角坐标形象 地画出来,是一条直线。 在线性系统中,部分之和等于整体,描述线性系 统的方程遵从叠加原理,即方程的不同解相加仍然 是个解。 非线性则指整体不等于部分之和,叠加原理失效。 非线性方程两个解之和不再是方程的解。 1.线性科学 2. 非线性科学 *§3-7 牛顿力学的内在随机性 混沌

3.线性和非线性物理现象的区分 第一,线性现象一般表现为时空中的平滑运动, 并可用性能良好的函数表示;而非线性现象则表现为 从规则运动向不规则运动的转化和跃变。 第二,线性系统往往表现为对外界的影响成比例 地变化;而非线性系统中参量在一些关节点上的极微 小变化,可引起系统运动形式的决定性改变。 第三,反映在连续介质中的波动上,线性行为表 现为色散引起波包的弥散,导致结构的消失,而非线 性作用却可促使空间规整性结构的形成和维持。 自然界大量存在的相互作用是非线性的,线性作 用只不过是非线性作用在一定条件下的近似。 王觉下元菠面:退收
上页 下页 返回 退出 3. 线性和非线性物理现象的区分 第一,线性现象一般表现为时空中的平滑运动, 并可用性能良好的函数表示;而非线性现象则表现为 从规则运动向不规则运动的转化和跃变。 第二,线性系统往往表现为对外界的影响成比例 地变化;而非线性系统中参量在一些关节点上的极微 小变化,可引起系统运动形式的决定性改变。 第三,反映在连续介质中的波动上,线性行为表 现为色散引起波包的弥散,导致结构的消失,而非线 性作用却可促使空间规整性结构的形成和维持。 自然界大量存在的相互作用是非线性的,线性作 用只不过是非线性作用在一定条件下的近似

二、混沌和牛顿力学的内在随机性 1.混沌 由确定性方程描述的简单系统可以出现极为复 杂的貌似随机的无规运动,这就是混沌。 常见的混沌现象 ()天体力学中的地球上流星的起源问题 太阳系的小行星大部分存在于火星与木星之间, 因此地球上的流星也只能起源于这个小行星带。但 是这个小行星带离地球很远,只有偏心率达到57% 的小行星的轨道才能与地球轨道相交
上页 下页 返回 退出 二、混沌和牛顿力学的内在随机性 由确定性方程描述的简单系统可以出现极为复 杂的貌似随机的无规运动,这就是混沌。 1.混沌 常见的混沌现象 (1)天体力学中的地球上流星的起源问题 太阳系的小行星大部分存在于火星与木星之间, 因此地球上的 流星也只能起源于这个小行星带。但 是这个小行星带离地球很远,只有偏心率达到57% 的小行星的轨道才能与地球轨道相交

考虑非共面效应和木星轨道平面相对于行星带的缓慢 变化,发现混沌运动确实可以使偏心率达到60%。 Wisdom通过具体计算,能够给出与观察一致的流 星轨道与丰度,特别是所谓的“下午效应”(即下 午观察到的流星是上午的两倍)。 (2)地磁场的混沌运动 地球的磁场不断地改换极性,而且每种极性维 持的时间间隔是无规则的,这可能是由于地球内部 物质与电荷的经向与纬向的两种运动耦合产生的。 两个方向的运动及两个方向磁场的相互作用会产生 混沌运动。 让美下觉返司速此
上页 下页 返回 退出 考虑非共面效应和木星轨道平面相对于行星带的缓慢 变化,发现混沌运动确实可以使偏心率达到60%。 Wisdom通过具体计算,能够给出与观察一致的流 星轨道与丰度,特别是所谓的“下午效应”(即下 午观察到的流星是上午的两倍)。 (2)地磁场的混沌运动 地球的磁场不断地改换极性,而且每种极性维 持的时间间隔是无规则的,这可能是由于地球内部 物质与电荷的经向与纬向的两种运动耦合产生的。 两个方向的运动及两个方向磁场的相互作用会产生 混沌运动

3)生理学中的“反”混沌-动态病 传统生理学认为,健康人的心率是规则的,具 有周期性。然而更为精确的测量与研究发现,心律 节奏与时间的变化是极不规则的,即心率在时间上 是混沌的。 并不指混乱不堪无规可循,而是确定性系统的内 在随机性的表现,是一种无周期的有序。 动态病-以异常时间组织结构为特征的疾病 动态病的出现不在于人体中的“混沌”,而恰恰在 于出现了“周期性”。 -“反混沌
上页 下页 返回 退出 (3)生理学中的“反”混沌-动态病 传统生理学认为,健康人的心率是规则的,具 有周期性。然而更为精确的测量与研究发现,心律 节奏与时间的变化是极不规则的,即心率在时间上 是混沌的。 并不指混乱不堪无规可循,而是确定性系统的内 在随机性的表现,是一种无周期的有序。 动态病-以异常时间组织结构为特征的疾病 动态病的出现不在于人体中的“混沌”,而恰恰在 于出现了“周期性”。 -“反混沌

正常个体身上各个主要系统中的各种节律之间 有着错综复杂的相互关系,这些节律极少表现出绝 对的周期性。 体内功能的混沌标志着健康, 而周期性行为却可能预示着疾病。 沁张正是由于混沌系统可在范围十分广泛的各种 条件下工作,它们具有高度的适应性和灵活性, 可使系统应付多变环境中出现的种种突变。 长若系统表现为周期运动,那么系统就只有很 少的运动模式,无法应付多变的环境中所出现的 种种突变,这会导致系统损伤和功能失调。 王文不美菠面:退收
上页 下页 返回 退出 正常个体身上各个主要系统中的各种节律之间 有着错综复杂的相互关系,这些节律极少表现出绝 对的周期性。 结论 体内功能的混沌标志着健康, 而周期性行为却可能预示着疾病。 正是由于混沌系统可在范围十分广泛的各种 条件下工作,它们具有高度的适应性和灵活性, 可使系统应付多变环境中出现的种种突变。 若系统表现为周期运动,那么系统就只有很 少的运动模式,无法应付多变的环境中所出现的 种种突变,这会导致系统损伤和功能失调

2.内随机性 随机性:在一定条件下,如果系统的某个状态 既可能出现,也可能不出现。 外随机性 系统自身不会出现随机性,随机性来 自系统外部或某些尚不清楚的原因的 干扰作用。 内随机性 看来完全确定的系统(用确定的微 分方程描述)内部产生的随机性。 混沌现象产生的根源在系统自身,而不在外部的影响。 上美子家返可这此
上页 下页 返回 退出 2.内随机性 随机性:在一定条件下,如果系统的某个状态 既可能出现,也可能不出现。 系统自身不会出现随机性,随机性来 自系统外部或某些尚不清楚的原因的 干扰作用。 外随机性 内随机性 看来完全确定的系统(用确定的微 分方程描述)内部产生的随机性。 混沌现象产生的根源在系统自身,而不在外部的影响

我们把混沌说成是在确定性动力学系统中出 现的一种貌似随机的运动。“确定性”是指描述动 力学系统的微分方程中的系数都是确定的,没有概 率性因素。对确定的初始值,确定性方程应给出确 定的解,描述着系统确定的行为。但在某些非线性 系统中,这种过程会因初始值极微小的扰动而产生 很大变化。由于系统的这种初值敏感性,从物理上 看,这过程似乎是随机的,但这种随机性是确定性 系统内部所固有的,所以被叫做内存随机性。具有 内在随机性的动力学系统,通常兼有规则运动和随 机运动的两种不同区域。随着某种参数变化,随机 区域可能逐渐扩大,甚至吞掉规则运动的区域。 让美下文返面退
上页 下页 返回 退出 我们把混沌说成是在确定性动力学系统中出 现的一种貌似随机的运动。“确定性”是指描述动 力学系统的微分方程中的系数都是确定的,没有概 率性因素。对确定的初始值,确定性方程应给出确 定的解,描述着系统确定的行为。但在某些非线性 系统中,这种过程会因初始值极微小的扰动而产生 很大变化。由于系统的这种初值敏感性,从物理上 看,这过程似乎是随机的,但这种随机性是确定性 系统内部所固有的,所以被叫做内存随机性。具有 内在随机性的动力学系统,通常兼有规则运动和随 机运动的两种不同区域。随着某种参数变化,随机 区域可能逐渐扩大,甚至吞掉规则运动的区域
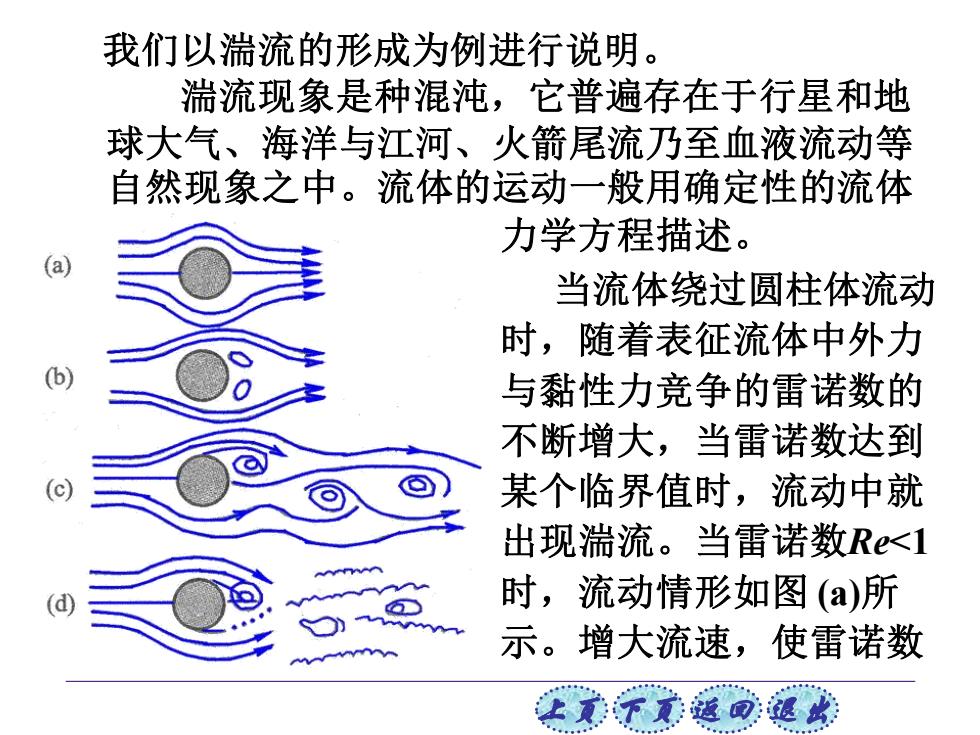
我们以湍流的形成为例进行说明。 湍流现象是种混沌,它普遍存在于行星和地 球大气、海洋与江河、火箭尾流乃至血液流动等 自然现象之中。流体的运动一般用确定性的流体 力学方程描述。 当流体绕过圆柱体流动 时,随着表征流体中外力 与黏性力竞争的雷诺数的 不断增大,当雷诺数达到 某个临界值时,流动中就 出现湍流。当雷诺数Re<1 d 时,流动情形如图(a)所 示。增大流速,使雷诺数
上页 下页 返回 退出 我们以湍流的形成为例进行说明。 湍流现象是种混沌,它普遍存在于行星和地 球大气、海洋与江河、火箭尾流乃至血液流动等 自然现象之中。流体的运动一般用确定性的流体 当流体绕过圆柱体流动 时,随着表征流体中外力 与黏性力竞争的雷诺数的 不断增大,当雷诺数达到 某个临界值时,流动中就 出现湍流。当雷诺数Re<1 时,流动情形如图 (a)所 示。增大流速,使雷诺数 力学方程描述

R20时,可看到圆柱体后面出现两个对称的 涡旋,如图(b)所示。当雷诺数达到40左右, 又发生另一次突变:一个涡旋被拉长后摆脱 柱体,漂向下游;柱后另一侧的流体转了一 个弯,形成新的涡旋。这些涡旋交替产生、 脱落,向下游移去,如图(心)所示。当雷诺数 R104,出现图(d所示的另一次转变湍流形 成了。由边界层里产生的小涡旋中充满着一 条条细带,其流动是紊乱无规的,这就是湍 流状态。在流体力学中就这么一个没有单位 让美下元返藏退
上页 下页 返回 退出 Re≈20时,可看到圆柱体后面出现两个对称的 涡旋,如图(b)所示。当雷诺数达到40左右, 又发生另一次突变:一个涡旋被拉长后摆脱 柱体,漂向下游;柱后另一侧的流体转了一 个弯,形成新的涡旋。这些涡旋交替产生、 脱落,向下游移去,如图(c)所示。当雷诺数 Re≈104,出现图(d)所示的另一次转变湍流形 成了。 由边界层里产生的小涡旋中充满着一 条条细带,其流动是紊乱无规的,这就是湍 流状态。在流体力学中就这么一个没有单位