
电兹感应匀题 13-1 13-2 13-3 13-4 13-5 13-6 13-7 13-8 13-9 13-1013-11 13-1213-13 13-14 13-15 13-13 13-1713-1813-1913-2013-2113-22 13-2313-24 13-2513-2613-2713-2813-2913-3013-3113-32 13-3313-3413-3513-3613-3713-3813-3913-40 结束 习题总目录
电磁感应习题 13-9 13-10 13-11 13-12 13-13 13-14 13-15 13-13 13-17 13-18 13-19 13-20 13-21 13-22 13-23 13-24 13-25 13-26 13-27 13-28 13-29 13-30 13-31 13-32 13-33 13-34 13-35 13-36 13-37 13-38 13-39 13-40 13-1 13-2 13-3 13-4 13-5 13-6 13-7 13-8 结束 习题总目录
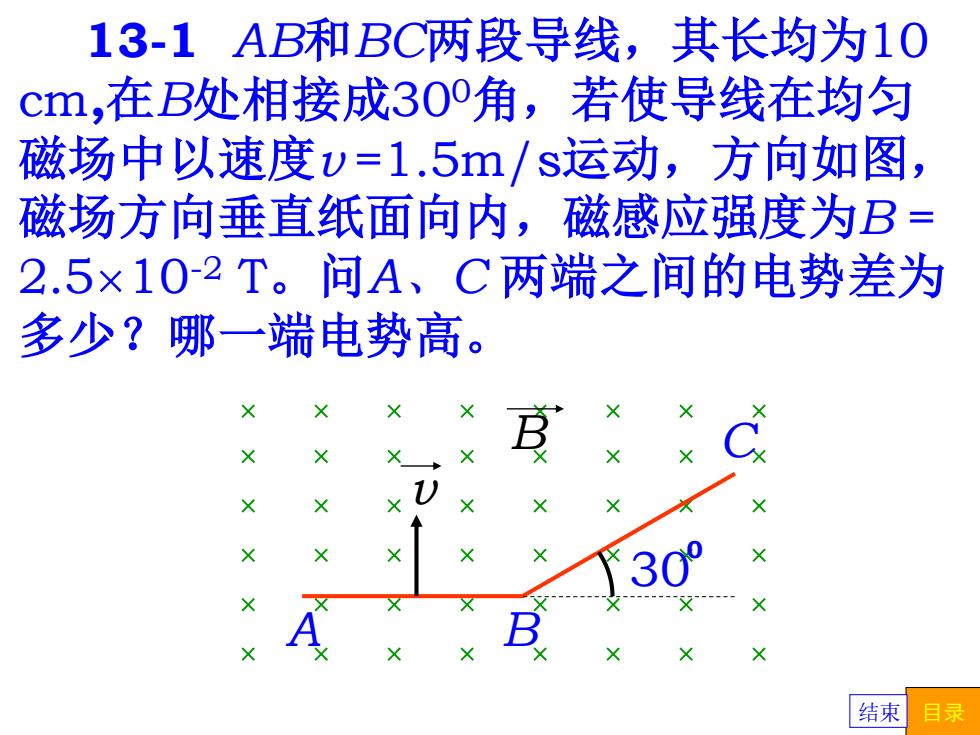
13-1AB和BC两段导线,其长均为10 cm,在B处相接成300角,若使导线在均匀 磁场中以速度v=1.5m/s运动,方向如图, 磁场方向垂直纸面向内,磁感应强度为B= 2.5×102T。问A、C两端之间的电势差为 多少?哪一端电势高。 结束 目录
13-1 AB和BC两段导线,其长均为10 cm,在B处相接成300角,若使导线在均匀 磁场中以速度v =1.5m/s运动,方向如图, 磁场方向垂直纸面向内,磁感应强度为B = 2.5×10-2 T。问A、C 两端之间的电势差为 多少?哪一端电势高。 × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × × 30 A B C v 0 B 结束 目录

己知:1=10cm,v=1.5m/s,B=2.5×10-2T 求:UAC 解:& =Blv(1+cos30) =B11+S)】 =1.5×2.5×102x10x10-21+号) =7.0×10-3(V0 UA>U 结束目录
B v 1 300 e = l ( +cos ) 已知: l =10cm, v =1.5m/s, B =2.5×10-2 T 求:UAC 解: 2 3 = Bl v(1+ ) UA >UC =1.5×2.5×10-2×10×10-2 2 3 (1+ ) = 7.0×10-3 (V) 结束 目录

13-2一均匀磁场与矩形导体回路面法线 单位矢量en间的夹角为0-π/3(如图), 已知磁感应强度B随时间线形增加,即B=kt (>O),回路的AB边长为1,以速度v向右运动, 设t=O时,AB边在x=0处,求:任意时刻回 路中感应电动势的大小和方向。 结束 目录
13-2 一均匀磁场与矩形导体回路面法线 单位矢量en间的夹角为θ=π/3(如图), 已知磁感应强度B 随时间线形增加,即B =kt (k>0),回路的AB边长为 l,以速度v 向右运动, 设t = 0时,AB边在x =0处,求:任意时刻回 路中感应电动势的大小和方向。 q A B x n v e B 结束 目录
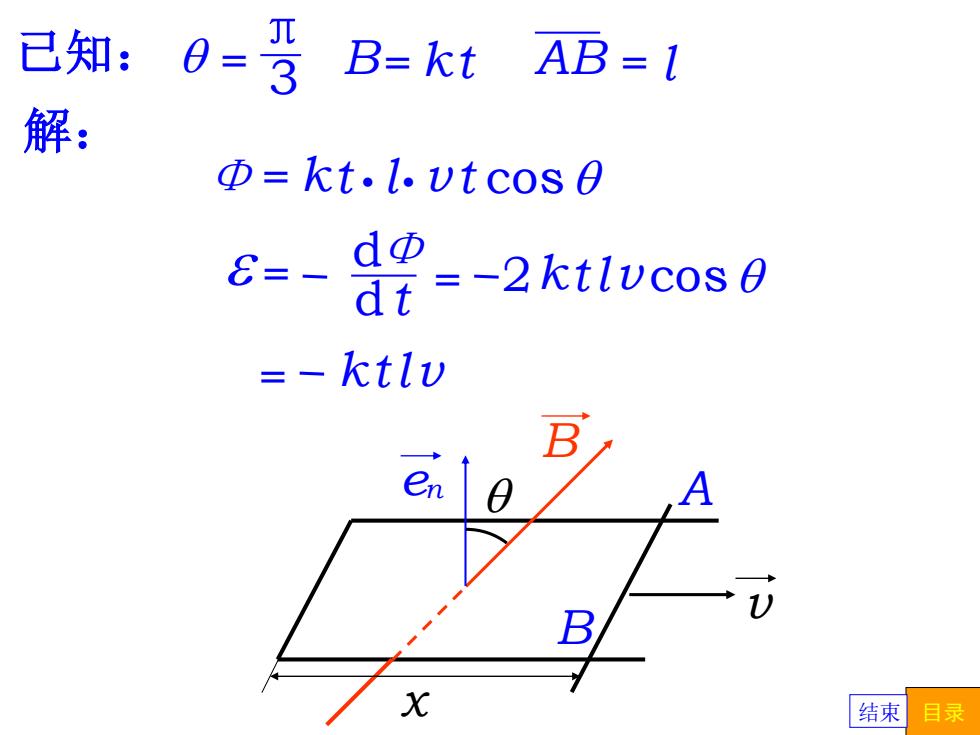
已知:0=3 B=kt」 AB=1 Φ=kt.l.vtcos 0 E=、 dΦ di =-2ktlvcos0 =ktlv L/ X 结束目录
解: 已知: π B= kt 3 q = AB = l Φ = kt.l. v t cos q d e = Φ d t = 2ktlv cos q = ktlv q A B x n v e B 结束 目录
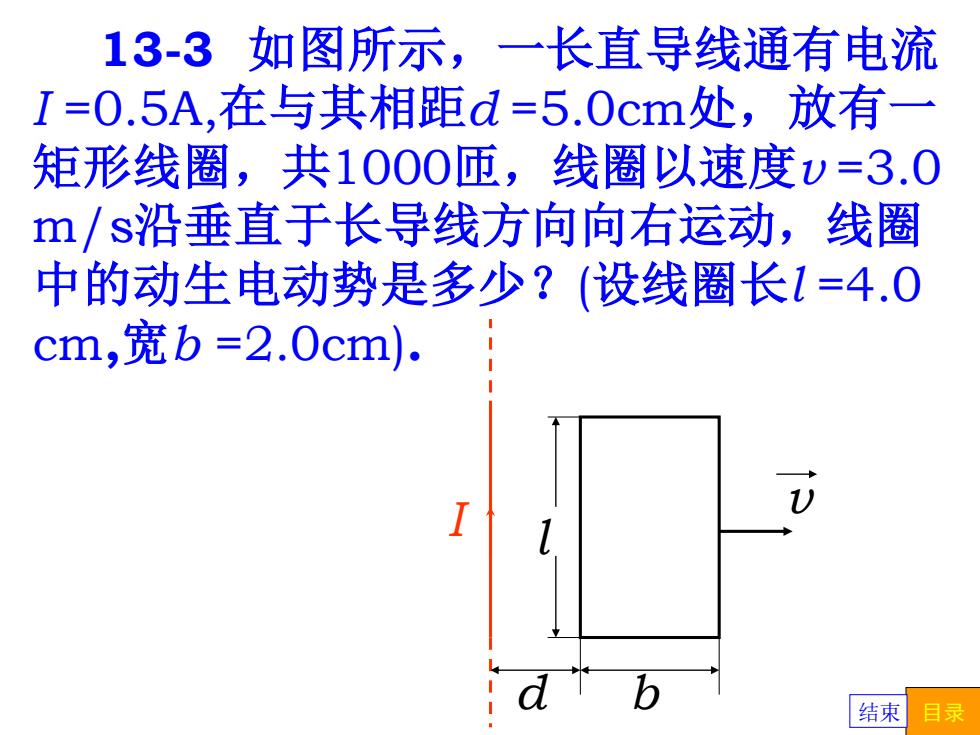
13-3如图所示,一长直导线通有电流 I=0.5A,在与其相距d=5.0cm处,放有一 矩形线圈,共1000匝,线圈以速度v=3.0 m/s沿垂直于长导线方向向右运动,线圈 中的动生电动势是多少?(设线圈长1=4.0 cm,宽b=2.0cm). 结束 目录
13-3 如图所示,一长直导线通有电流 I =0.5A,在与其相距d =5.0cm处,放有一 矩形线圈,共1000匝,线圈以速度v =3.0 m/s沿垂直于长导线方向向右运动,线圈 中的动生电动势是多少?(设线圈长l =4.0 cm,宽b =2.0cm). I v l d b 结束 目录

己知:I=0.5A,d=5.0cm,N=1000 v=3m/s,1=4.0cm,b=2.0cm 解: 8=NB1v-B1v) -Nlv 2 a3 11 g日a】 2 000x4x107x0.5x4x102x3×5x1027X10 =6.86×105(V 结束目录
已知: I =0.5A,d =5.0cm, N =1000, v =3m/s, l =4.0cm, b =2.0cm 解: e =N (B2l v B l v ) 1 2π(d+b) =N l v I 1 2πd I 1 (d+b) N l v = 2π d I 1 1 1 =1000×4π×10-7×0.5×4×10-2×3× 5×10-2 7×10-2 1 1 =6.86×10-5(V) I v l d b 结束 目录
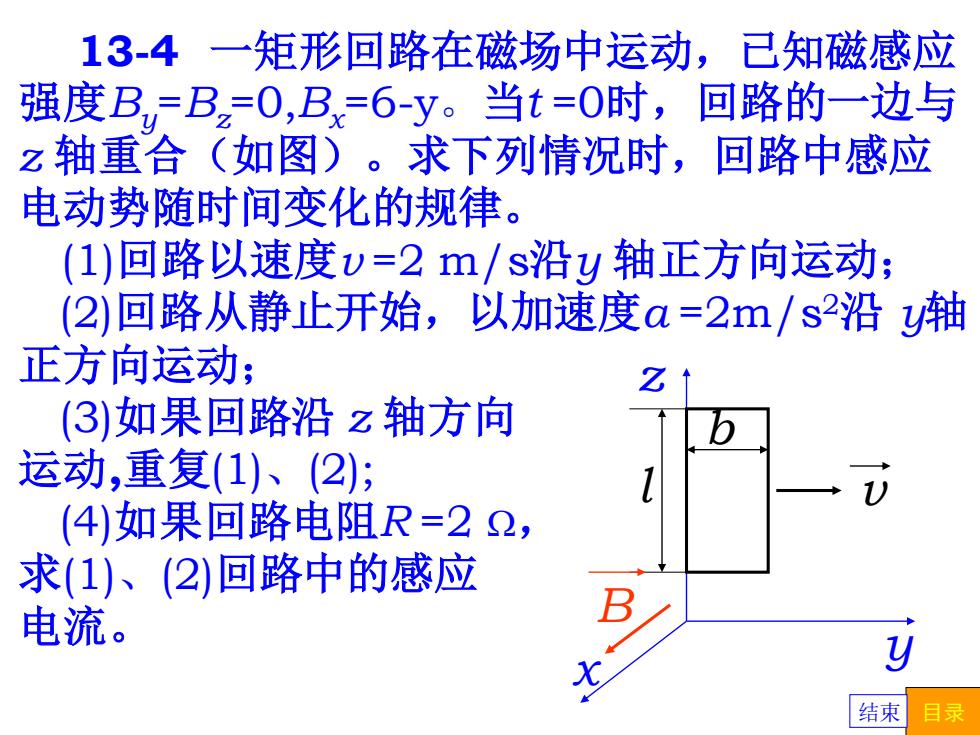
13-4一矩形回路在磁场中运动,已知磁感应 强度B,=B2=0,B=6-y。当t=0时,回路的一边与 z轴重合(如图)。求下列情况时,回路中感应 电动势随时间变化的规律。 (1)回路以速度v=2m/s沿y轴正方向运动; (2)回路从静止开始,以加速度a=2m/s2沿y轴 正方向运动; (3)如果回路沿z轴方向 运动,重复(1)、(2); (4)如果回路电阻R=22, 求(1)、(2)回路中的感应 电流。 结束 目录
13-4 一矩形回路在磁场中运动,已知磁感应 强度By =Bz=0,Bx=6-y。当t =0时,回路的一边与 z 轴重合(如图)。求下列情况时,回路中感应 电动势随时间变化的规律。 (1)回路以速度v =2 m/s沿y 轴正方向运动; (2)回路从静止开始,以加速度a =2m/s2沿 y轴 正方向运动; (3)如果回路沿 z 轴方向 运动,重复(1)、(2); (4)如果回路电阻R =2 W, 求(1)、(2)回路中的感应 电流。 B z x v y l b 结束 目录

己知:B=B2=0,Bx=6-y,v=2m/s, a=2m/s2,R=22 求:G,I 解:(1) 8=Blv-Blv =(6-yω1y-[6-(y+0.2)]1v =1w[(6-y)-(6-y-0.2)] y =1w6-y-6+y+0.2] =0.21v=0.2×0.5×2=0.2(V) 结束 目录
已知:By =Bz=0, Bx= 6-y, v = 2m/s, a = 2m/s2 , R =2W 解: e =B2l v B1l v =(6-y) l v-[6-(y+0.2)] l v = lv[ (6-y) -(6-y-0.2)] = lv[ 6-y -6+y+0.2] =0.2 lv =0.2×0.5×2 =0.2(V) (1) B z x v y l b 求:ei , I 结束 目录

(2) v=at 8=0.2V 3) 8=0 (4)I= £_0.2 R = =0.1A 结束} 目录
e =0.2t(V) = 0.2 2 =0.1t(A) (2) v = at (3) e =0 I = e R (4) 结束 目录