
刚体转动习题 焦耳 结束 习题总目录
焦耳 刚体转动习题刚体转动习题 结束 习题总目录

风刚体转动习题 4-1 4-2 4-3 4-4 4-5 4-6 4-7 4-8 4-9 4-10 -11 4-12 4-13 4-14 4-15 4-16 4-17 4-18 4-19 4-20 4-21 4-22 4-23 4-24 4-25 4-26 4-27 4-28 4-29 4-30 4-31 4-32 习题总目录 结束 目录
4-1 4-2 4-3 4-4 4-5 4-6 4-7 4-8 4-9 4-10 4-11 4-12 4-13 4-14 4-15 4-16 4-17 4-18 4-19 4-20 4-21 4-22 4-23 4-24 4-25 4-26 4-27 4-28 刚体转动习题 目录 4-29 4-30 4-31 4-32 习题总目录 结束

4-1一飞轮直径为0.30m,质量为5.00 kg,边缘绕有绳子,现用恒力拉绳子的一端, 使其由静止均匀地加速,经0.50s转速达 10r/3。假定飞轮可看作实心圆柱体,求: (1)飞轮的角加速度及在这段时间内转过 的转数; (2)拉力及拉力所作的功: (3)从拉动后经t=10s时飞轮的角速度及 轮边缘上一点的速度和加速度。 结束目录
4 -1 一飞轮直径为0.30m,质量为5.00 kg,边缘绕有绳子,现用恒力拉绳子的一端, 使其由静止均匀地加速 ,经 0.50 s 转速达 10r/3。假定飞轮可看作实心圆柱体,求: (1)飞轮的角加速度及在这段时间内转过 的转数; (2)拉力及拉力所作的功; (3)从拉动后经 t =10s时飞轮的角速度及 轮边缘上一点的速度和加速度。 结束 目录

解: J=2MR2-5x1g15-5.2x102k3m2 2 (1)w=2Tn=t ω2n2×3.14×10 a=t= t 0.5 =1.26×1021/s2 0= 1ut2-号×1.26×102×0.52=5m N=2=2.5rev 结束目录
5.2×10-2 kg.m2 = =1.26×102 1/s2 = = = ω a t 2πn t 2×3.14×10 0.5 1.26×102×(0.5)2 = 5π 2 1a t 2 q = = 2 1× N= q 2π = 2.5rev (1) ω= 2πn=a t 2 5 0.15 J MR 2 2 1 × = = ( ) 解: 2 结束 目录

(2) M-Ja-FR F= Ja 5.6×102×1.26×102_47N R 0.15 A-MO-FRO =47×0.15×5=111J 结束目录
= = a F R J = 5.6×10-2×1.26×102 0.15 47N A =Mq =FRq =47×0.15×5π=111J (2) M= J a =FR 结束 目录

(3)w=0t =1.26×102×10=1.26×1031/s v=Rw=0.15×1.26×103 =1.89×102m/s an=Rw2=0.15×(1.26×103)2 =2.38×105m/s2 at=R0=0.15X1.26X102 =18.9m/s2 结束目录
v=Rω= 0.15×1.26×103 =1.89×102 m/s at = Ra = 0.15×1.26×102 an 2 = Rω = 0.15×(1.26×103) 2 =2.38×105 m/s2 =1.26×102×10=1.26×103 1/s (3) ω =a t =18.9m/s2 结束 目录

4-2飞轮的质量为60kg,直径为0.50m 转速为1000r/min,现要求在5s内使其制 动,求制动力F,假定闸瓦与飞轮之间的摩擦 系数u=0.4,飞轮的质量全部分布在轮的外 周上。尺寸如图所示。 0.5m 0.75m 闸瓦 结束目录
4-2 飞轮的质量为60kg,直径为0.50m, 转速为1000r/min,现要求在 5s内使其制 动,求制动力 F ,假定闸瓦与飞轮之间的摩擦 系数μ= 0.4,飞轮的质量全部分布在轮的外 周上。尺寸如图所示。 F 闸瓦 d ω 0.5m 0.75m 结束 目录

解:J=mR2=60×(0.25)2 N =3.75kg.m2 t=0w。=2mn=2L×1000 60 =104.7r/s t=5ω=0 0= 0-104.7-20.9r/s2 5 F(l1+12)-N1=0 fR=Ja=HNR N=Ja uR F二1 4,聚=314N 1+12R 结束目录
=3.75kg.m2 t =0 1000 60 ω0 = 2πn= 2π× =104.7 r/s t =5 ω =0 f N N F f l 1 l 2 J mR 2 = = 60×(0.25) 解: 2 ω 104.7 20.9 r/s2 5 0 a t = = = ω0 F (l 1 + l 2) N l 1= 0 f R= J a = m NR l 1 F = l 1 + l 2 mR J a = 314N m N = R J a 结束 目录
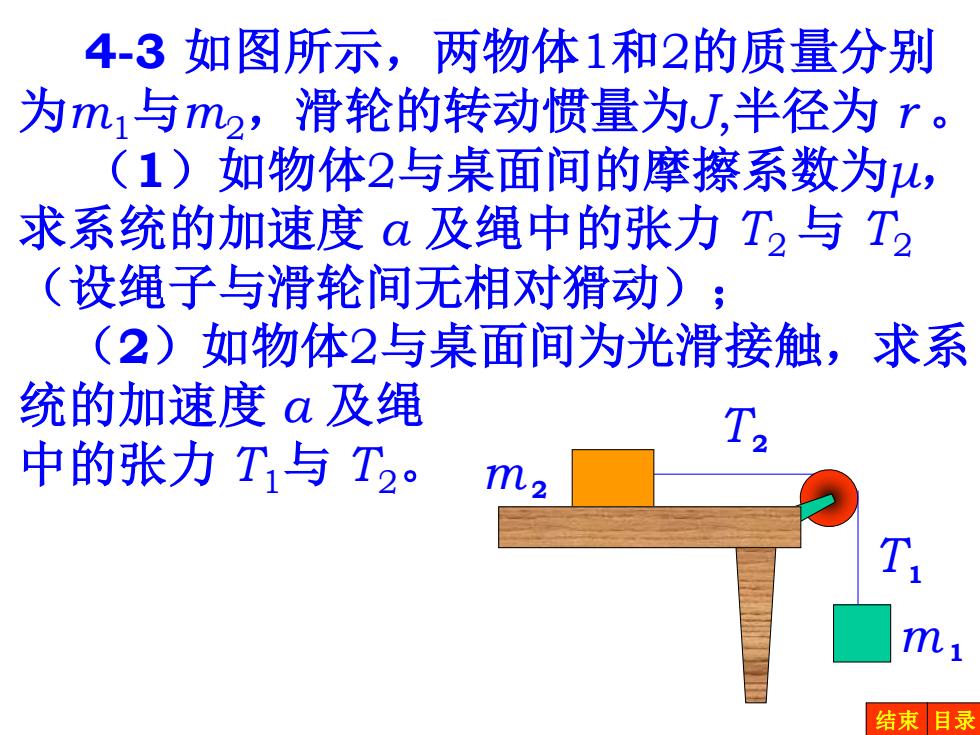
4-3如图所示,两物体1和2的质量分别 为m1与m2,滑轮的转动惯量为U,半径为r。 (1)如物体2与桌面间的摩擦系数为u, 求系统的加速度α及绳中的张力T2与T2 (设绳子与滑轮间无相对猾动); (2)如物体2与桌面间为光滑接触,求系 统的加速度a及绳 中的张力T与T2 m 结束目录
4-3 如图所示,两物体1和2的质量分别 为m1与m2,滑轮的转动惯量为J,半径为 r 。 (1)如物体2与桌面间的摩擦系数为μ, 求系统的加速度 a 及绳中的张力 T2 与 T2 (设绳子与滑轮间无相对猾动); (2)如物体2与桌面间为光滑接触,求系 统的加速度 a 及绳 中的张力 T1与 T2。 m2 T2 T1 m1 结束 目录
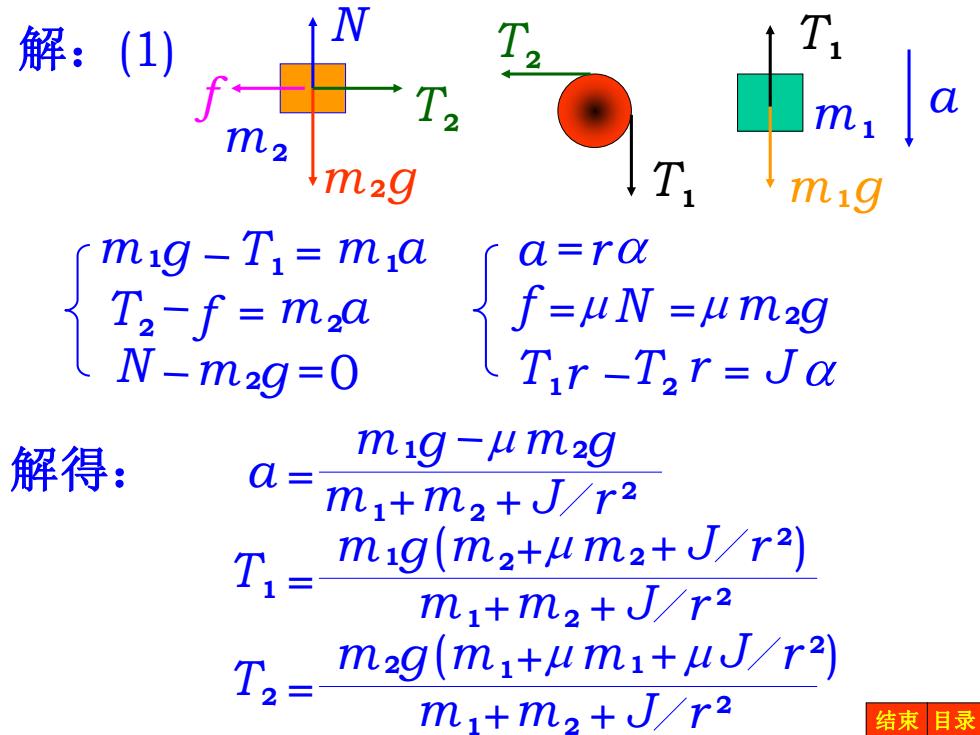
解:(1) f中 T2 m2 m m2g T. (mig -T,=ma a=ra T2-f=ma f=N=μm2g (N-m2g=0 Tr-Tar=Ja 解得: mig-um2g a=mi+ma+J/r2 刃、 mgm2+um2+J/r2) m1+m2+J/r2 m2g(mitumi+uJ/r2 mi+m2+/r2 结束目录
f =m N =m m2g m1g T1 = m1a T2 f = m2a a =ra + = r 2 m1g (m2 m m2+ J ) r 2 m1+m2 + J T1 + = r 2 m2g (m1 m m1+ J ) r 2 m1+m2 + J T2 m N g f T2 m2 m2 T2 T1 a m1g T1 m1 N m2g =0 T1r T2 r = J a r 2 + + a = m1g m m2g m1 m2 J 解得: 解:(1) 结束 目录