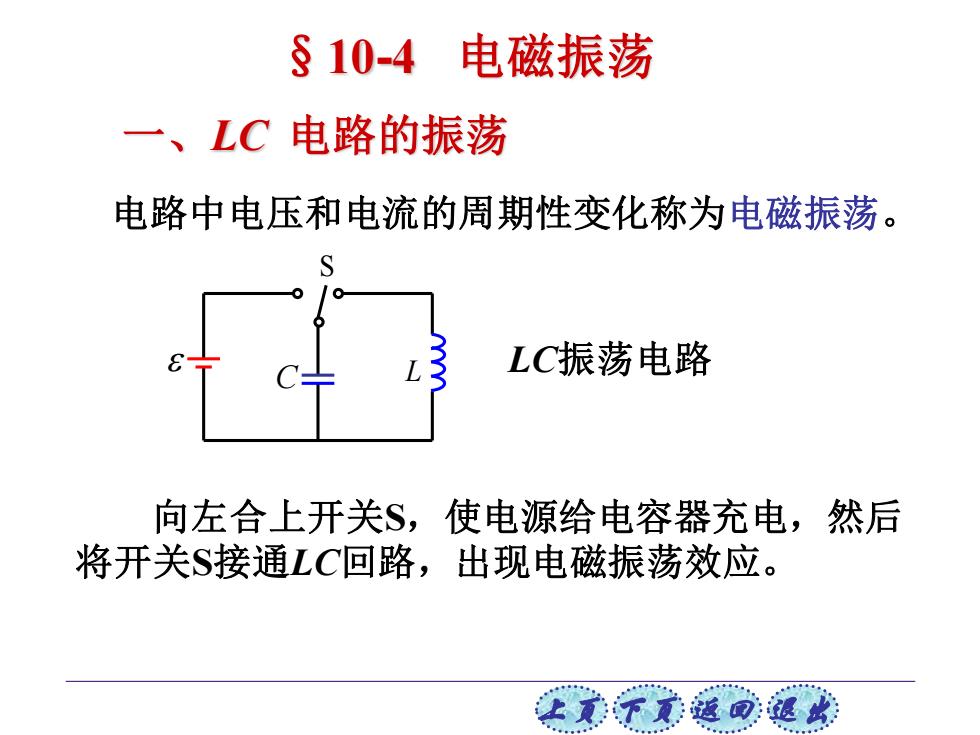
§10-4 电磁振荡 一、LC电路的振荡 电路中电压和电流的周期性变化称为电磁振荡。 LC振荡电路 向左合上开关S,使电源给电容器充电,然后 将开关S接通LC回路,出现电磁振荡效应。 让美下觉返司速此
上页 下页 返回 退出 电路中电压和电流的周期性变化称为电磁振荡。 C L S LC振荡电路 向左合上开关S,使电源给电容器充电,然后 将开关S接通LC回路,出现电磁振荡效应。 §10-4 电磁振荡 一、LC 电路的振荡
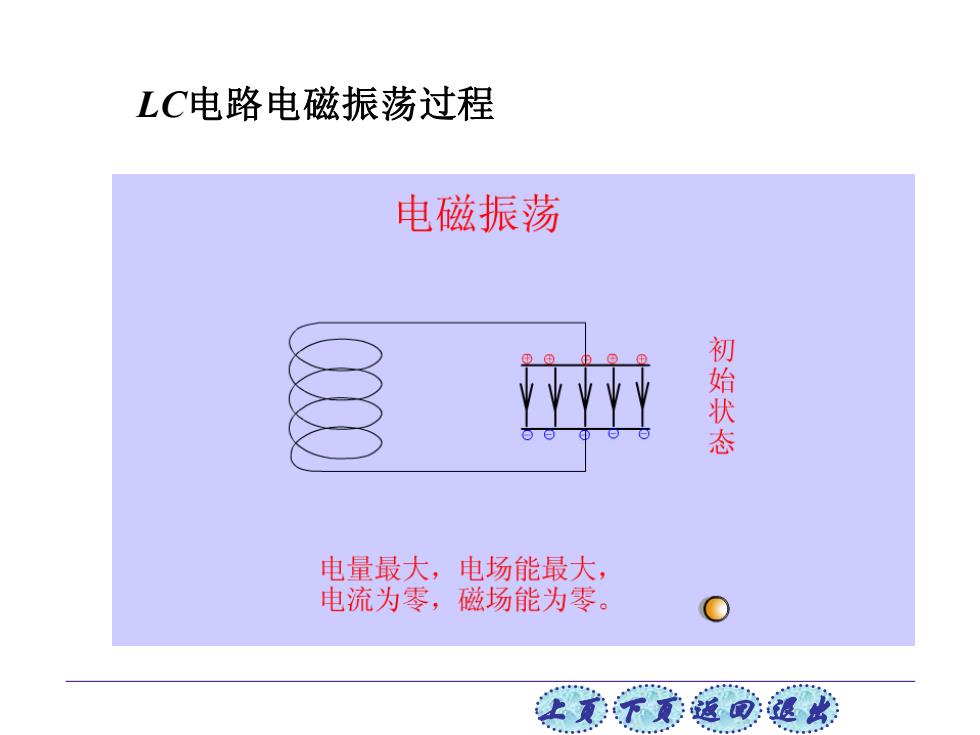
LC电路电磁振荡过程 电磁振荡 初始状态 电量最大,电场能最大, 电流为零,磁场能为零。 女贰不京返可退此
上页 下页 返回 退出 LC电路电磁振荡过程
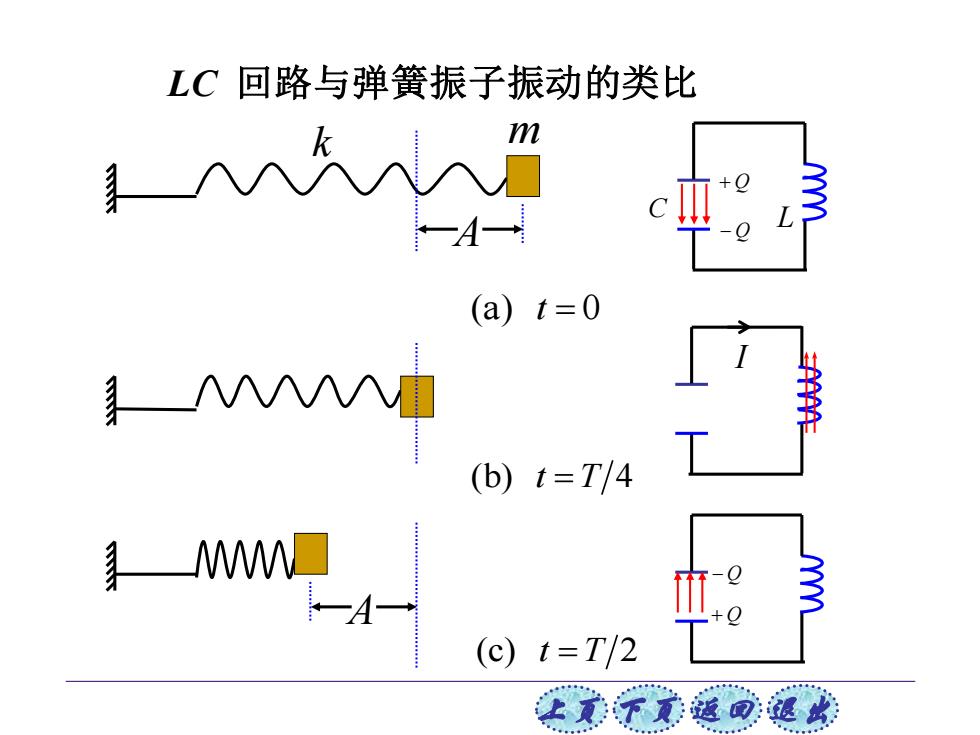
LC回路与弹簧振子振动的类比 (a)t=0 -MNM (b)t=T/4 W□ 一A (c)t=T/2 王觉下元菠面:退收
上页 下页 返回 退出 LC 回路与弹簧振子振动的类比 (a) 0 t = k m (b) 4 t T= L C + Q − Q (c) 2 t T= A − Q + Q I A
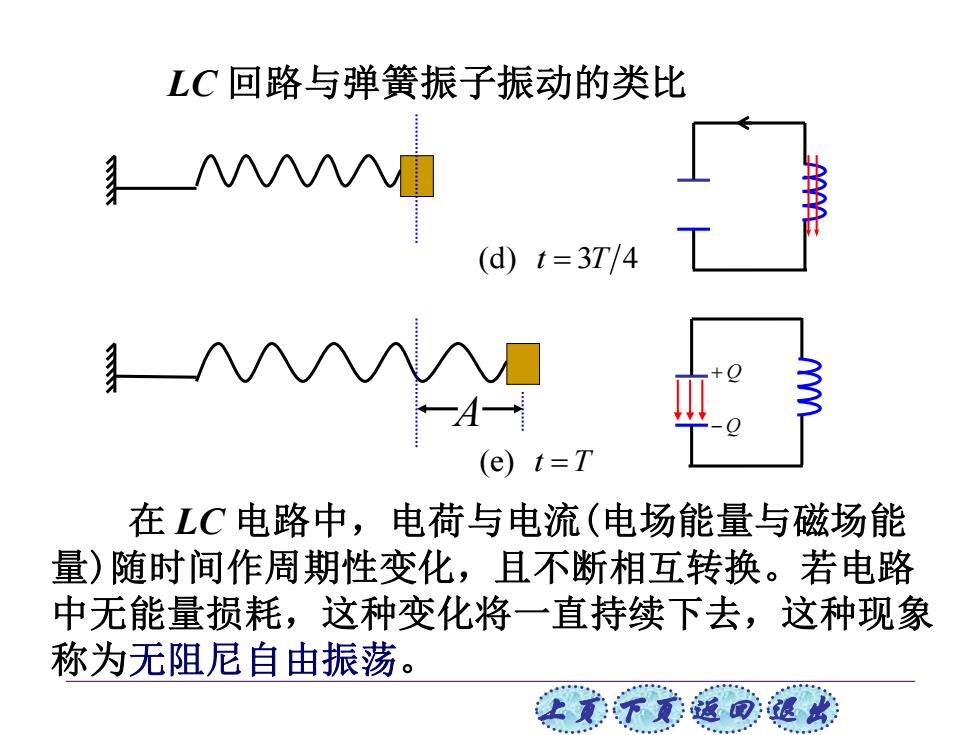
LC回路与弹簧振子振动的类比 I (d)t=3T/4 (e)t=T 在LC电路中,电荷与电流(电场能量与磁场能 量)随时间作周期性变化,且不断相互转换。若电路 中无能量损耗,这种变化将一直持续下去,这种现象 称为无阻尼自由振荡。 上贰返退
上页 下页 返回 退出 LC 回路与弹簧振子振动的类比 (d) 3 4 t T = (e) t T= A − Q + Q 在 LC 电路中,电荷与电流(电场能量与磁场能 量)随时间作周期性变化,且不断相互转换。若电路 中无能量损耗,这种变化将一直持续下去,这种现象 称为无阻尼自由振荡

设某一时刻电容器极板上电量为9,电路中电流为i, 取LC回路的顺时针方向为电流正向,得到 di =9i=- dq (因dq<0) dt dt )q=Qcos(ot+4)) 2o是电荷振幅,中,是振荡初相,均由初始条件确定。 LC回路自由振荡角频率o2=1/LC V= T=2π√LC 2πVLC 让美觉返司退
上页 下页 返回 退出 设某一时刻电容器极板上电量为q,电路中电流为i, 取LC 回路的顺时针方向为电流正向,得到 , d d C q t i L = t q i d d = − (因 d q 0 ) q t LC q 1 d d 2 2 = − 2 cos( ) = 0 +0 q Q t LC 回路自由振荡角频率 1 LC 2 = T LC = 2π 1 2π LC = Q0是电荷振幅, 0 是振荡初相,均由初始条件确定

将电量表达式对时间求导,得到电流表达式: i= da,sin(o c) dt 其中I,=⊙Q为电流振幅。 从上述分析结果可知,电量和电流都作简谐振动。 而且电荷和电流的振荡频率相同,电流的相位比电荷 的相位超前), 如下图所示: 女意不意通可退此
上页 下页 返回 退出 将电量表达式对时间求导,得到电流表达式: 0 Q0 其中 I = 为电流振幅。 从上述分析结果可知,电量和电流都作简谐振动。 0 0 0 0 d sin( ) cos( ) d 2 q i Q t I t t = = − + = + + 而且电荷和电流的振荡频率相同,电流的相位比电荷 的相位超前 π 2 ,如下图所示: t o 0 I Q0

设t时刻电容器极板上电量为g,相应的电场能量为 dcos'(o+ 2c 2C 此刻电流为,则线圈中的磁场能量为 an(o) 将电场和磁场能量相加,并利用o2=1/LC,得 所=所+g= 2c 上式表明,尽管电能和磁能均随时间变化,但 总能量守恒。 让意文返可退攻
上页 下页 返回 退出 将电场和磁场能量相加,并利用 1 LC ,得 2 = 上式表明,尽管电能和磁能均随时间变化,但 总能量守恒。 设t 时刻电容器极板上电量为q,相应的电场能量为 此刻电流为i,则线圈中的磁场能量为 2 2 0 2 e 0 cos ( ) 2 2 q Q W t C C = = + 2 2 2 2 0 m 0 1 sin ( ) 2 2 L Q W Li t = = + 2 0 e m 2 Q W W W C = + =
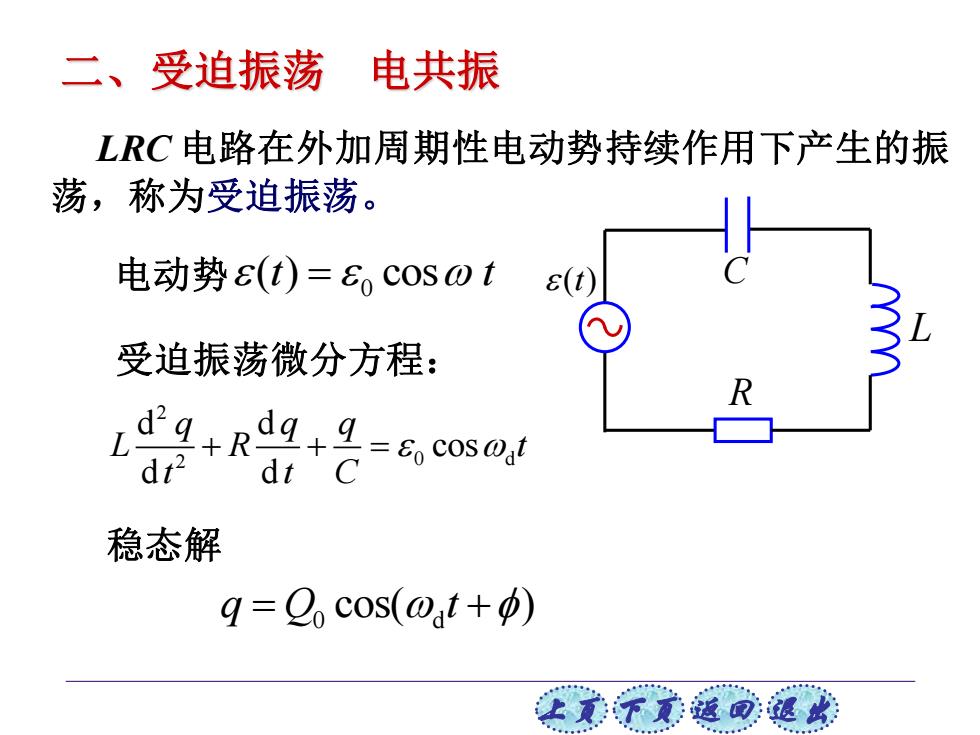
二、受迫振荡 电共振 LRC电路在外加周期性电动势持续作用下产生的振 荡,称为受迫振荡。 电动势&(t)=oc0S0t (t) 受迫振荡微分方程: dig+Rdg+9-Cos@ L d12 dt C 稳态解 q-C cos(@at+o) 上意不家道可退欢
上页 下页 返回 退出 LRC 电路在外加周期性电动势持续作用下产生的振 荡,称为受迫振荡。 受迫振荡微分方程: 稳态解 二、受迫振荡 电共振 L C R 电动势 ( )t 0 ( ) cos t t = 2 2 0 d d d cos d d q q q L R t t t C + + = 0 d q Q t = + cos( )

q =2o cos(@jt+o) 2〉, dg=-sin=+ 其中 Eo 0= an4's②C,l R oL为感抗, 为电抗, 0 为容抗,D工一 t-c) 为阻抗 让美觉返司退
上页 下页 返回 退出 其中 L 为感抗, 1 L C − 为电抗, 0 d q Q t = + cos( ) 0 d 0 d 0 d sin( ) cos( ') d q i Q t I t t = = − + = + 0 0 2 2 d d 1 I R L C = + − d d 0 1 tan ' L C R − = 为容抗, 1 C 为阻抗 2 2 1 R L C + −

当电路满足L-C 时, 电流振幅最大 R 周期性电动势作用下,电流振幅达到最大值 电共振 上美不意道可退欢
上页 下页 返回 退出 0 R 周期性电动势作用下,电流振幅达到最大值 电共振 当电路满足 d d 1 L C = 电流振幅最大 即 d 1 LC = 时