《普通物理学》课程教学资源（PPT课件）第十二章 几何光学 12-8 单缝的夫琅禾费衍射

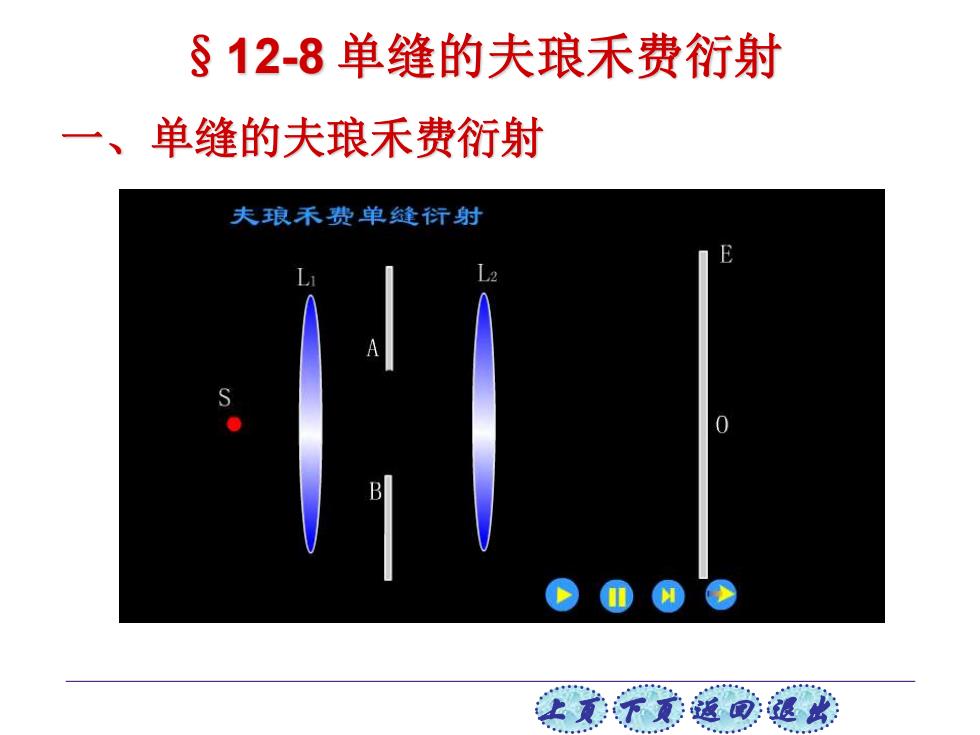
§12-8单缝的夫琅禾费衍射 一、单缝的夫琅禾费衍射 夫琅禾费单缝衍射 让美觉返司退

上页 下页 返回 退出 §12-8 单缝的夫琅禾费衍射 一、单缝的夫琅禾费衍射

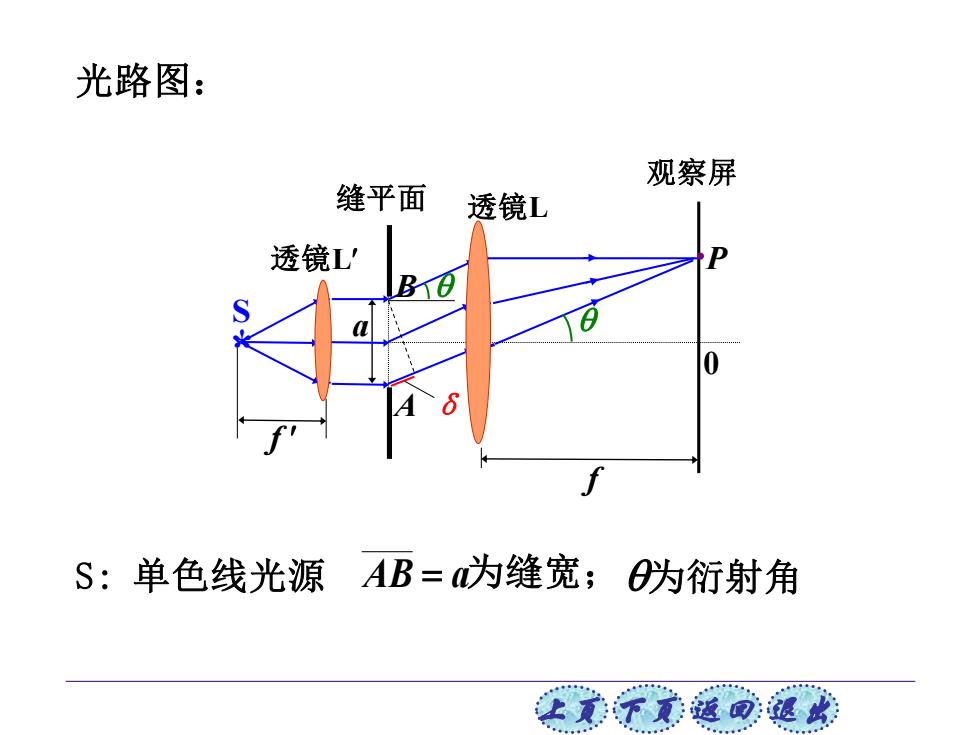
光路图： 观察屏 缝平面 透镜L 透镜L B日 S:单色线光源AB=为缝宽；为衍射角 之美齐家道司退欢

上页 下页 返回 退出 S: 单色线光源 AB = a 为缝宽； * S f f  a   透镜L 透镜L ·P A B 缝平面 观察屏 0 δ 为衍射角 光路图：

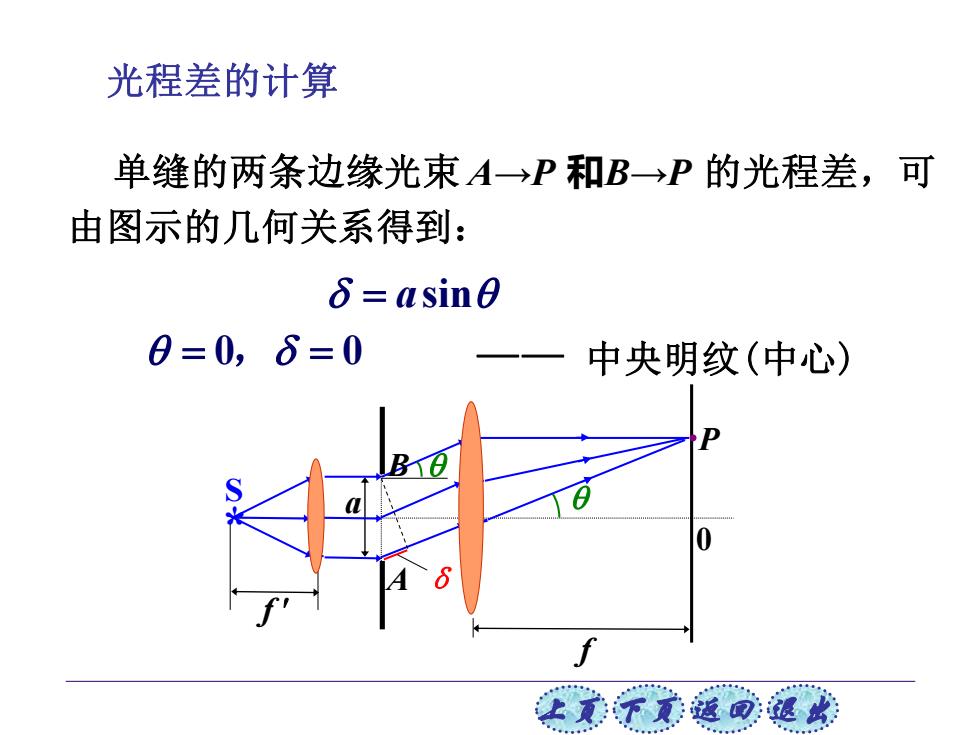
光程差的计算 单缝的两条边缘光束A→P和BP的光程差，可 由图示的几何关系得到： δ=asin0 0=0,8=0 中央明纹（中心） 让美觉返司退

上页 下页 返回 退出  = asin  = 0， = 0 —— 中央明纹(中心) 单缝的两条边缘光束 A→P 和B→P 的光程差，可 由图示的几何关系得到： * S f f  a   ·P A B 0 δ 光程差的计算

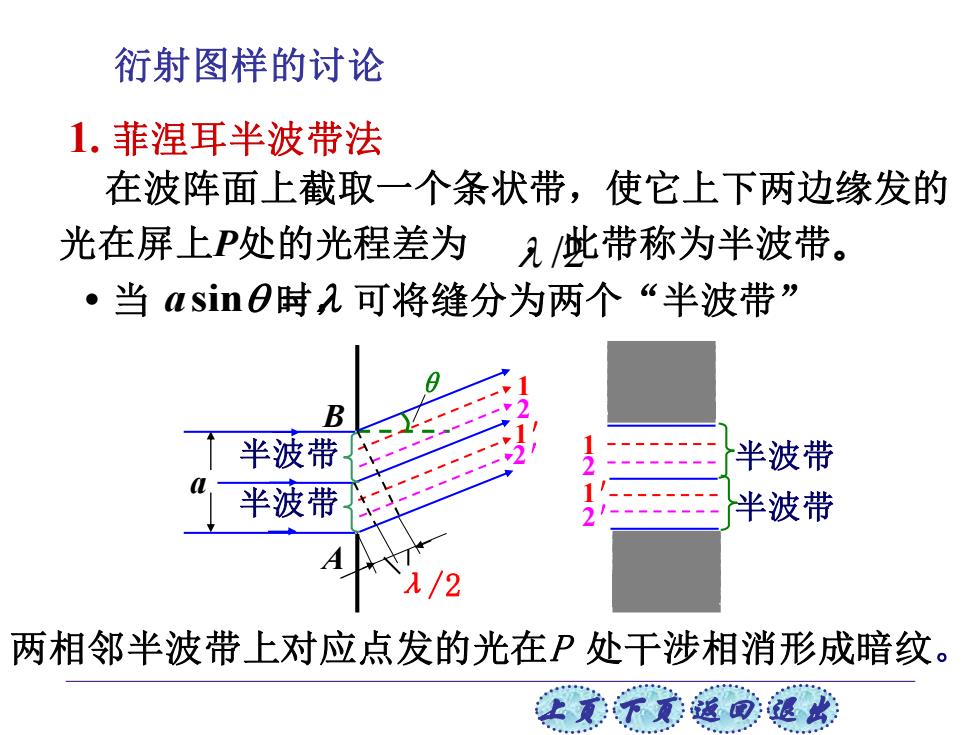
衍射图样的讨论 1.菲涅耳半波带法 在波阵面上截取一个条状带，使它上下两边缘发的 光在屏上P处的光程差为 九此带称为半波带。 ·当asinO时孔可将缝分为两个“半波带” B 半波带 半波带 半波带 半波带 λ/2 两相邻半波带上对应点发的光在P处干涉相消形成暗纹。 让意不意返回这攻

上页 下页 返回 退出 a θ 1′ B 2 A 半波带 半波带 1 2′ 两相邻半波带上对应点发的光在P 处干涉相消形成暗纹。 λ/2 半波带 半波带 1 2 1′ 2′  当 asin 时 = ，  可将缝分为两个“半波带” 1. 菲涅耳半波带法 在波阵面上截取一个条状带，使它上下两边缘发的 光在屏上P处的光程差为 ，此带称为半波带 /2 。 衍射图样的讨论

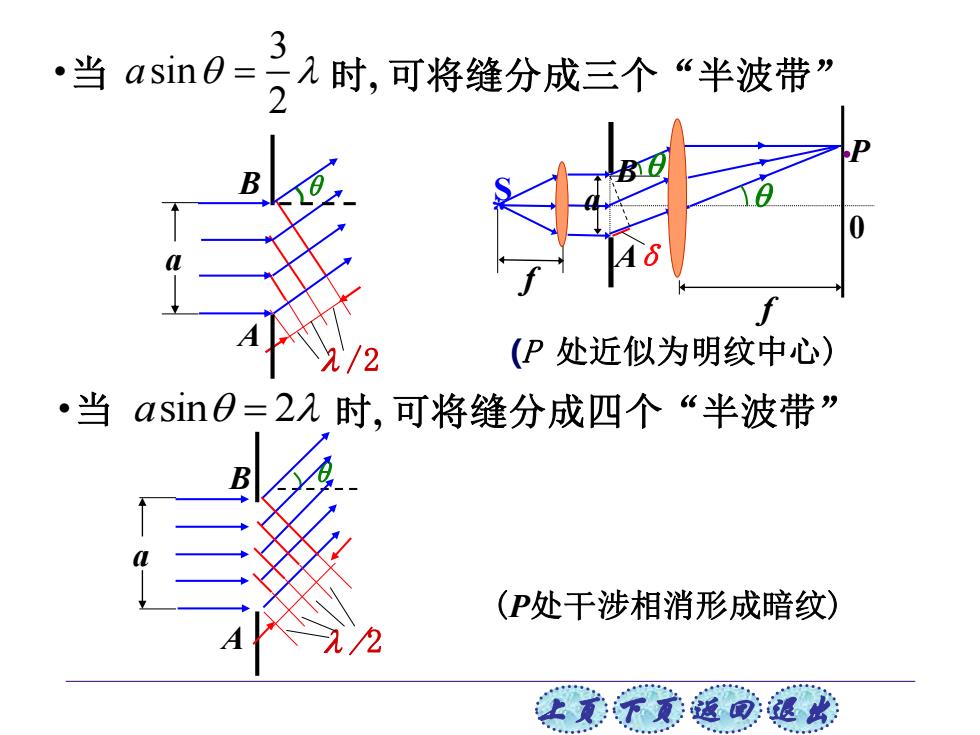
3 asin8=2入时，可将缝分成三个“半波带” 当 (P处近似为明纹中心) 当 asin0=22时，可将缝分成四个“半波带” (P处干涉相消形成暗纹) 让美下觉返司速此

上页 下页 返回 退出 (P 处近似为明纹中心) a  /2 B θ A a B A θ  /2 (P处干涉相消形成暗纹) * S f f a   ·P A B 0 δ •当 3 sin 2 a   = 时, 可将缝分成三个“半波带” •当 asin 2   = 时, 可将缝分成四个“半波带

2.明暗纹条件 由半波带法可得明暗纹条件为： asin0=±2k ，k=12,3,.-—暗纹 2 asin6=±(2k+1)7k=1,23,. 明纹（中心） asin=0 中央明纹（中心） 上述暗纹和中央明纹（中心）的位置是准确的，其余 明纹中心的实际位置较上稍有偏离

上页 下页 返回 退出 暗纹 明纹 中心 中央明纹 中心 上述暗纹和中央明纹(中心)的位置是准确的，其余 明纹中心的实际位置较上稍有偏离。 2.明暗纹条件 由半波带法可得明暗纹条件为： sin 2 1 2 3 2 a k k   =  = ， ， sin 2 1 2 3 ( ) 2 a k k   =  + = 1 ， ， asin 0  =

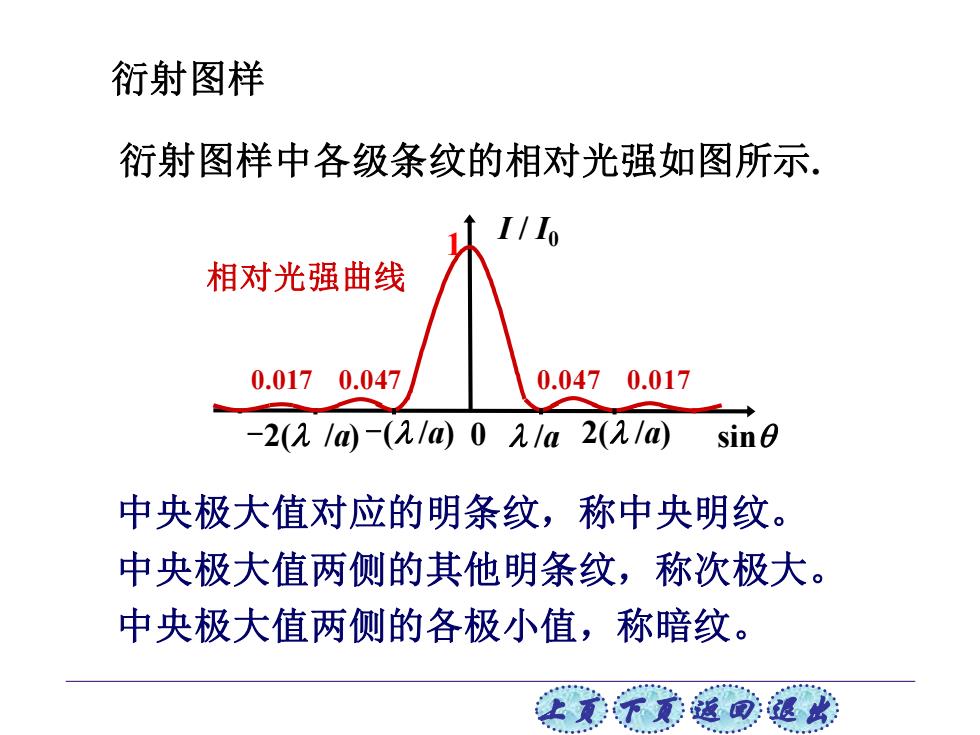
衍射图样 衍射图样中各级条纹的相对光强如图所示， I/Io 相对光强曲线 0.0170.047 0.0470.017 -2(2/)-(21@0元1a2(2/@ sin 中央极大值对应的明条纹，称中央明纹。 中央极大值两侧的其他明条纹，称次极大。 中央极大值两侧的各极小值，称暗纹。 让美下觉返司速此

上页 下页 返回 退出 衍射图样 衍射图样中各级条纹的相对光强如图所示. -2( /a) -( /a)  /a 2( /a) 0.047 0.017 1 I / I0 0 相对光强曲线 0.017 0.047 sin 中央极大值对应的明条纹，称中央明纹。 中央极大值两侧的其他明条纹，称次极大。 中央极大值两侧的各极小值，称暗纹

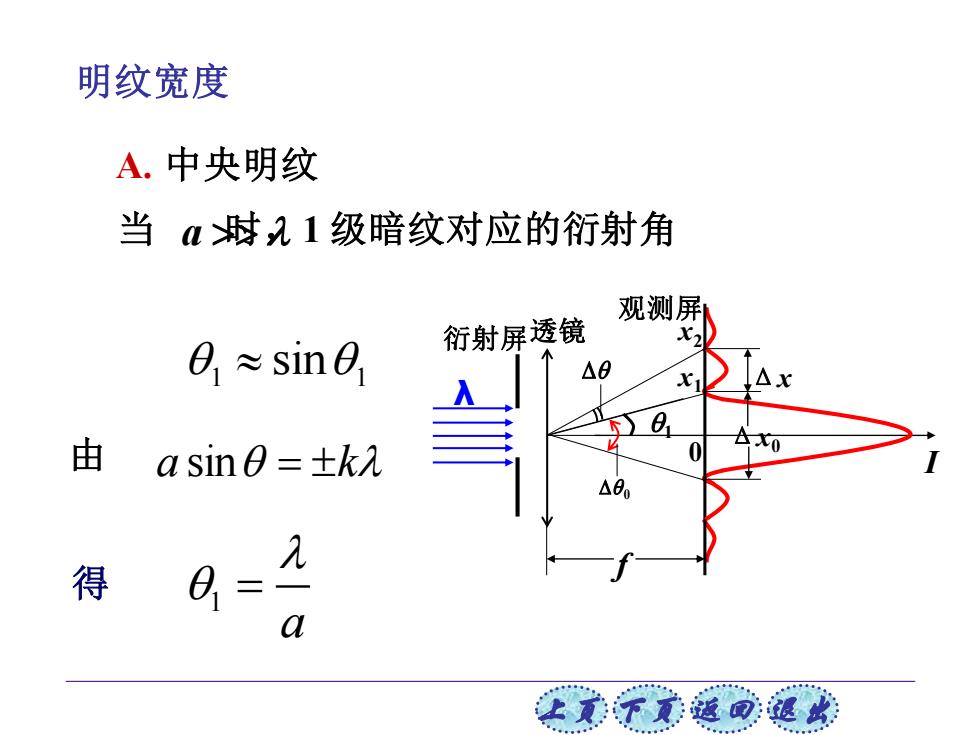
明纹宽度 A.中央明纹 当a时21级暗纹对应的衍射角 观测屏 e,≈sin 衍射屏透镜 X2 △8 由 asin0=±k入 得 a 上美不家返可退此

上页 下页 返回 退出 明纹宽度 λ Δx I 0 x1 衍射屏透镜 x2 观测屏 Δx0 f 1  0  A. 中央明纹 当 a  时，  1 级暗纹对应的衍射角 由 a sin = k 1 1   sin 得 1 a   =

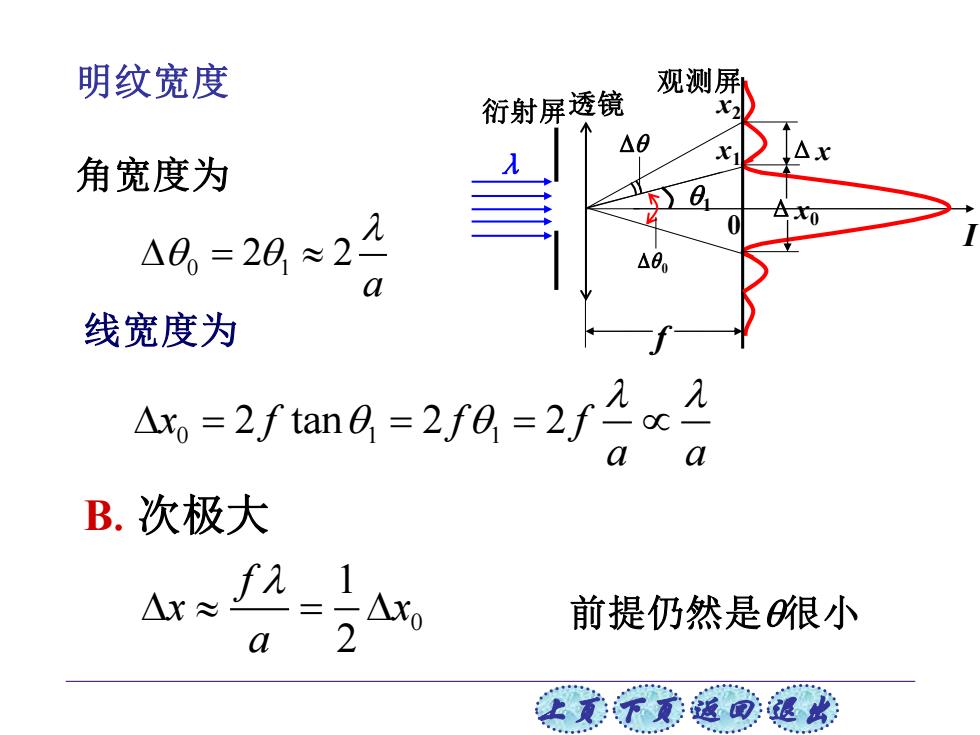
明纹宽度 观测屏 衍射屏透镜 △8 角宽度为 △0=20≈2 △8 a 线宽度为 -2fm0-2fA-2/合8 B.次极大 Ar≈A 1 前提仍然是很小 a 2 让式不元通司：退

上页 下页 返回 退出 角宽度为 线宽度为 λ Δx I 0 x1 衍射屏透镜 x2 观测屏 Δx0 f 1  0  B.次极大 前提仍然是很小 明纹宽度 0 1 2 2 a   =    0 1 1 x f f f 2 tan 2 2 a a    = = =    0 1 2 f x x a    = 

缝宽变化对条纹的影响 由 △x≈ fA 1 2 a 知，缝宽越小，条纹宽度越宽 sin0 当元/a时，p0 △x=0，此时屏幕呈一片明亮； 当元/a时，0 ，做时屏幕上只显出单 一的明条纹一一单缝的几何光学像。 故，几何光学是波动光学在/0时的极限情形

上页 下页 返回 退出 缝宽变化对条纹的影响 知，缝宽越小，条纹宽度越宽 ，此时屏幕呈一片明亮； I 0 sin 故，几何光学是波动光学在/a→0时的极限情形。 ， 此时屏幕上只显出单 一的明条纹——单缝的几何光学像。 当  a → 时， 0 当  a → 时，  由 0 1 2 f x x a    =  =  x  →x 0