
§13-4氢原子光谱玻尔的氢原子理论 *一、氢原子光谱的规律性 原子发光是重要的原子现象之一,光谱学的 数据对物质结构的研究具有重要意义。 氢原子谱线的波长可以用下列经验公式表示: =R( k=1,232. n=k+1,k+2,k+3,. = λ 波数 R=1.096776×107m1里德伯常量 让元子文返回退此
上页 下页 返回 退出 原子发光是重要的原子现象之一,光谱学的 数据对物质结构的研究具有重要意义。 氢原子谱线的波长可以用下列经验公式表示: 2 2 1 1 R( ) k n = − k =1,2,3, n = k +1,k + 2,k + 3, 7 1 R 1.096776 10 m− = 里德伯常量 1 ~ = 波数 *一、氢原子光谱的规律性 §13-4 氢原子光谱 玻尔的氢原子理论
巴耳末系 莱曼系 波长0.8 0.6 0.4 0.20m 可见光紫外线 普丰德系 布拉开系 帕邢系 5.0 4.0 3.02.0 1.04m 红 外 线 让美觉返司退
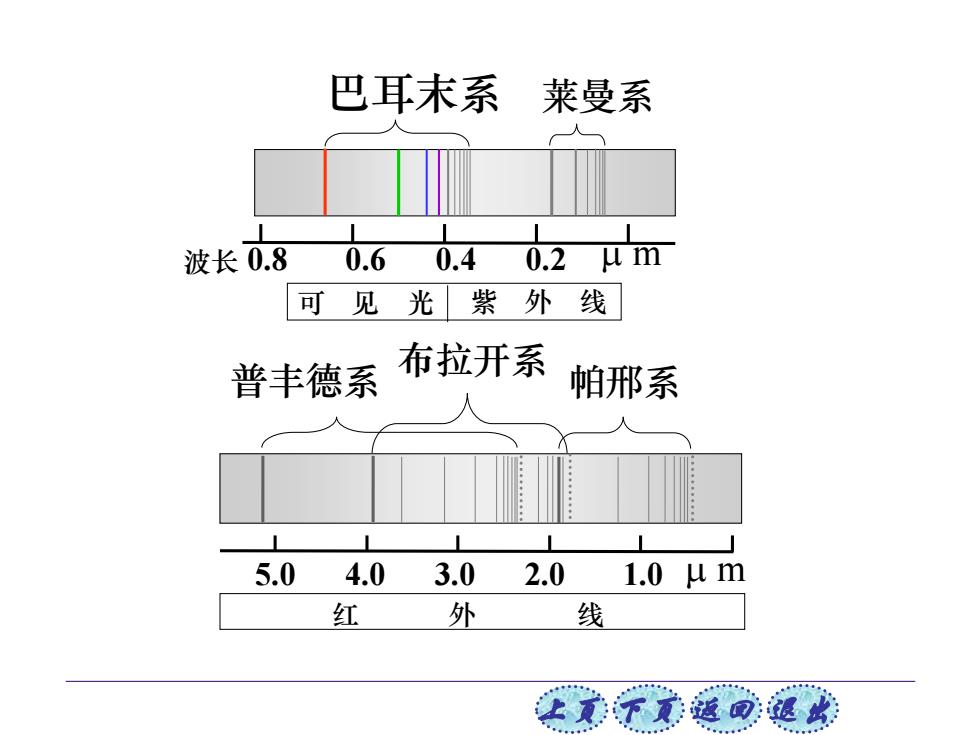
上页 下页 返回 退出 巴耳末系 莱曼系 波长 0.8 0.6 0.4 0.2 m m 可 见 光 紫 外 线 布拉开系 帕邢系 5.0 4.0 3.0 2.0 1.0 m m 红 外 线 普丰德系

k=1,n=2,3,. 莱曼系,紫外区 k=2,n=3,4,. 巴耳末系,可见光区 k=3,n=4,5,. 帕邢系,红外区 k=4,n=5,6,. 布拉开系,红外区 k=5,n=6,7,. 普丰德系,红外区 k=6,n=7,8,.哈弗莱系,红外区 其他元素的光谱也有类似的规律性。 原子光谱线系的规律性深刻地反映了原子内部的规律性
上页 下页 返回 退出 k n = = 1, 2,3, 莱曼系,紫外区 k = 2,n = 3,4, 巴耳末系,可见光区 k = 3,n = 4,5, 帕邢系,红外区 k = 4,n = 5,6, 布拉开系,红外区 k = 5,n = 6,7, 普丰德系,红外区 k = 6,n = 7,8, 哈弗莱系,红外区 其他元素的光谱也有类似的规律性。 原子光谱线系的规律性深刻地反映了原子内部的规律性

二、玻尔的氢原子理论 1.定态假设 原子系统只能处在一系列不连续 的能量状态,在这些状态中,电子虽然作加速 运动,但并不辐射电磁波,这些状态称为原子 的稳定状态(简称定态),相应的能量分别 为E1,E2,E3, 2.频率条件当原子从一个能量为E,的定态跃迁 到另一能量为E的定态时,就要发射或吸收一个 频率为Vm的光子。 E-E& V 玻尔频率公式 让美觉返司退
上页 下页 返回 退出 1.定态假设 原子系统只能处在一系列不连续 的能量状态,在这些状态中,电子虽然作加速 运动,但并不辐射电磁波,这些状态称为原子 的稳定状态(简称定态),相应的能量分别 为 E1 ,E2 ,E3 , 。 2.频率条件 当原子从一个能量为 的定态跃迁 到另一能量为 的定态时,就要发射或吸收一个 频率为 的光子。 En Ek kn n k kn E E h − = 玻尔频率公式 二、玻尔的氢原子理论

3量子化条件在电子绕核作圆周运动中,h 其稳定状态必须满足电子的角动量L等于2元 的整数倍的条件。 h 角动量 L=n,n=1,2,3,. 2元 量子化 n为量子数 三、氢原子轨道半径和能量的计算 根据电子绕核作圆周运动的模型及角动量 量子化条件可以计算出氢原子处于各定态时的 电子轨道半径
上页 下页 返回 退出 3.量子化条件 在电子绕核作圆周运动中, 其稳定状态必须满足电子的角动量 等于 的整数倍的条件。 L 2π h , 1, 2,3, 2 h L n n = = n 为量子数 根据电子绕核作圆周运动的模型及角动量 量子化条件可以计算出氢原子处于各定态时的 电子轨道半径。 角动量 量子化 三、氢原子轨道半径和能量的计算

=n( ),n=1,2,3,. n me 玻尔半径 5=0.529×10-10m· 电子处在半径为广的轨道上运动时,可以计 算出氢原子系统的能量E为 E= m-儿23. 1 me 能量是量子化的 n=1,E,=-13.6eV,基态能级; n>1的各稳定态称为受激态; n-→o0时,n→0,En→0,能级趋于连续。 让美觉返司退
上页 下页 返回 退出 10 1 r 0.529 10 m − = 电子处在半径为 的轨道上运动时,可以计 算出氢原子系统的能量 为 n r En 能量是量子化的 玻尔半径 2 2 0 2 ( ), 1, 2,3, n h r n n me = = π 4 2 2 2 0 1 ( ), 1, 2,3, 8 n me E n n h = − = n n → 时, r → ,E n →0, 能级趋于连续。 n E = = − 1, 13.6 1 eV ,基态能级; n 1 的各稳定态称为受激态;
氢原子能级 n=0.- n=5 n=4 普丰德系 布拉开系 n=3 帕邢系 n=2-0 巴耳末系 n=1 莱曼系 正元下元道回退此
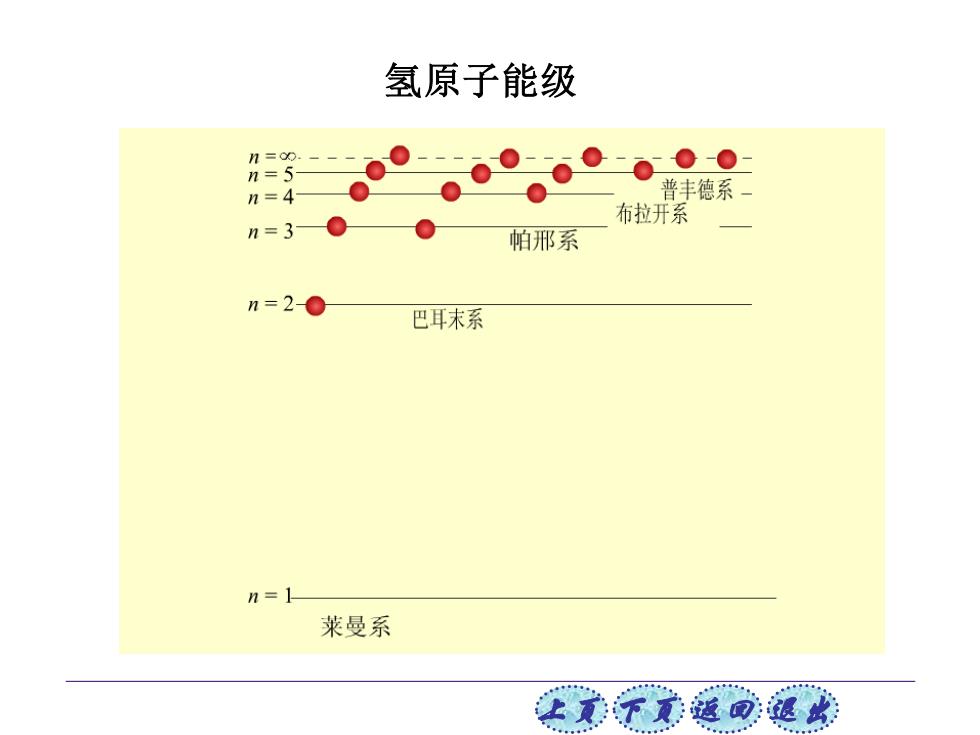
上页 下页 返回 退出 氢原子能级

根据氢原子的能级及玻尔假设,可以得到氢 原子光谱的波数公式 me4 88,2hc 与氢原子光谱经验公式是一致的。 me R= -=1.0973731×107m1 R理论值与实验值符合得很好。 玻尔的创造性工作对量子力学的建立有着深远的影响。 让美下元返回退比
上页 下页 返回 退出 根据氢原子的能级及玻尔假设,可以得到氢 原子光谱的波数公式 与氢原子光谱经验公式是一致的。 4 7 2 3 0 1.0973731 10 8 me R h c -1 m = = R 理论值与实验值符合得很好。 玻尔的创造性工作对量子力学的建立有着深远的影响。 4 2 3 2 2 0 1 1 ( ) 8 nk me h c k n = −

四、玻尔理论的缺陷 。玻尔理论仍然以经典理论为基础,定态假设 又和经典理论相抵触。 ●量子化条件的引进没有适当的理论解释。 ·对谱线的强度、宽度、偏振等无法处理。 女意不意适可退此
上页 下页 返回 退出 玻尔理论仍然以经典理论为基础,定态假设 又和经典理论相抵触。 ● ● 量子化条件的引进没有适当的理论解释。 ● 对谱线的强度、宽度、偏振等无法处理。 四、玻尔理论的缺陷

例题13-6在气体放电管中,用能量为12.5eV的电子 通过碰撞使氢原子激发,问受激发的原子向低能级 跃迁时,能发射那些波长的光谱线? 解:设氢原子全部吸收电子的能量后最高能激发 ev,所以 到第个能级,此能级的能量为136 Em-E=13.6- 13.6 n2 把En-E=12.5eV代入上式得 所以 13.6 =12.36,n=3.5取3 13.6-12.5 让美下觉返同速
上页 下页 返回 退出 所以 例题13-6 在气体放电管中,用能量为12.5eV的电子 通过碰撞使氢原子激发,问受激发的原子向低能级 跃迁时,能发射那些波长的光谱线? 解:设氢原子全部吸收电子的能量后最高能激发 1 2 13.6 E E n 13.6 n − = − 2 13.6 12.36 13.6 12.5 n = = − , 把 E E n − = 1 12.5eV 代入上式得 2 13.6 eV n 到第n个能级,此能级的能量为− ,所以 n = 3.5 取3