§13-6不确定关系 电子衍射 观察目镜 1927年海森伯(W.Heisenberg)分析了几个理 想实验后提出了不确定关系。 化贰不元通回退欢
上页 下页 返回 退出 1927年海森伯(W.Heisenberg)分析了几个理 想实验后提出了不确定关系。 §13-6 不确定关系
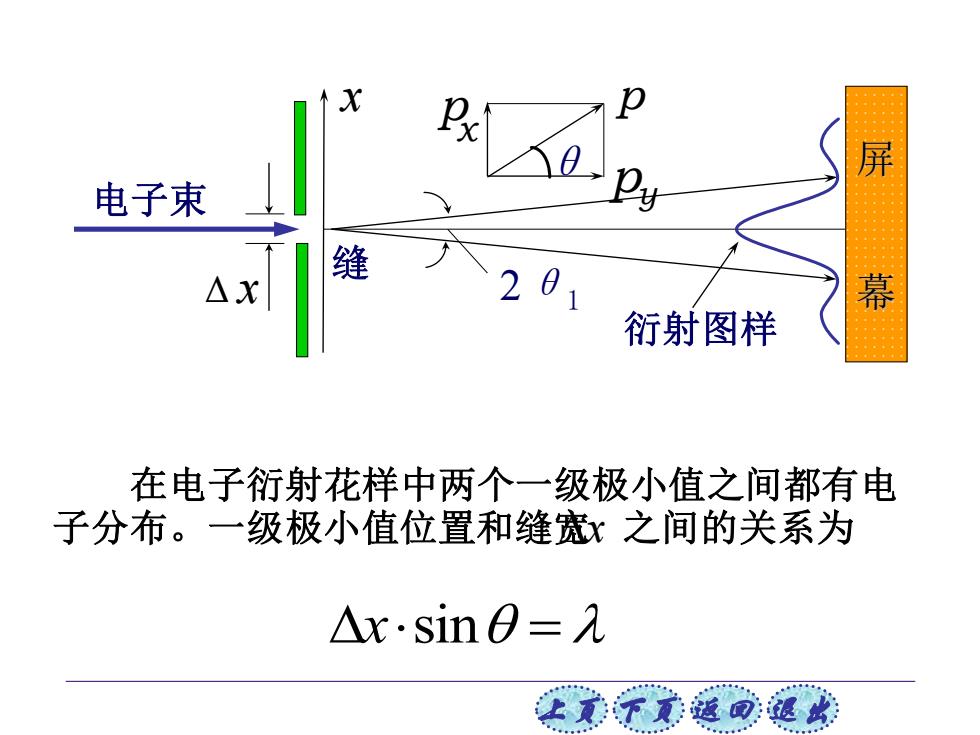
屏 电子束 缝 △X 26 幕 衍射图样 在电子衍射花样中两个一级极小值之间都有电 子分布。一级极小值位置和缝宽x之间的关系为 △x·sin0=λ 让美觉返司退
上页 下页 返回 退出 Δ x 2θ1 电子束 x 缝 屏 幕 衍射图样 p p p x θ y 在电子衍射花样中两个一级极小值之间都有电 子分布。一级极小值位置和缝宽 x 之间的关系为 = x sin

X方向电子的位置不确定量为△x 龙向的分动量△p的不确定量为△P AP:psin= h i h 2△x△x 所以△p·△x=h 考虑到在两个一级极小值之外还有电子出现, 所以有△p·△2h 经严格证明后应改写为: h 2 这就是海森伯坐标和动量的不确定关系式。 让美子意道可退此
上页 下页 返回 退出 所以 这就是海森伯坐标和动量的不确定关系式。 考虑到在两个一级极小值之外还有电子出现, 所以有 经严格证明后应改写为: P p P x θ y 方向的分动量 的不确定量为 x p x x p sin x h h p p x x = = = x 方向电子的位置不确定量为 x x = p x h p x x ≥ h x px ≥ 2 y py ≥ 2 z pz ≥ 2 ,

讨论: .不确定关系式说明用经典物理学量一一动量 、坐标来描写微观粒子行为时将会受到一定的限制 ,因为微观粒子不可能同时具有确定的动量及位置 坐标。 b.不确定关系式可以用来判别对于实物粒子其 行为究竟应该用经典力学来描写还是用量子力学来 描写。 c.对于微观粒子的能量E及它在能态上,停留的 平均时间△t之间也有下面的不确定关系: n △E△t≥ -2 让美下觉返司速此
上页 下页 返回 退出 讨论: a. 不确定关系式说明用经典物理学量——动量 、坐标来描写微观粒子行为时将会受到一定的限制 ,因为微观粒子不可能同时具有确定的动量及位置 坐标。 b. 不确定关系式可以用来判别对于实物粒子其 行为究竟应该用经典力学来描写还是用量子力学来 描写。 c. 对于微观粒子的能量E及它在能态上,停留的 平均时间 t 之间也有下面的不确定关系: E t ≥ 2

原子处于激发态的平均寿命一般为△t≈10-8s 于是激发态能级的宽度为 △E≥ ≈10-8s 2△t 这说明原子光谱有一定宽度,实验已经证实这一点。 上美不家返可退此
上页 下页 返回 退出 这说明原子光谱有一定宽度,实验已经证实这一点。 原子处于激发态的平均寿命一般为 8 t 10 s − 于是激发态能级的宽度为 E ≥ 8 10 s 2 t −

例题13-11设子弹的质量为0.01kg,枪口的直径 为0.5cm,试求子弹射出枪口时的横向速度的不确 定量。 解:枪口直径可以当作子弹射出枪口时位置的 不确定量X。 由于 △px=m△v 根据不确定关系得 五 △V =1.05×10-30m/s 2m△x 和子弹飞行速度每秒几百米相比,这速度的不确 定性是微不足道的,所以子弹的运动速度是确定的。 王文不美菠面:退收
上页 下页 返回 退出 和子弹飞行速度每秒几百米相比,这速度的不确 定性是微不足道的,所以子弹的运动速度是确定的。 例题13-11 设子弹的质量为0.01㎏,枪口的直径 为0.5㎝,试求子弹射出枪口时的横向速度的不确 定量。 根据不确定关系得 解 : 枪口直径可以当作子弹射出枪口时位置的 不确定量 x 。 由于 x x = p m v ≥ x v 30 1.05 10 m / s 2m x − =

例题13-12电视显像管中电子的加速度电压为10kV, 电子枪的枪口的直径为0.01cm.试求电子射出电子枪 后的横向速度的不确定量。 解:电子横向位置的不确定量△x=0.01cm h △Vx2 2m 1.05×1034J·s 2×9.11×10-31kg×1×10-4m =1.05×10-30m/s=0.58m/s 由于△V≤V,所以电子运动速度相对来说仍 然是相当确定的,波动性不起什么实际影响
上页 下页 返回 退出 例题13-12 电视显像管中电子的加速度电压为10 kV, 电子枪的枪口的直径为0.01 ㎝. 试求电子射出电子枪 后的横向速度的不确定量。 解:电子横向位置的不确定量 =x 0.01cm 34 31 4 1.05 10 2 9.11 10 1 10 J s kg m − − − = 30 1.05 10 0.58 m s m s − = = x v ≥ 2m x 由于 ,所以电子运动速度相对来说仍 然是相当确定的,波动性不起什么实际影响。 ≤ x v v

例题13-13试求原子中电子速度的不确定量,取原子 的线度约为10-10m。 解:原子中电子位置的不确定量r≈1010m, 由不确定关系式得 h 1.05×10-34Js △V2 2x9.1x10-kg×10-m 5.8×105m/s 2m△x 由玻尔理论可估算出氢原子中电子的轨道运动速 度约为10°m/s,可见速度的不确定量与速度大小的数 量级基本相同.因此原子中电子在任一时刻没有完全 确定的位置和速度,也没有确定的轨道,不能看成经典 粒子,波动性十分显著。 王文下美菠面:退收
上页 下页 返回 退出 例题13-13 试求原子中电子速度的不确定量, 取原子 的线度约为 10-10 m。 由不确定关系式得 解: 原子中电子位置的不确定量 10 r 10 , m − 由玻尔理论可估算出氢原子中电子的轨道运动速 度约为 ,可见速度的不确定量与速度大小的数 量级基本相同.因此原子中电子在任一时刻没有完全 确定的位置和速度,也没有确定的轨道,不能看成经典 粒子,波动性十分显著。 6 10 m s 34 5 31 10 1.05 10 J s 5.8 10 m s 2 9.11 10 kg 10 m − − − = = x v ≥ 2m x

例题13-14实验测定原子核线度的数量级为10-14m, 试应用不确定度关系来估算电子如被束缚在原子核中的 动能,从而判断原子核是由质子和电子组成是否可能。 解:取电子在原子核中位置的不确定量△r≈104m 由不确定关系得 △p≥ =0.53×1020kgm/s 2△r 由于动量的数值不可能小于它不确定量,故电子的动量 p20.53×10-20kgm/s 让意子家通回退此
上页 下页 返回 退出 由于动量的数值不可能小于它不确定量,故电子的动量 由不确定关系得 例题13-14 实验测定原子核线度的数量级为10-14m, 动能,从而判断原子核是由质子和电子组成是否可能。 试应用不确定度关系来估算电子如被束缚在原子核中的 解:取电子在原子核中位置的不确定量 14 r 10 m − 20 0.53 10 kg m s − p ≥ = 2r 20 0.53 10 kg m s − p≥

考虑到电子在此动量下有极高的速度,需要 应用相对论的能量动量公式 E2=p'c2+mic 故 E=Vp2c2+mc≈1.6x102J 电子在原子核中的动能 Es=E-m,c2≈1.6×10-12J 理论证明,电子具有这样大的动能足以把原子核 击碎,所以,把电子禁锢在原子核内是不可能的,这 就否定了原子核是由质子和电子组成的假设。 让美子元返司退
上页 下页 返回 退出 理论证明,电子具有这样大的动能足以把原子核 击碎,所以,把电子禁锢在原子核内是不可能的,这 就否定了原子核是由质子和电子组成的假设。 电子在原子核中的动能 故 考虑到电子在此动量下有极高的速度,需要 应用相对论的能量动量公式 2 2 2 2 4 E p c m c = + 0 2 2 2 4 12 0 E p c m c 1.6 10 J − = + 2 12 0 E E m c 1.6 10− k = − J