
§13-8一维定态薛定谔方程的应用 一、一维无限深势阱 若质量为m的粒子,在保守力场的作用下,被限 制在一定的范围内运动,其势函数称为势阱。 为了简化计算,提出理想模型一一无限深势阱。 一 维无限深势阱: 00 U(x)1 U(x)= 0<x<a x≤0,x2a L 王觉下元菠面:退收
上页 下页 返回 退出 若质量为m的粒子,在保守力场的作用下,被限 制在一定的范围内运动,其势函数称为势阱。 为了简化计算,提出理想模型——无限深势阱。 一维无限深势阱: §13-8 一维定态薛定谔方程的应用 一、一维无限深势阱 a x o U x( ) = 0 U(x) 0 x a x≤0,x≥a
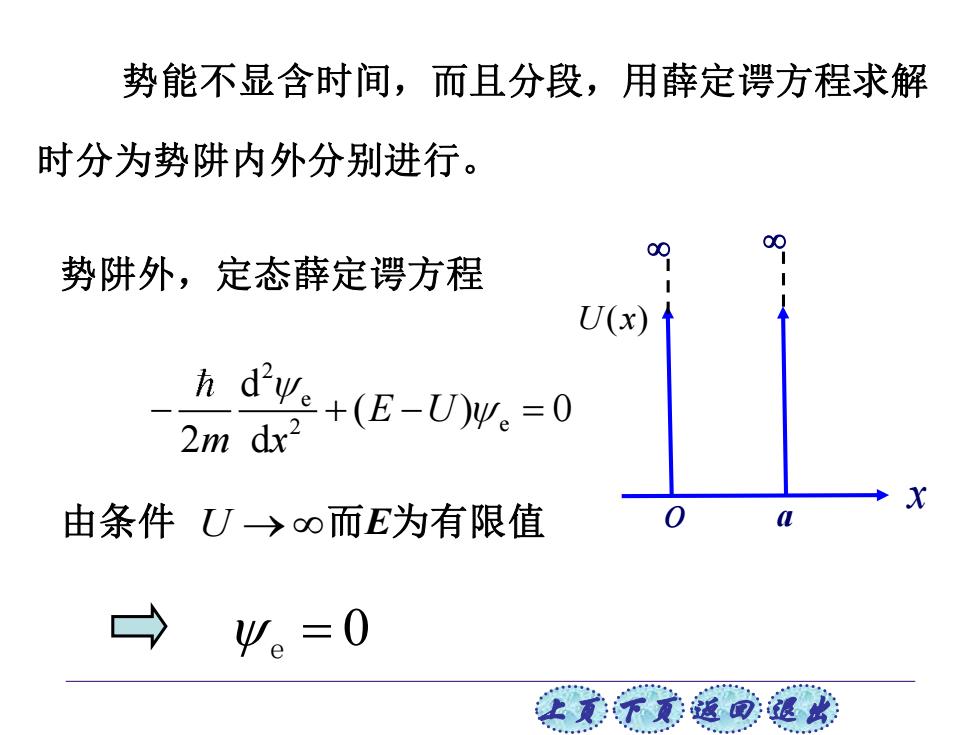
势能不显含时间,而且分段,用薛定谔方程求解 时分为势阱内外分别进行。 势阱外,定态薛定谔方程 U(x)1 九d+(E-U)m.=0 2m dx2 由条件UJ→∞而E为有限值 Ψ。=0 上意不家道可退欢
上页 下页 返回 退出 势能不显含时间,而且分段,用薛定谔方程求解 时分为势阱内外分别进行。 势阱外,定态薛定谔方程 2 e 2 e d ( ) 0 2 d E U m x − + − = 由条件 U → 而E为有限值 = 0 e a x o U x( )

保守力与势能之间的关系:F=- dU(x) dx 在势阱边界处,粒子要受到无限大、指向阱内的 力,表明粒子不能越出势阱,即粒子在势阱外的概率 为0。 势阱内的一维定态薛定谔方程为 h d'w=EW 2m dx2 k2=2m6 h2 解为 w(x)=Csin(ka+δ) 让美觉返司退
上页 下页 返回 退出 保守力与势能之间的关系: 在势阱边界处,粒子要受到无限大、指向阱内的 力,表明粒子不能越出势阱,即粒子在势阱外的概率 为0。 势阱内的一维定态薛定谔方程为 解为 2 2 i 2 i d 2 d E m x − = 2 2 2mE k = i ( ) sin( ) x C kx = + d ( ) d U x F x = −

由边界条件得 W;(0)=Csin=0 w;(a)=Csin ka=0 δ=0 ka=nm,n=1,2,3,. 据归一化条件,得 cmd →c月 2 得波函数表达式:必(x,t)= S1nxe序 a
上页 下页 返回 退出 由边界条件得 据归一化条件,得 得波函数表达式: i i (0) sin 0 ( ) sin 0 C a C ka = = = = 0 ka n n, 1, 2,3, = = = π 2 2 0 0 ( , ) d sin d 1 a a n x x t x C x a = = π 2 C a = 2 ( , ) sin n Et x t x a a − = i i π e

Ψe(x,t)=0 波函数 E ↑E n=4 E4=16E 讨论: (1)粒子能量不能取连续值 n=3 E3=9E 由 k2=2mE ,k= nn n=2 E2=4E 方2 n=l a h2k2n2π2h2 得 E= =Enn=1,2,3,. 2m 2ma2 能量取分立值(能级),能量量子化是 粒子处于束缚态的所具有的性质。 让美觉返司退
上页 下页 返回 退出 (1)粒子能量不能取连续值 得 能量取分立值(能级),能量量子化是 粒子处于束缚态的所具有的性质。 由 讨 论: 波函数 ( , ) 0 2 ( , ) sin Et x t n x t x a a e i i π e − = = 2 2 2 2 2 2 1 2 3 2 2 n k n E E n m ma = = = = , π 2 2 2mE n k k a = = , π E1 n =1 2 1 n = 2 E E = 4 3 1 n = 3 E E = 9 4 1 n = 4 E E =16 O a E

(2)粒子的最小能量不等于零 最小能量E= n2h2 2ma 也称为基态能或零点能。 零点能的存在与不确定度关系协调一致。 上美不家返可退此
上页 下页 返回 退出 (2)粒子的最小能量不等于零 最小能量 也称为基态能或零点能。 零点能的存在与不确定度关系协调一致。 2 2 1 2 2 n E ma =
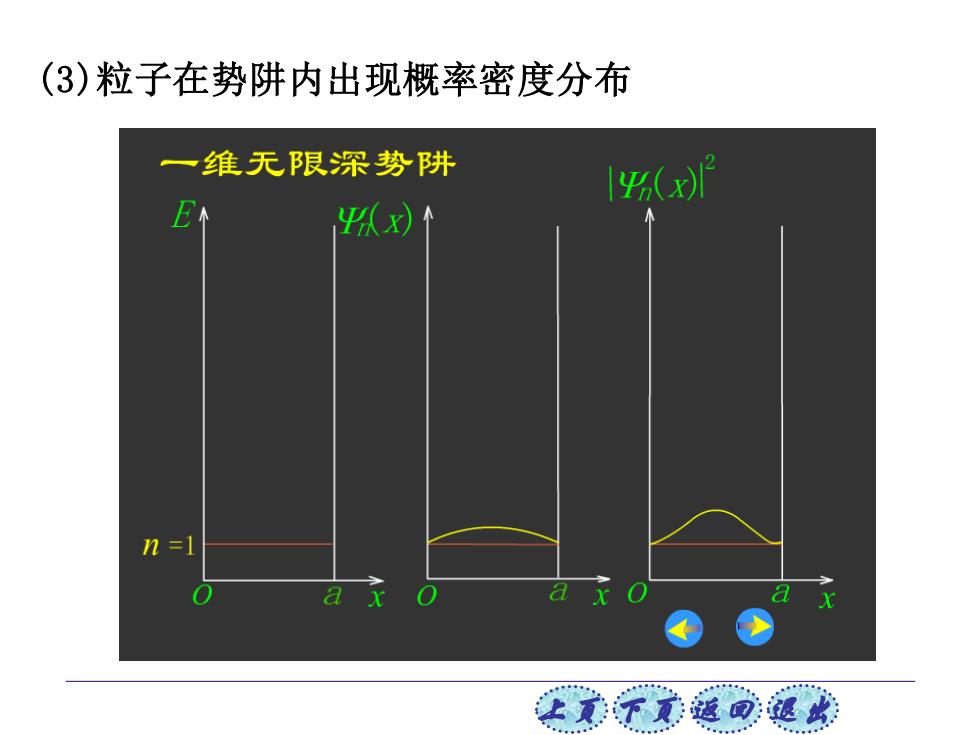
(3)粒子在势阱内出现概率密度分布 一维无限深势阱 x E 队个 n=1 让美下觉返司速此
上页 下页 返回 退出 (3)粒子在势阱内出现概率密度分布
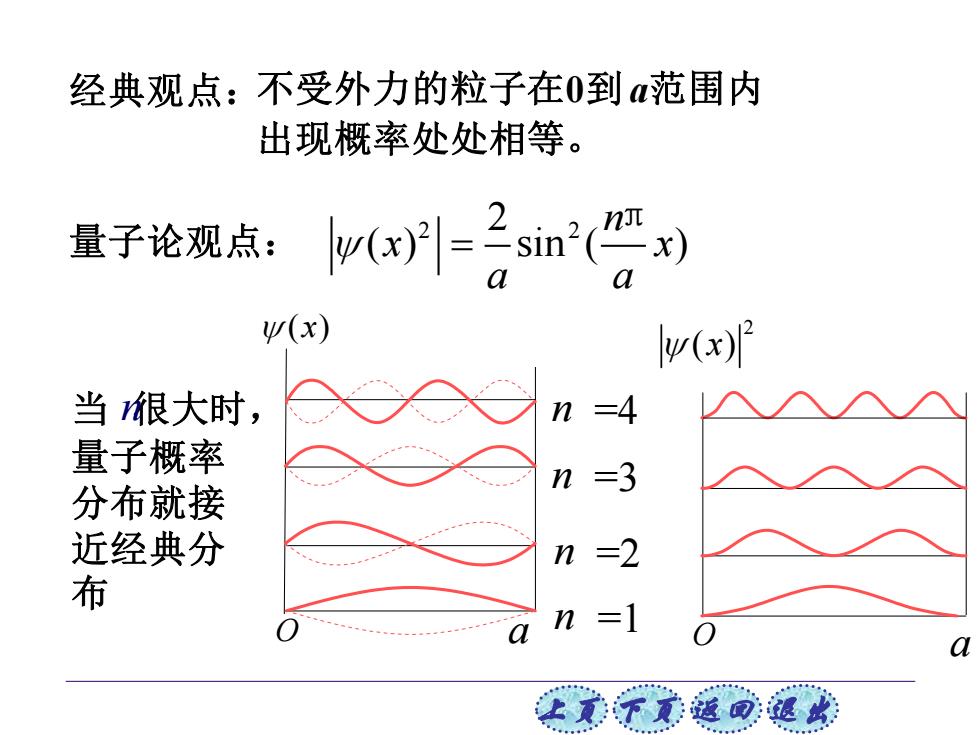
经典观点:不受外力的粒子在0到范围内 出现概率处处相等。 量子论观点: 2sin') w(x) (x) 当很大时, n =4 量子概率 n =3 分布就接 近经典分 n =2 布 n =1 a 上意子意返回退此
上页 下页 返回 退出 不受外力的粒子在0到a范围内 出现概率处处相等。 量子论观点: 经典观点: 2 2 2 ( ) sin ( ) n x x a a = π a O a =1 =2 =3 n =4 n n n O 当 很大时, 量子概率 分布就接 近经典分 布 n ( ) x 2 ( ) x
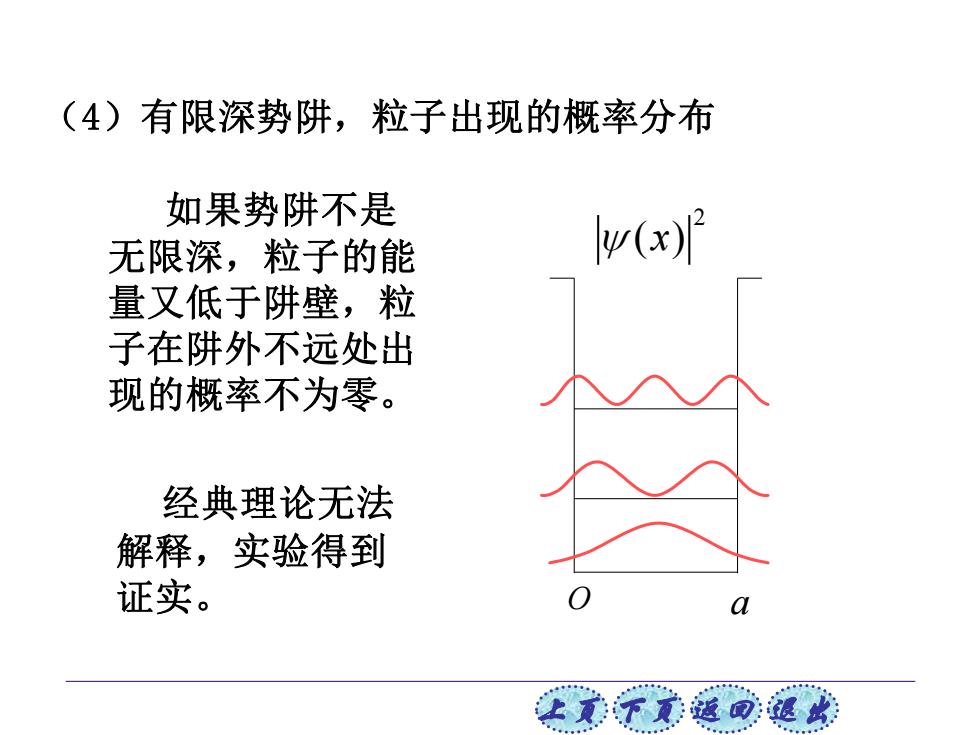
(4)有限深势阱,粒子出现的概率分布 如果势阱不是 无限深,粒子的能 w(x) 量又低于阱壁,粒 子在阱外不远处出 现的概率不为零。 经典理论无法 解释,实验得到 证实。 让美下觉返同速
上页 下页 返回 退出 (4)有限深势阱,粒子出现的概率分布 如果势阱不是 无限深,粒子的能 量又低于阱壁,粒 子在阱外不远处出 现的概率不为零。 经典理论无法 解释,实验得到 证实。 O a 2 ( ) x

例题13-16设想一电子在无限深势阱,如果势阱宽度 分别为1.0×10-2m和10-10m。试讨论这两中情况下相 邻能级的能量差。 解:根据势阱中的能量公式 E= 2h22- h2 n 2ma 8ma? 得到两相邻能级的能量差 AE=En1-En=(2n+l) 8a2 可见两相邻能级间的距离随着量子数的增加而增 加,而且与粒子的质量m和势阱的宽度a有关
上页 下页 返回 退出 得到两相邻能级的能量差 例题 13-16 设想一电子在无限深势阱,如果势阱宽度 分别为1.0×10-2m和10-10m 。试讨论这两中情况下相 邻能级的能量差。 解:根据势阱中的能量公式 可见两相邻能级间的距离随着量子数的增加而增 加,而且与粒子的质量m和势阱的宽度a有关。 2 2 2 2 2 2 2 2 8 h E n n ma ma = = π 2 1 2 (2 1) 8 n n h E E E n ma = − = + +