§13-9量子力学中的氢原子问题 一、氢原子的薛定谔方程 氢原子中电子的势能函数U= 4T8o' 定态薛定谔方程 方2 ew-o 4π6 r=vx2+y2+z 电 为使求解的问题变得简便, 原核子 通常采用球坐标(r,0,) X
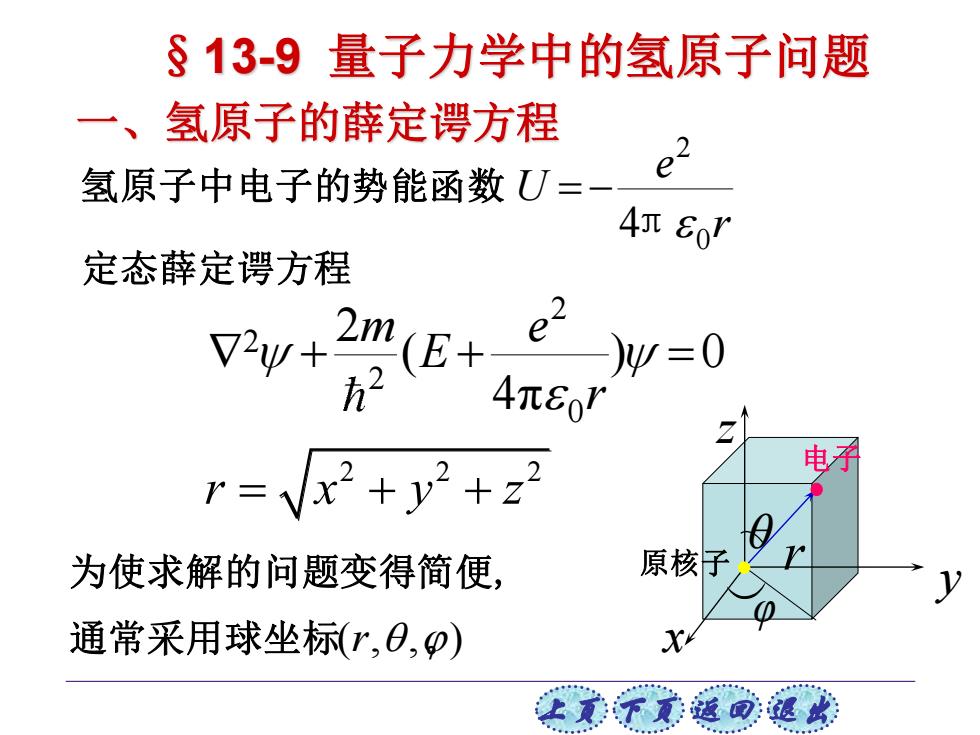
上页 下页 返回 退出 氢原子中电子的势能函数 定态薛定谔方程 x y z θ φ r 电子 原核子 一、氢原子的薛定谔方程 2 0 4 e U r = − π 2 2 2 0 2 ( ) 0 4π m e E r + + = 2 2 2 r x y z = + + 为使求解的问题变得简便, 通常采用球坐标( , , ) r 。 §13-9 量子力学中的氢原子问题

拉普拉斯算符变为 1 1 8w r2 Or (sin ∂0 r2 sin2 e do 设波函数为w(r,B,p)=R(r)⊙(0)Φ(p) 代入薛定谔方程,采用分离变量法得到三个常 微分方程。 在解波函数时,考虑到波函数应满足的标准 条件,很自然地得到氢原子的量子化特征。 王觉下元菠面:退收
上页 下页 返回 退出 拉普拉斯算符变为 设波函数为 代入薛定谔方程,采用分离变量法得到三个常 微分方程。 在解波函数时,考虑到波函数应满足的标准 条件,很自然地得到氢原子的量子化特征。 2 2 2 2 2 2 2 2 1 1 1 ( ) (sin ) sin sin r r r r r r = + + ( , , ) ( ) ( ) ( ) r R r =

三个函数分别满足关系 d2Φ do +mΦ=0 1 d sin@do
上页 下页 返回 退出 三个函数分别满足关系 2 2 2 0 ml + = d d 2 2 1 sin 0 sin sin ml + − = d d d d 2 2 2 2 2 0 1 2 0 4 R m e r E R r r r r r + + − = d d d d π

二、量子化条件和量子数 1.能量量子化和量子数 在求解R(r)得到氢原子能量必须满足量子化条件为 me4 1 32m2e2h2n2 8e,2h2n2 -13.61 n称为主量子数 同玻尔得到的氢原子的能量公式一致,但却没有认 为的假设。 让美下觉返同速
上页 下页 返回 退出 同玻尔得到的氢原子的能量公式一致,但却没有认 为的假设。 n 称为主量子数 二、量子化条件和量子数 1.能量量子化和量子数 在求解 R r( ) 得到氢原子能量必须满足量子化条件为 4 4 2 2 2 2 2 2 2 2 0 0 1 1 1 13.6 32 8 n me me E n h n n = − = − = − π
n=1基态能量E,=-13.6eV E 5 n=2,3,.对应的能量称为激发态能量 4 E,=-3.40eVE3=-1.51eV E 3 当n很大时,能级间隔消失而变为连续。 E21 2 当n=o,E=0 几=0对应于电子被电离,氢原子 的电子电离能为 E-E=13.6eV 上意不意道可退欢
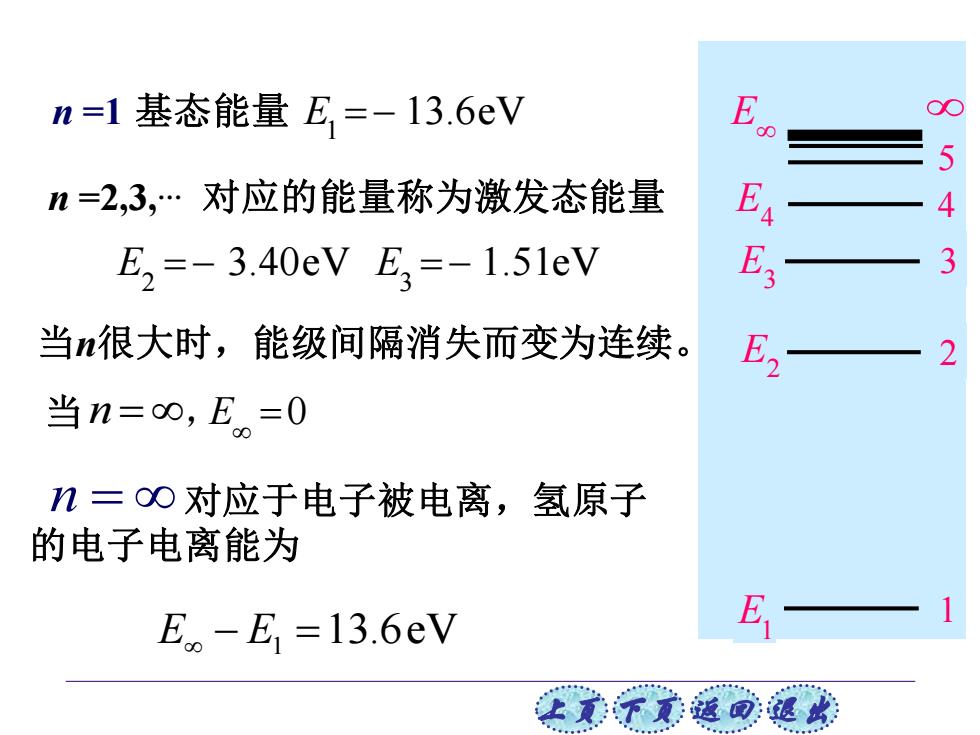
上页 下页 返回 退出 n =2,3,. 对应的能量称为激发态能量 当n很大时,能级间隔消失而变为连续。 对应于电子被电离,氢原子 的电子电离能为 n = 1 1 E 2 3 2 E 3 E 4 5 4 E n =1 基态能量 E 1 E = − 13.6eV 2 3 E E = − = − 3.40eV 1.51eV 当 , E 0 n = = 1 E E − =13.6eV

2.轨道角动量量子化和角量子数 在求解角量为胶量的函数所满足的方程时,进 一步得到角动量量子化的结果。 L=V10+1)克1=1,2,3,.,(n-1) 1称为角量子数,或副量子数。 说明角动量只能取由决定的一系列分立值, 即角动量也是量子化的。 处于能级的原子,其角动量共有n种可能值 ,即1=0,1,2,用sp54,.表示角动量状态。 让美下觉返同速
上页 下页 返回 退出 说明角动量只能取由l决定的一系列分立值, 即角动量也是量子化的。 2.轨道角动量量子化和角量子数 在求解角量 为变量的函数所满足的方程时,进 一步得到角动量量子化的结果。 , l 称为角量子数,或副量子数。 L l l = + ( 1) , l n = − 1,2,3, ,( 1) 处于能级 的原子,其角动量共有n种可能值 ,即 ,用s, p, d,.表示角动量状态。 E n l n = − 0 1 2 1 ,
氢原子内电子的状态 1=0 1=1 1=2 1=3 1=4 1=5 (s) (p) (d) (f) (g) (h) n=1 1s n=2 2s 2p n=3 3s 3p 3d n=4 4s 4p 4d 4f n=5 5s 5p 5d 5f 5g n=6 6s 6p 6d 6f 6g 6h 让意不意示通命运
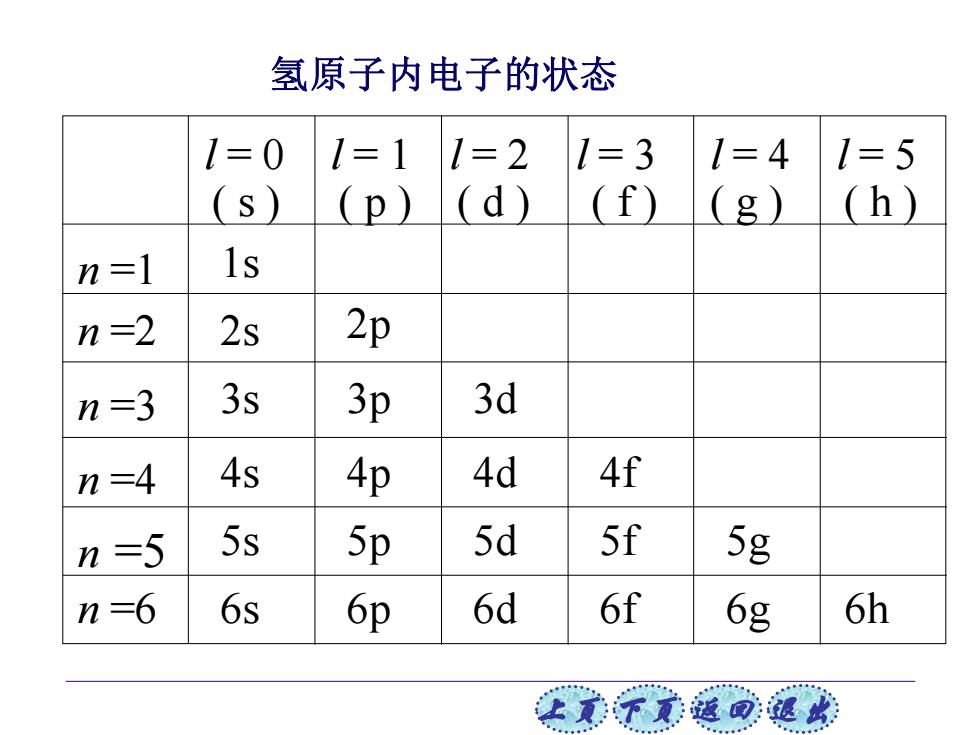
上页 下页 返回 退出 氢原子内电子的状态 n =1 n =2 n =3 n =4 n =5 n =6 l = 0 l = 1 l = 2 l = 3 l = 4 l = 5 ( s ) ( p ) ( d ) ( f ) ( g ) ( h ) 1s 5s 5p 5d 5f 6s 6p 6d 6f 6g 6h 4s 3s 3p 4f 3d 4p 4d 5g 2s 2p

3.轨道角动量空间量子化和磁量子数 氢原子中电子绕核运动的角动量不仅大小取分离 值,其方向也有一定限制。若取外磁场的方向为 轴,z角动量在轴的投影只能取 L.=m,hm,=0,±1,+2,±l m,称为磁量子数。对于一定的角量子数l,m, 可以取2(1+1)个值。 让美下觉返司速此
上页 下页 返回 退出 3.轨道角动量空间量子化和磁量子数 称为磁量子数。对于一定的角量子数 可以取 个值。 ml l l m , 2(l +1) L m z l = 0, 1, 2,., m l l = 氢原子中电子绕核运动的角动量不仅大小取分离 值,其方向也有一定限制。若取外磁场B的方向为 轴,角动量在 轴上的投影 z 只能取 Lz z
B( 2h 角动量的空间量子化 L=√6h 2h 1'=2 让意不家返可退此
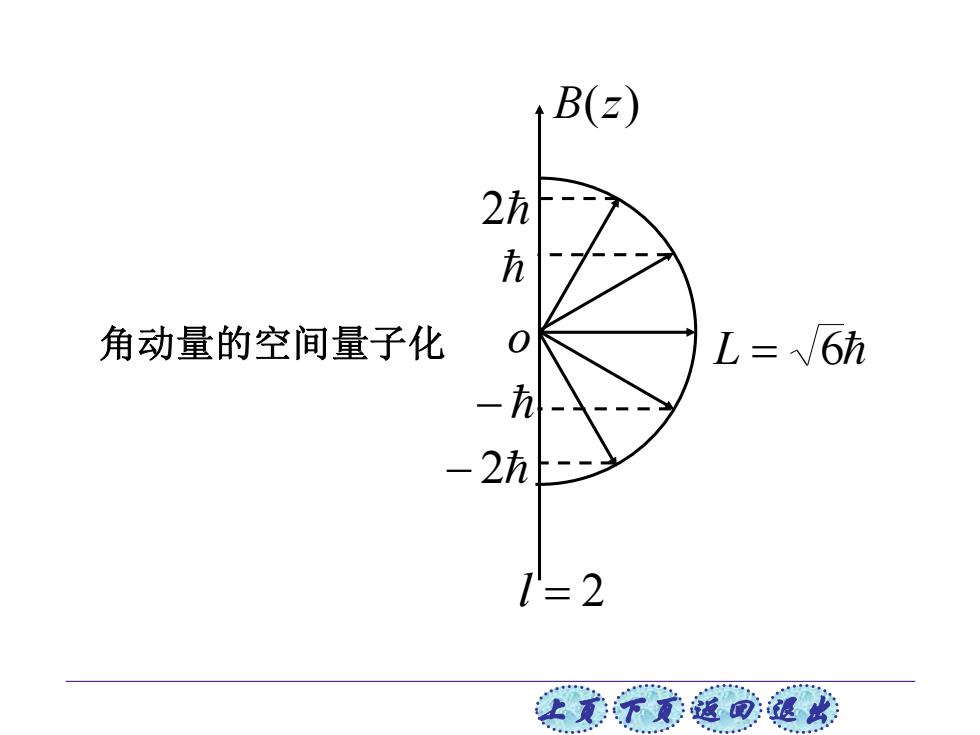
上页 下页 返回 退出 B(z) o 2 − − 2 L = 6 l = 2 角动量的空间量子化
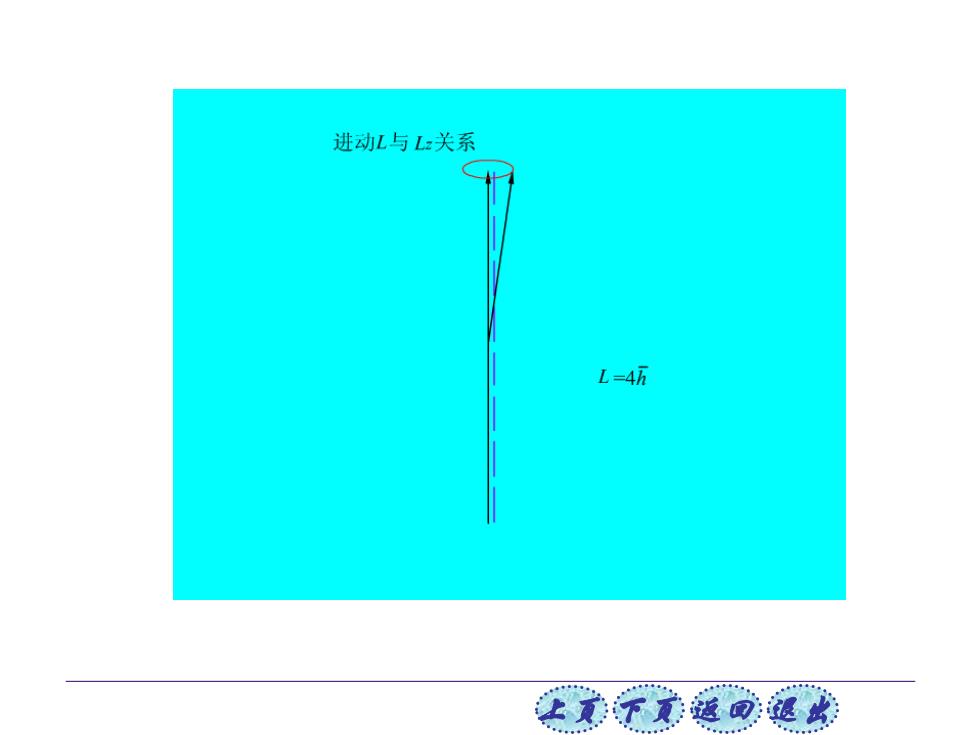
进动L与Lz关系 L=4五 让美觉返司退
上页 下页 返回 退出