
第12章气体动理论 扫描隧道显微镜(STM)
第12章 气体动理论 扫描隧道显微镜(STM)
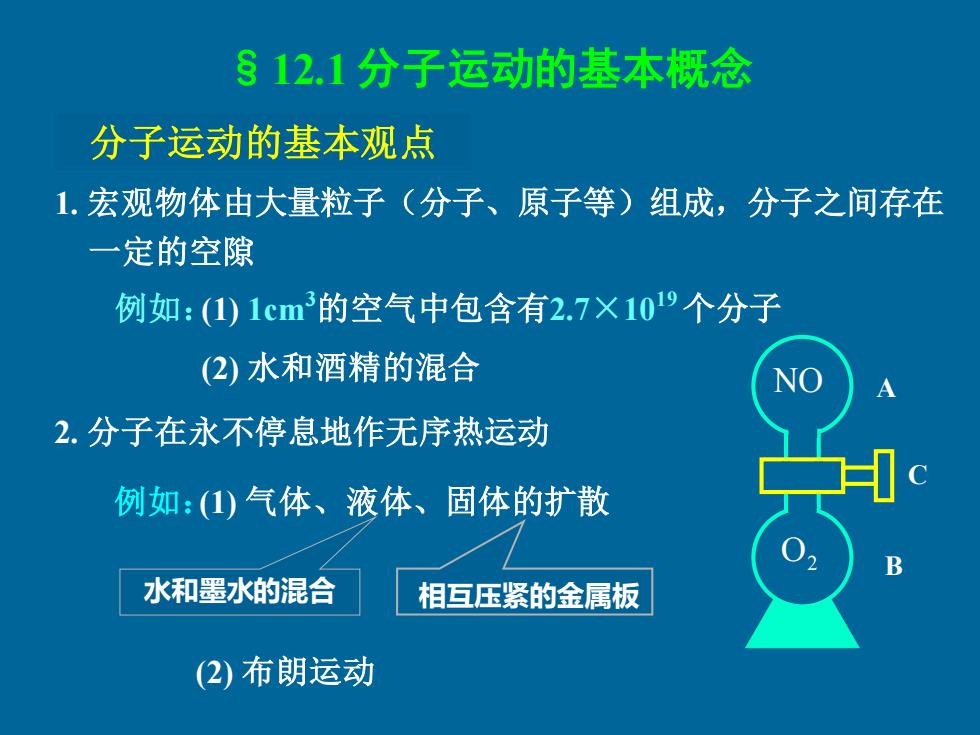
§12.1分子运动的基本概念 分子运动的基本观点 1.宏观物体由大量粒子(分子、原子等)组成,分子之间存在 一定的空隙 例如:(1)1cm3的空气中包含有2.7×109个分子 (2)水和酒精的混合 2.分子在永不停息地作无序热运动 例如:(1)气体、液体、固体的扩散 水和墨水的混合 相互压紧的金属板 (2)布朗运动
§12.1 分子运动的基本概念 分子运动的基本观点 1. 宏观物体由大量粒子(分子、原子等)组成,分子之间存在 一定的空隙 2. 分子在永不停息地作无序热运动 (1) 气体、液体、固体的扩散 水和墨水的混合 相互压紧的金属板 例如:(1) 1cm3的空气中包含有2.7×1019 个分子 (2) 水和酒精的混合 例如: (2) 布朗运动 NOO2 A B C

布朗运动 3.分子间存在相互作用力 假定分子间的相互作用力有球对称性时,分子间的相互作 用(分子力可近似地表示为 (s>t)
3. 分子间存在相互作用力 假定分子间的相互作用力有球对称性时,分子间的相互作 用(分子力)可近似地表示为 ( 布 朗 运 动 ) (s t) r r f s t = −
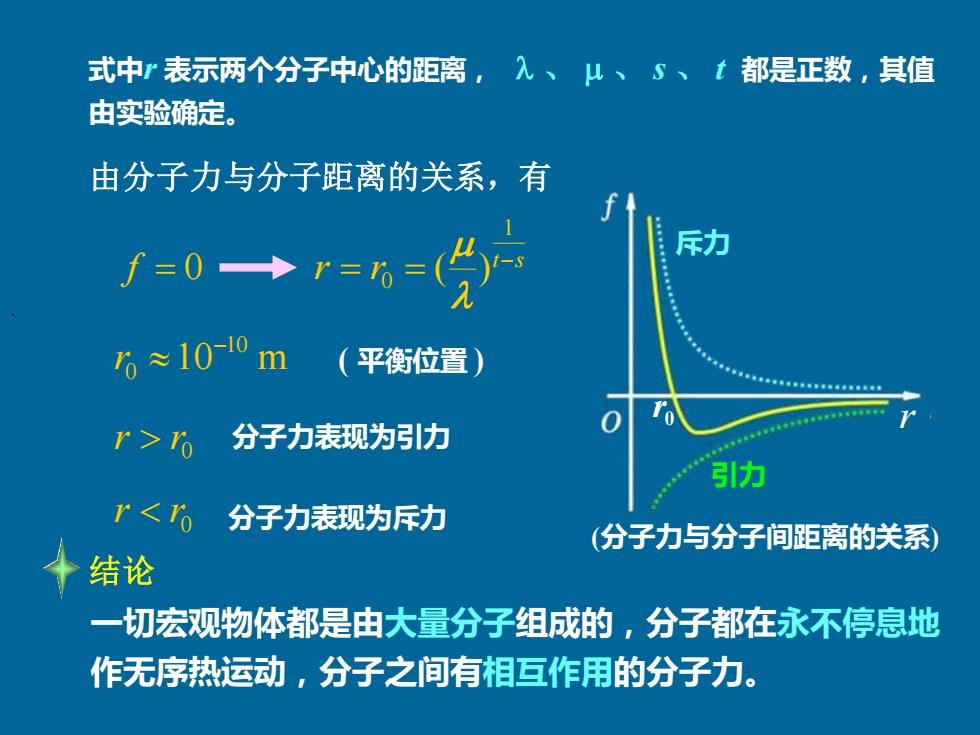
式中r表示两个分子中心的距离,入、山、S、t都是正数,其值 由实验确定。 由分子力与分子距离的关系,有 斥力 f=0r=%= 6≈10-10m (平衡位置) r>ro 分子力表现为引力 引力 r≤% 分子力表现为斥力 (分子力与分子间距离的关系) 十结论 一切宏观物体都是由大量分子组成的,分子都在永不停息地 作无序热运动,分子之间有相互作用的分子力
、 式中r 表示两个分子中心的距离, 、 、 s 、 t 都是正数,其值 由实验确定。 0 r 斥力 引力 r (分子力与分子间距离的关系) t s r r − = = 1 0 ( ) f = 0 0 r r 0 r r 分子力表现为斥力 分子力表现为引力 由分子力与分子距离的关系,有 10 m 10 0 − r ( 平衡位置 ) 一切宏观物体都是由大量分子组成的,分子都在永不停息地 作无序热运动,分子之间有相互作用的分子力。 结论

§12:2气体分子的热运动 气体分子运动的规律 1.气体分子热运动可以看作是在惯性支配下的自由运动 (1)由于气体分子间距离很大,而分子力的作用范围又很小, 除分子与分子、分子与器壁相互碰撞的瞬间外,气体分 子间相互作用的分子力是极其微小的。 (2)由于气体分子质量一般很小,因此重力对其作用一般可 以忽略。 2.气体分子间的相互碰撞是非常频繁的 一秒内一个分子和其它分子大约要碰撞几十亿次(10次/秒》
§12.2 气体分子的热运动 气体分子运动的规律 1. 气体分子热运动可以看作是在惯性支配下的自由运动 (1) 由于气体分子间距离很大,而分子力的作用范围又很小, 除分子与分子、分子与器壁相互碰撞的瞬间外,气体分 子间相互作用的分子力是极其微小的。 (2) 由于气体分子质量一般很小,因此重力对其作用一般可 以忽略。 2. 气体分子间的相互碰撞是非常频繁的 一秒内一个分子和其它分子大约要碰撞几十亿次(109次/秒)

3.气体分子热运动服从统计规律 ·统计的方法 物理量M的统计平均值 ☑=N4M,+NgM2+. N N=N4+Ng+. N是M的测量值为M的次数,实验总次数为N M=lim(N M+NgMg+)/N 状态A出现的概率 W=im(N/N) N->oo 归一化条件 ∑W,=1
3. 气体分子热运动服从统计规律 统计的方法 物理量M 的统计平均值 N N M N M M A A + B B + = M NAMA NBMB N N = lim( + +) → 状态A出现的概率 W lim(N N ) A N A → = 归一化条件 =1 i Wi · Ni 是M 的测量值为 Mi 的次数,实验总次数为N = + + N NA NB
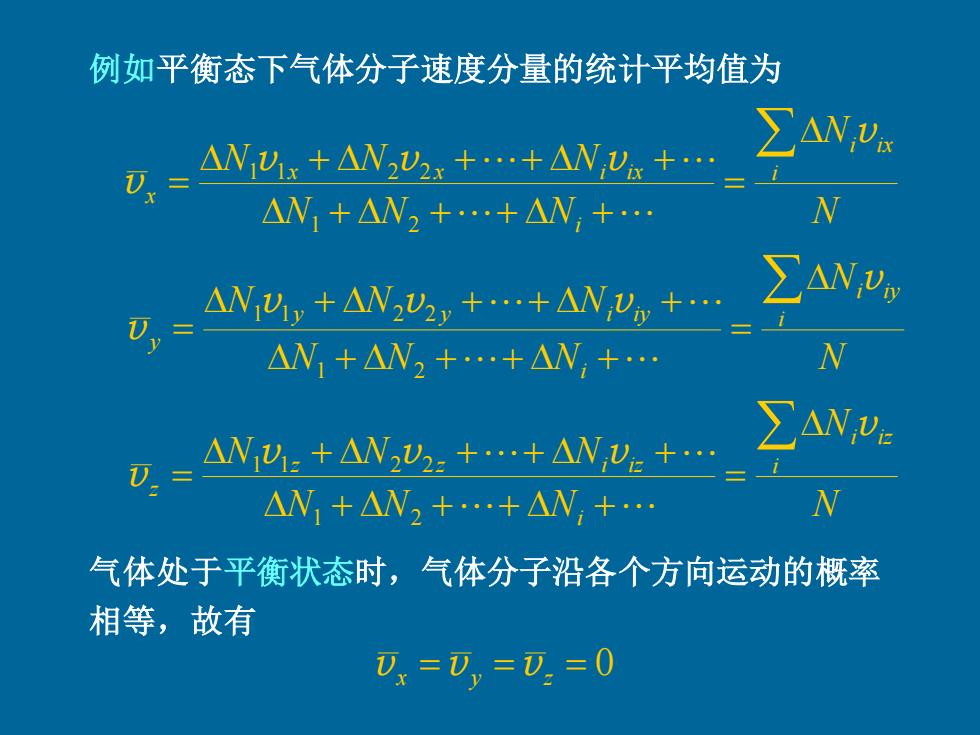
例如平衡态下气体分子速度分量的统计平均值为 ANyk+AN2V2x+.+△WV+ ∑AWua △N+△N2+.+△N,+. N N,+AV,业,+.+AWn+. ∑ANV △W1+△N2++AN,+. N △Vy:+NV2:++W,V2+ ∑AWve △W1+△N2+.+△N,+ N 气体处于平衡状态时,气体分子沿各个方向运动的概率 相等,故有 U=亚,y==0
例如平衡态下气体分子速度分量的统计平均值为 N N N N N N N N i i ix i x x i ix x = + + + + + + + + = v v v v v 1 2 1 1 2 2 N N N N N N N N i i iy i y y i iy y = + + + + + + + + = v v v v v 1 2 1 1 2 2 N N N N N N N N i i iz i z z i iz z = + + + + + + + + = v v v v v 1 2 1 1 2 2 气体处于平衡状态时,气体分子沿各个方向运动的概率 相等,故有 = = = 0 vx vy vz

又如平衡态下气体分子速度分量平方的统计平均值为 ∑ANU∑N&∑NG∑AN, N N =+v+ 由于气体处于平衡状态时,气体分子沿各个方向运动的概 率相等,故有 =U= ===元
N N i i i 2 2 v v = 2 2 2 vx =vy =vz 2 2 2 =vx +vy +vz 2 2 2 2 3 1 vx =vy =vz = v 由于气体处于平衡状态时,气体分子沿各个方向运动的概 率相等,故有 N N N N N N iz i iy i i ix i i i 2 2 2 v v v + + = 又如平衡态下气体分子速度分量平方的统计平均值为
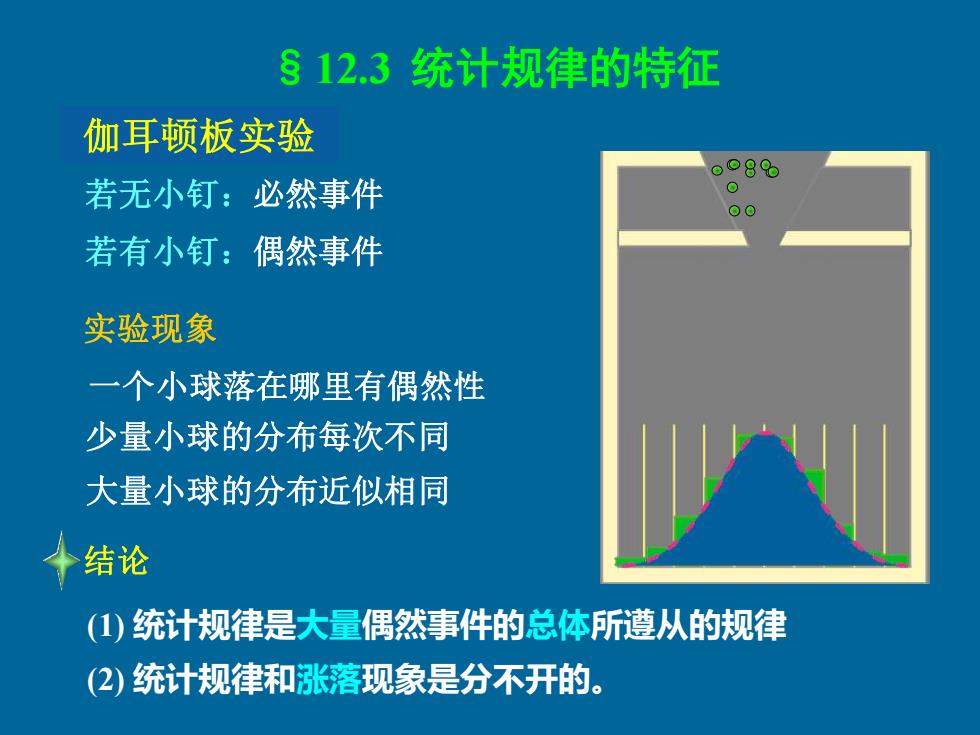
§12.3统计规律的特征 伽耳顿板实验 o86 若无小钉:必然事件 00 若有小钉:偶然事件 实验现象 一个小球落在哪里有偶然性 少量小球的分布每次不同 大量小球的分布近似相同 个结论 (1)统计规律是大量偶然事件的总体所遵从的规律 (2)统计规律和涨落现象是分不开的
§12.3 统计规律的特征 伽耳顿板实验 若无小钉:必然事件 若有小钉:偶然事件 一个小球落在哪里有偶然性 实验现象 少量小球的分布每次不同 大量小球的分布近似相同 (1) 统计规律是大量偶然事件的总体所遵从的规律 (2) 统计规律和涨落现象是分不开的。 结论

§12.4理想气体的压强公式 一,理想气体的微观模型 ()不考虑分子的内部结构并忽略其大小 (2)分子力的作用距离很短,可以认为气体分子之间除了 碰撞的一瞬间外,其相互作用力可忽略不计。 (③)碰撞为完全弹性 理想气体分子好像是一个个没有大小并且除碰撞瞬间外没 有相互作用的弹性球。 二.平衡态气体分子的统计性假设 1.每个分子的运动速度各不相同,且通过碰撞不断发生变化
§12.4 理想气体的压强公式 一. 理想气体的微观模型 (1) 不考虑分子的内部结构并忽略其大小 (2) 分子力的作用距离很短,可以认为气体分子之间除了 碰撞的一瞬间外,其相互作用力可忽略不计。 (3) 碰撞为完全弹性 理想气体分子好像是一个个没有大小并且除碰撞瞬间外没 有相互作用的弹性球。 二. 平衡态气体分子的统计性假设 1. 每个分子的运动速度各不相同,且通过碰撞不断发生变化