广东工业大学：《大学物理》课程教学课件（PPT讲稿）第十四章 波动光学基础（14.1-14.8）

第14拿波动光学基础 北极光

第14章 波动光学基础 北极光

§14. 1光是电磁波 一.电磁波 1.电磁波的产生 凡做加速运动的电荷都是电磁波的波源 例如：天线中的振荡电流 分子或原子中电荷的振动 2.对电磁波(E,)的描述（平面简谐波） E-E,cos) H=Hcos@(t-） ●平面简谐电磁波的性质 ()它和产传播速度相同、 相位相同 (②)电磁波是横波E×户∥元

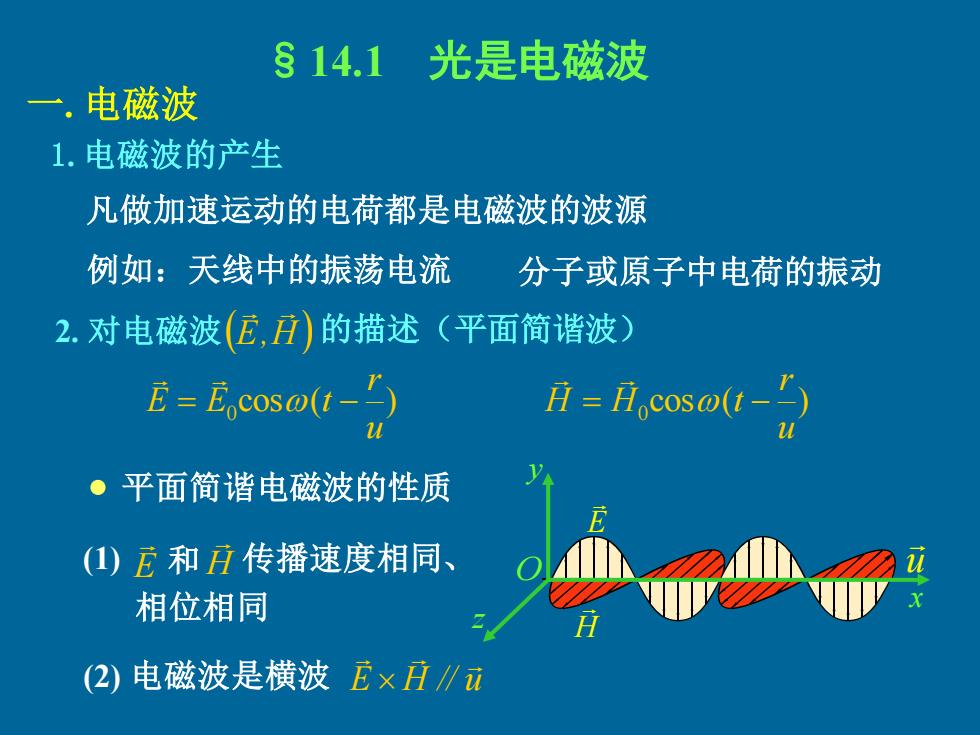
§14.1 光是电磁波 一. 电磁波 u  E  H  1. 电磁波的产生 凡做加速运动的电荷都是电磁波的波源 例如：天线中的振荡电流 分子或原子中电荷的振动 2. 对电磁波 cos ( ) 0 u r E = E  t −   cos ( ) 0 u r H = H  t −   平面简谐电磁波的性质 (1) (2) 电磁波是横波 • (E,H ) 的描述（平面简谐波）   E  H  和 传播速度相同、 相位相同 E H // u     O x y z

3)量值上 √eE=uH (4④)波速 真空中C= =2.9979×10ms e046 (⑤)电磁波具有波的共性 在介质分界面处有反射和折射 C Eu 折射率n= E,4,≈√E, N800 3.电磁波的能量密度 1W三 E2 M H2

(3) 量值上 E = H (4) 波速  1 u = 8 1 0 0 2 9979 10 m s 1 − c = = .     (5) 电磁波具有波的共性——在介质分界面处有反射和折射 u c n = 00   = rr =  r   2 2 1 w =  E 3. 电磁波的能量密度 真空中 折射率 2 2 1 +  H

能流密度忑（坡印亭矢量） S=d4.udt.w dA.dt E=√u S8E+,4/32 EH d 8 坡印亭矢量 5=E×月 udt 波的强度I 结论：I正比于E,或H3,通常用其相对强度1=。盼表示

能流密度 dA u  S  uw A t A u t w S =    = d d d d    1 ) 2 1 ( 2 1 2 2 = E + H E = H = EH S E H    =  波的强度 I  + = = = t T t S t T I S S d 1  + = − t T t t u r E H t T cos ( )d 1 2 0 0  2 0 2 1 E   = 结论：I 正比于 E0 2 或 H0 2 , 通常用其相对强度 2 0 2 1 I = E 坡印亭矢量 udt 表示 S （坡印亭矢量） 

二 光是电磁波 可见光七彩颜色的波长和频率范围 光色 波长(nm) 频率(Hz) 中心波长(nm) 红 760~622 3.9×104-4.8×104 660 橙 622~597 4.8×1045.0×1014 610 黄 597~577 5.0×104~5.4×104 570 绿 577~492 5.4×1014~6.1×104 540 青 492470 6.1×104~6.4×104 480 兰 470~455 6.4×104≈6.6×1014 460 紫 455~400 6.6×104~75×104 430

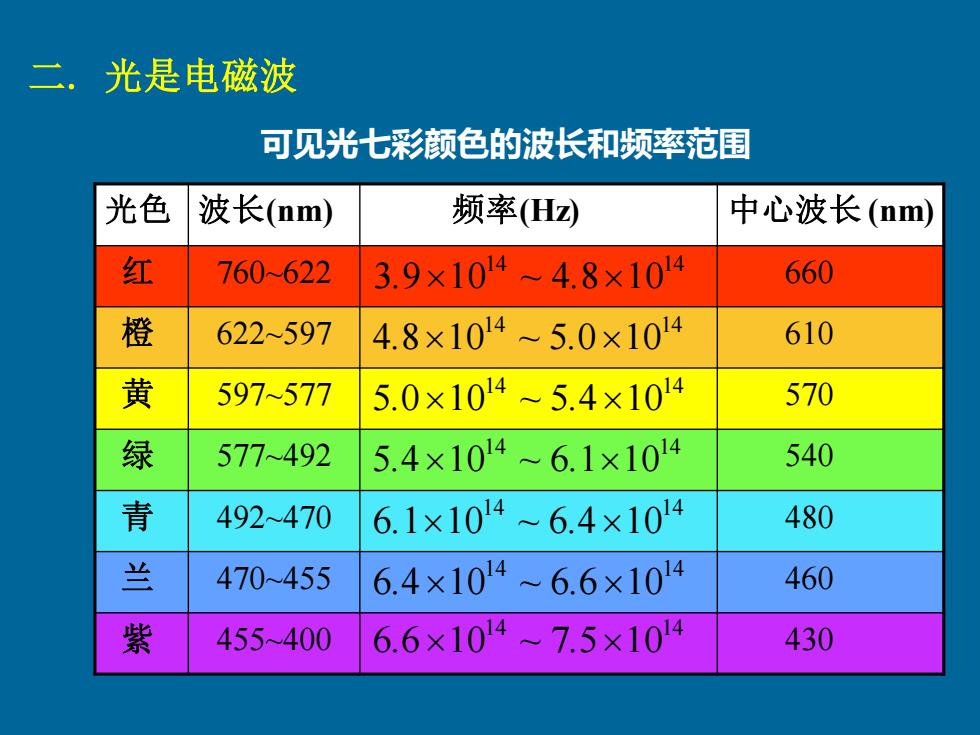
二. 光是电磁波 光色 波长(nm) 频率(Hz) 中心波长 (nm) 红 760~622 660 橙 622~597 610 黄 597~577 570 绿 577~492 540 青 492~470 480 兰 470~455 460 紫 455~400 430 14 14 3.910 ~ 4.810 14 14 4.810 ~ 5.010 14 14 5.010 ~ 5.410 14 14 5.410 ~ 6.110 14 14 6.110 ~ 6.410 14 14 6.410 ~ 6.610 14 14 6.610 ~ 7.510 可见光七彩颜色的波长和频率范围

§14.2光源光波的叠加 一，光源 (1)热辐射 (⑤)同步辐射光源 (2)电致发光 自发 (6激光光源 (3)光致发光 射 受激辐射 (④)化学发光 波列 自发辐射 能级跃迁 E,-E/h 波列长L=xc MM- 非相干（不同原子发的光） 非相干（同一原子先后发的光）

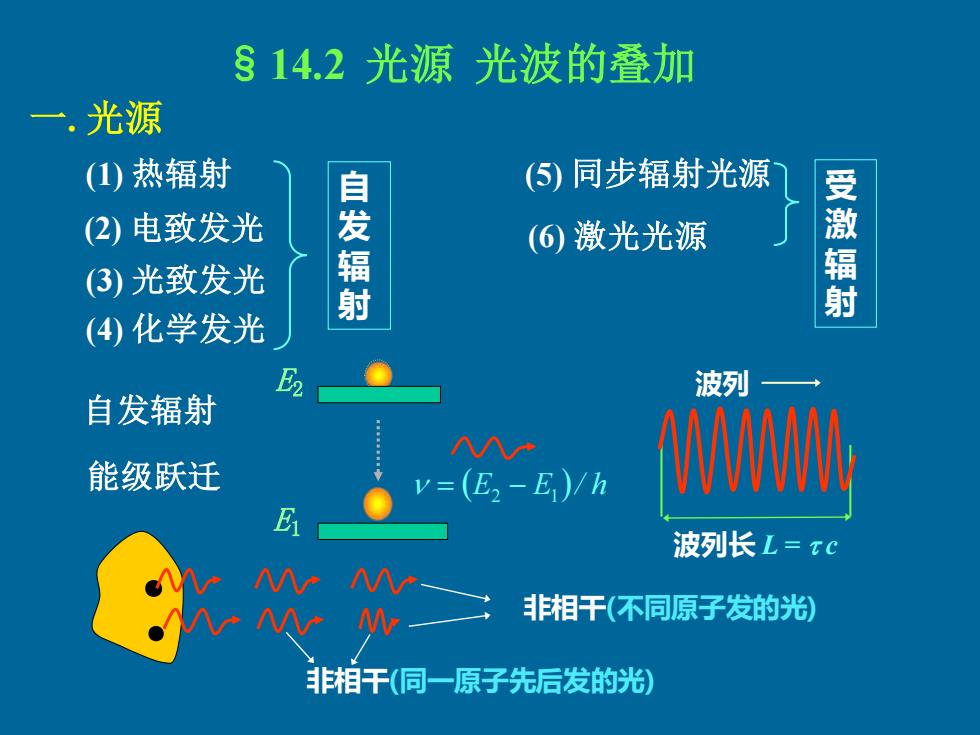
§14.2 光源 光波的叠加 一. 光源 (1) 热辐射 (2) 电致发光 (3) 光致发光 (4) 化学发光 能级跃迁 波列 波列长 L =  c 自 发 辐 射 非相干(不同原子发的光) 非相干(同一原子先后发的光) . . (5) 同步辐射光源 (6) 激光光源 受 激 辐 射 自发辐射 E2 E1  = (E2 − E1 )/ h

二，光波的叠加 月=瓦no@1-2g+） E2 =Eo2cos(@t- Ep=E+E, E形=E+E+2E·E? 光强 Ip=11+12+2 当干涉项2=0,非相干叠加 当干涉项2≠0，相干叠加 2 E·E=Eca+@,+g+g)-or+@5个 +cos(@-or+(g-0,)-0i-o5]}

· 二.光波的叠加 cos( ) 1 1 1 1 01 1   =  − + c r E E t   cos( ) 2 2 2 2 02 2   =  − + c r E E t   EP E1 E2    = + 1 2 2 2 2 1 2 EP E E 2E E   = + +  I p = I 1 + I 2 + 2  E1  E2    光强 P 1 2 r1 r2 · · 当干涉项 2  E1  E2 = 0   2  E1  E2  0   , 非相干叠加 当干涉项 , 相干叠加 E1  E2 =   {cos[( ) ( ) ] 2 1 1 1 2 2 01 02 1 2 1 2 c r r E E t       +  + + + −   cos[( ) ( ) ]} 1 1 2 2 1 2 1 2 c r r t       − + − + − −

讨论 1.非相干叠加 (1)ELE →=0 (2)0+02 27』s.fco(+r+a+）-@r+@] +cos[o,-or+(g-p,)-0-2]}d=0 即=0 (3)(9-p2)不恒定 →-0 非相干叠加时 Ip=1+1

E1 E2   ⊥ 1 2 0 2 π cos  E1  E2 = E1E2 =   讨论  + +  + + + − t T t c r r E E t T {cos[( ) ( ) ] 2 1 1 1 2 2 01 02 1 2 1 2         cos[( ) ( ) ]}d 0 1 1 2 2 1 2 1 2 = − + − + − − t c r r t       1.非相干叠加 0  E1  E2 =   即 1 2 I I I P = + ( ) 1 −2 不恒定  E1  E2 = 0   非相干叠加时 (1) (2) (3)

2.相千叠加 I=1+I3+2√Il2cos△0 A0=%-02- 0(-5） (1)相长干涉（明）△0=+2kπ， k=0,1,2,3. 1=1mm=1+12+2V1I3 如果11=12=16→1=41% (2)相消干涉（暗）△0=±(2k+1)π， k=01,2,3. 1=1mm=1+12-2V713 如果1=1，=1。→ I=0 3.相干条件、相干光源 相干条件：(1)频率相同(2)相位差恒定(3)光矢量振动方向平行 相干光源：同一原子的同一次发光

2 cos I = I 1 + I 2 + I 1 I 2  (1) 相长干涉（明）  = 2kπ , max 1 2 1 2 I = I = I + I + 2 I I (2) 相消干涉（暗）  = (2k +1)π , min 1 2 1 2 I = I = I + I − 2 I I 2.相干叠加 1 2 0 I = I = I 0 I = 4I 1 2 0 I = I = I I = 0 k = 0,1,2,3. k = 0,1,2,3. c (r r ) 1 2 1 2 −  = − −     如果 如果 相干条件:(1)频率相同(2)相位差恒定(3)光矢量振动方向平行 相干光源:同一原子的同一次发光 3.相干条件、相干光源

§14.3 获得相干光的方法杨氏实验 1.分波阵面法（杨氏实验） 获得相干光的方法 2.分振幅法（薄膜干涉) 一.杨氏实验（分波阵面法） ●实验现象 明条纹位置 明条纹位置 明条纹位置

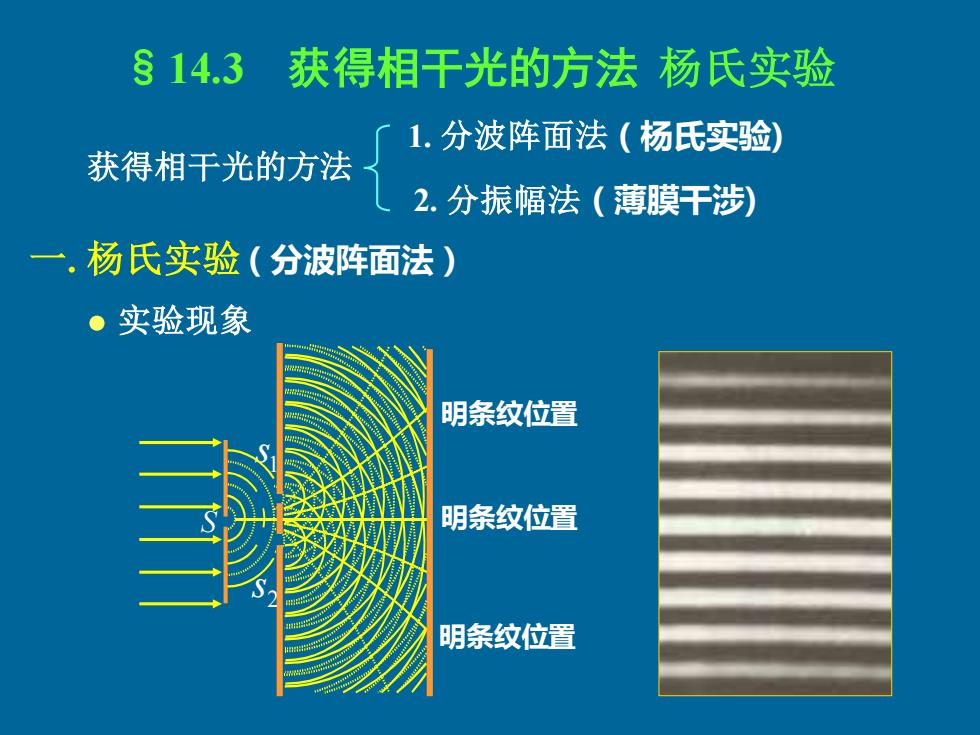
§14.3 获得相干光的方法 杨氏实验 一. 杨氏实验（分波阵面法） 1 s 2 s 明条纹位置 明条纹位置 明条纹位置 获得相干光的方法 1. 分波阵面法（杨氏实验) 2. 分振幅法（薄膜干涉) S • 实验现象