
§12.6温度的微观本质 一,理想气体温度与分子平均平动动能的关系 理想气体分子的平均平动动能为 3kT kT 每个分子平均平动动能只与温度有关,与气体的种类无关。 ◆说明 (1)温度是大量分子热运动平均平动动能的度量.它反映了 宏观量T与微观量的统计平均值之间的关系。 (②)温度是统计概念,是大量分子热运动的集体表现。 对于单个或少数分子来说,温度的概念就失去了意义
§12.6 温度的微观本质 一. 理想气体温度与分子平均平动动能的关系 2 2 1 = v kT kT 2 3 3 2 1 = = 理想气体分子的平均平动动能为 每个分子平均平动动能只与温度有关,与气体的种类无关。 说明 (1) 温度是大量分子热运动平均平动动能的度量.它反映了 宏观量T 与微观量ε的统计平均值之间的关系。 (2) 温度是统计概念,是大量分子热运动的集体表现。 对于单个或少数分子来说,温度的概念就失去了意义

二,理想气体定律的推证 1.阿伏加德罗定律 2 3 p=n8=n. NRT p=nkT VN 在相同的温度和压强下,各种气体的分子数密度相等。 2.道尔顿分压定律 设几种气体贮于一密闭容器中,并处于平衡态,且分子数密 度分别为n1、n2、n3., 则 混合气体的分子数密度为 n=n+n+
p n p = nkT 3 2 = n kT 2 3 3 2 = 二. 理想气体定律的推证 T N R V N 0 = 1. 阿伏加德罗定律 在相同的温度和压强下,各种气体的分子数密度相等。 2. 道尔顿分压定律 设几种气体贮于一密闭容器中,并处于平衡态,且分子数密 度分别为 n1 、n2 、 n3 ., 则 混合气体的分子数密度为 = + + 1 2 n n n

温度相同 81=82=.=8 混合气体的压强为 p= n8 48+ =P+P2+ 混合气体的压强等于各种气体的分压强之和
温度相同 = = . = 1 2 混合气体的压强为 = + + 1 1 2 2 3 2 3 2 n n = + + p1 p2 混合气体的压强等于各种气体的分压强之和。 p n 3 2 =

例有一容积为10cm3的电子管,当温度为300K时用真空泵 抽成高真空,使管内压强为5×10mmHg。 求(1)此时管内气体分子的数目;(2)这些分子的总平动动能。 解(①)由理想气体状态方程得 N= pV5×10-6×133.3×10 =1.61×102 kT 1.38×10-23×300 (2)每个分子平均平动动能 兰kT N个分子总平动动能为 Nc=N.3kT=10*J 2
有一容积为10cm3 的电子管,当温度为300K时用真空泵 抽成高真空,使管内压强为5×10-6 mmHg。 (1) 此时管内气体分子的数目;(2) 这些分子的总平动动能。 解 例 求 1.38 10 300 5 10 133.3 10 23 6 5 = = − − − kT pV N 12 =1.6110 (1) 由理想气体状态方程得 (2) 每个分子平均平动动能 kT 2 3 = N 个分子总平动动能为 10 J 2 3 −8 N = N kT =
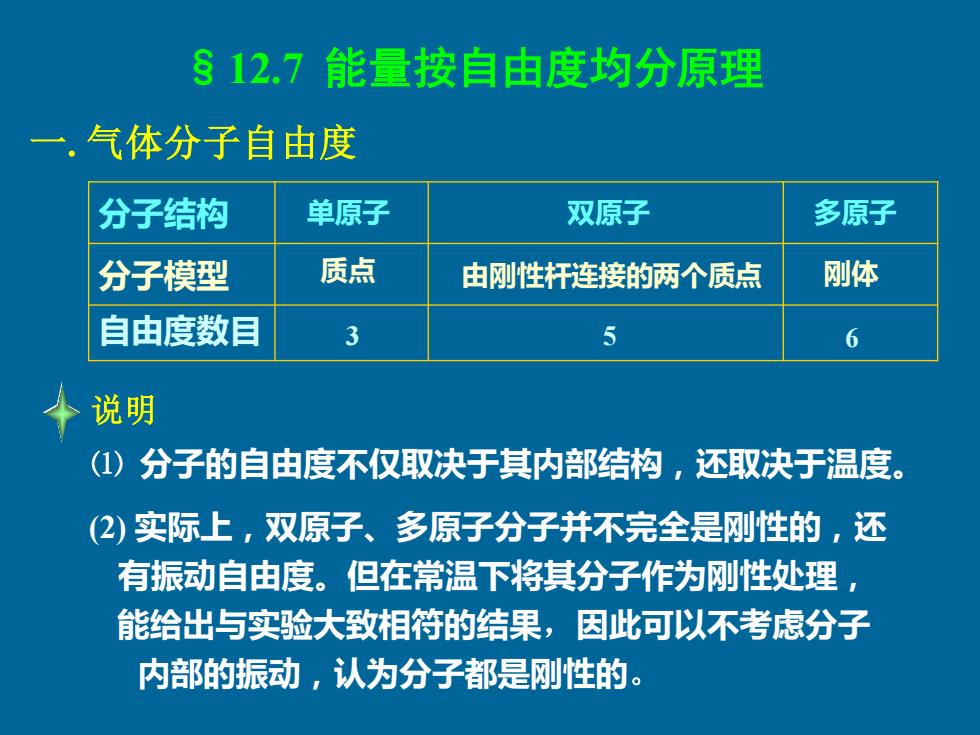
§12.7能量按自由度均分原理 一.气体分子自由度 分子结构 单原子 双原子 多原子 分子模型 质点 由刚性杆连接的两个质点 刚体 自由度数目 3 5 6 说明 ()分子的自由度不仅取决于其内部结构,还取决于温度。 (2)实际上,双原子、多原子分子并不完全是刚性的,还 有振动自由度。但在常温下将其分子作为刚性处理, 能给出与实验大致相符的结果,因此可以不考虑分子 内部的振动,认为分子都是刚性的
§12.7 能量按自由度均分原理 一. 气体分子自由度 分子结构 分子模型 自由度数目 单原子 双原子 多原子 说明 ⑴ 分子的自由度不仅取决于其内部结构,还取决于温度。 3 5 6 质点 由刚性杆连接的两个质点 刚体 (2) 实际上,双原子、多原子分子并不完全是刚性的,还 有振动自由度。但在常温下将其分子作为刚性处理, 能给出与实验大致相符的结果,因此可以不考虑分子 内部的振动,认为分子都是刚性的

二,能量按自由度均分定理 理想气体分子的平均平动动能为 由于气体分子运动的无规则性,各自由度没有哪一个是 特殊的,因此,可以认为气体分子的平均平动动能是平 均分配在每一个平动自由度上的
二. 能量按自由度均分定理 理想气体分子的平均平动动能为 kT 2 3 2 1 2 = v = 2 2 2 2 2 1 2 1 2 1 2 1 v = vx + vy + vz x y z kT 2 1 2 1 2 1 2 1 2 2 2 v = v = v = 由于气体分子运动的无规则性,各自由度没有哪一个是 特殊的,因此,可以认为气体分子的平均平动动能是平 均分配在每一个平动自由度上的

在温度为T的平衡状态下,分子的每个自由度的平均动能均 为。kT。这样的能量分配原则称为能量按自由度均分定理 2 说明 (1)能量按自由度均分是大量分子统计平均的结果,是分子 间的频繁碰撞而致。 (2)若某种气体分子具有t个平动自由度和r个转动自由度, 、个振动自由度,则每个气体分子的平均总动能为 2) 每个气体分子的平均势能为⊙kT, 因此
在温度为T 的平衡状态下,分子的每个自由度的平均动能均 为 kT 。 2 1 这样的能量分配原则称为能量按自由度均分定理 (1) 能量按自由度均分是大量分子统计平均的结果,是分子 间的频繁碰撞而致。 说明 (2) 若某种气体分子具有t 个平动自由度和r 个转动自由度, s 个振动自由度, (t r s)kT 2 1 + + 则每个气体分子的平均总动能为 每个气体分子的平均势能为 kT , s 2 因此

每个气体分子的平均总能量为 2+r+27=7 对于刚性分子 S=0 气体分子的平均总动能等于气体分子的平均总能量。即为 三.理想气体的内能 ·内能系统中与热现象有关的那部分能量 ·理想气体的内能气体中所有分子各种形式动能和分子 内原子间振动势能的总和
kT i t r s kT 2 ( 2 ) 2 1 + + = 每个气体分子的平均总能量为 气体分子的平均总动能等于气体分子的平均总能量。即为 (t r)kT 2 1 + 对于刚性分子 三. 理想气体的内能 内能 气体中所有分子各种形式动能和分子 内原子间振动势能的总和 理想气体的内能 · · 系统中与热现象有关的那部分能量 s = 0

每个气体分子的平均总能量为 1mol理想气体的内能为 E=l vmol理想气体的内能为 E= m I :V- M2 说明 一定质量的理想气体内能完全取决于分子运动的自由度数 和气体的温度,而与气体的体积和压强无关。对于给定气 体,是确定的,所以其内能就只与温度有关,这与宏观 的实验观测结果是一致的。 四.理想气体的摩尔热容 理想气体的定体摩尔热容为 dE C R
1mol 理想气体的内能为 每个气体分子的平均总能量为 RT i kT i E N 2 2 = 0 = RT i RT i M m E 2 2 νmol 理想气体的内能为 = = kT i 2 说明 一定质量的理想气体内能完全取决于分子运动的自由度数 和气体的温度,而与气体的体积和压强无关。对于给定气 体,i 是确定的,所以其内能就只与温度有关,这与宏观 的实验观测结果是一致的。 四. 理想气体的摩尔热容 理想气体的定体摩尔热容为 R i T E CV d 2 d = =

理想气体的定压摩尔热容为 Cp=Cy+R=(I+2R 比热容比为Y= Cp i+2 1mol理想气体的内能变化为 AE=RAT-CAT mol理想气体的内能变化为 AE=vC△7
理想气体的定压摩尔热容为 R i Cp CV R 2 ( + 2) = + = i i C C V p + 2 比热容比为 = = 1mol 理想气体的内能变化为 R T C T i E = = V 2 νmol 理想气体的内能变化为 E =CVT