
第4章冲量和动量 我国舰艇上发射远程导弹实验
第4章 冲量和动量 我国舰艇上发射远程导弹实验
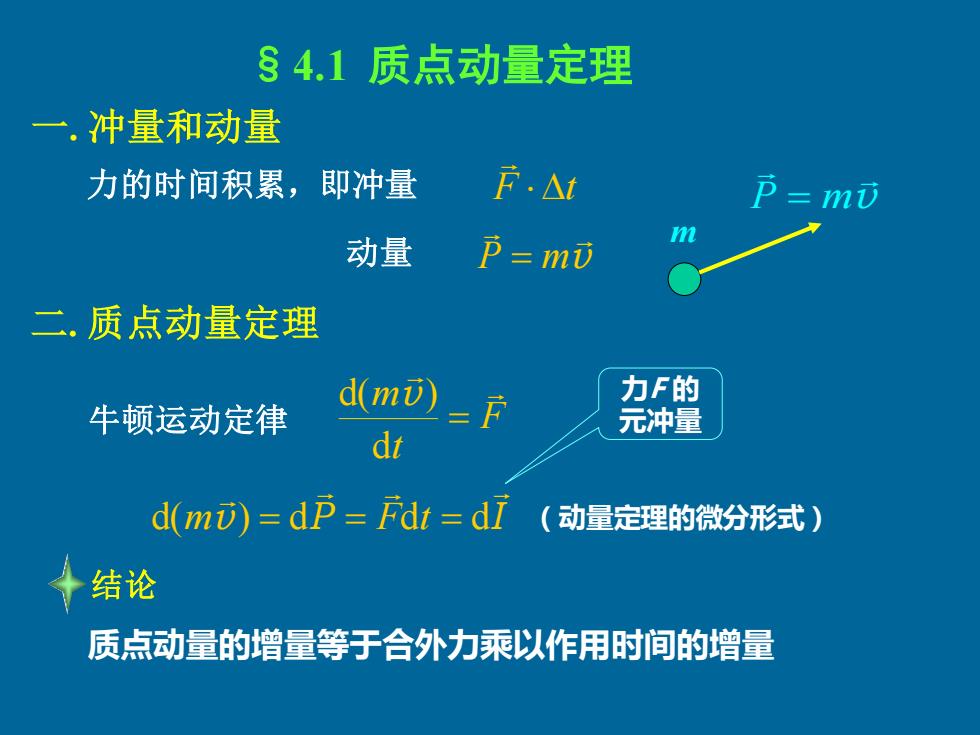
§4.1质点动量定理 一.冲量和动量 力的时间积累,即冲量 F.△1 P=mi 动量 p=mi 二.质点动量定理 d(mi) 力F的 牛顿运动定律 元冲量 dt d(m)=dP=Fd=d7(动量定理的微分形式) 十结论 质点动量的增量等于合外力乘以作用时间的增量
§4.1 质点动量定理 力的时间积累,即冲量 F t m v 动量 P = m 牛顿运动定律 F t m = d d( v) v P I d(m ) = d = Fdt = d 结论 力F 的 元冲量 一. 冲量和动量 二. 质点动量定理 v P = m 质点动量的增量等于合外力乘以作用时间的增量 (动量定理的微分形式)

nv. 对一段有限时间有 m元,一m心=∫Fd(动量定理积分形式) 质点动量的增量等于合力对质点作 用的冲量一 质点动量定理 mi 八1 ◆讨论 mv, ()物理意义:质点动量的变化依赖于作用力的时间累积过程 合力对质点作用的冲量→质点动量矢量的变化 (②)矢量性:冲量的方向与动量的增量方向相同
• • 对一段有限时间有 − = 2 1 2 1 d t t m m F t v v x y z O 质点动量的增量等于合力对质点作 用的冲量 —— 质点动量定理 v1 m v2 m v1 m v2 m (1) 物理意义:质点动量的变化依赖于作用力的时间累积过程 合力对质点作用的冲量 质点动量矢量的变化 (2) 矢量性:冲量的方向与动量的增量方向相同 讨论 F F (动量定理积分形式) I
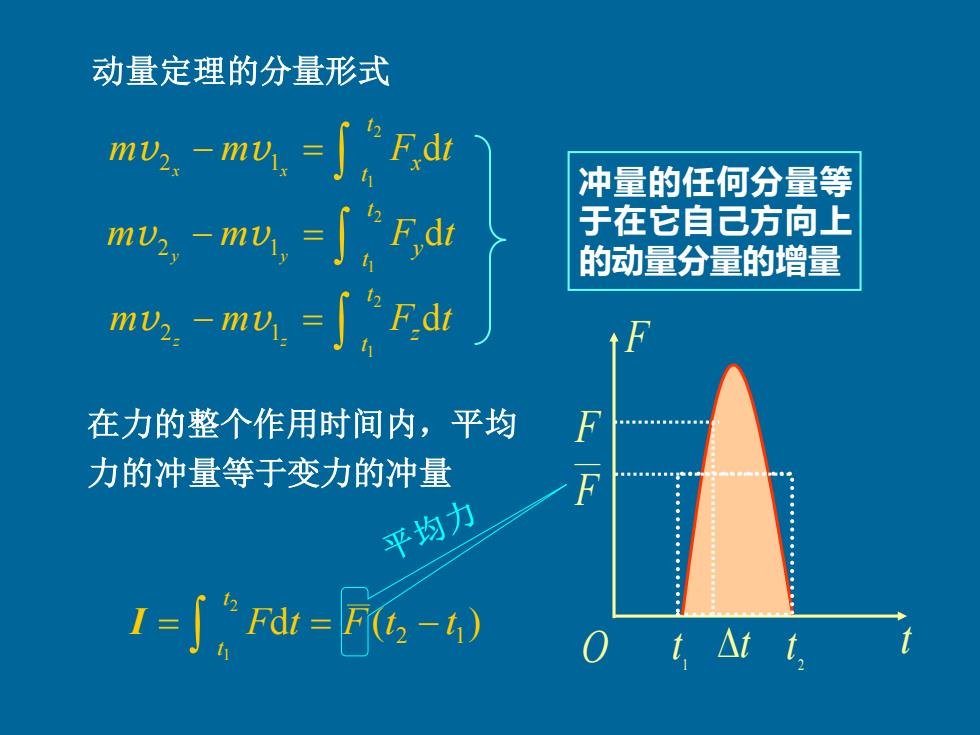
动量定理的分量形式 m,-mu=∫,Fd 冲量的任何分量等 mv,-mv,=∫Fd 于在它自己方向上 的动量分量的增量 mv,.-mv ="Fdt 在力的整个作用时间内,平均 力的冲量等于变力的冲量 平均力 I=∫Fd=F6,-) △tt
− = − = − = 2 1 2 1 2 1 d d d 2 1 2 1 2 1 t t z t t y t t x m m F t m m F t m m F t z z y y x x v v v v v v 在力的整个作用时间内,平均 力的冲量等于变力的冲量 d ( ) 2 1 2 1 F t F t t t t = = − I F F t F O 1 t 2 t t 冲量的任何分量等 于在它自己方向上 的动量分量的增量 动量定理的分量形式
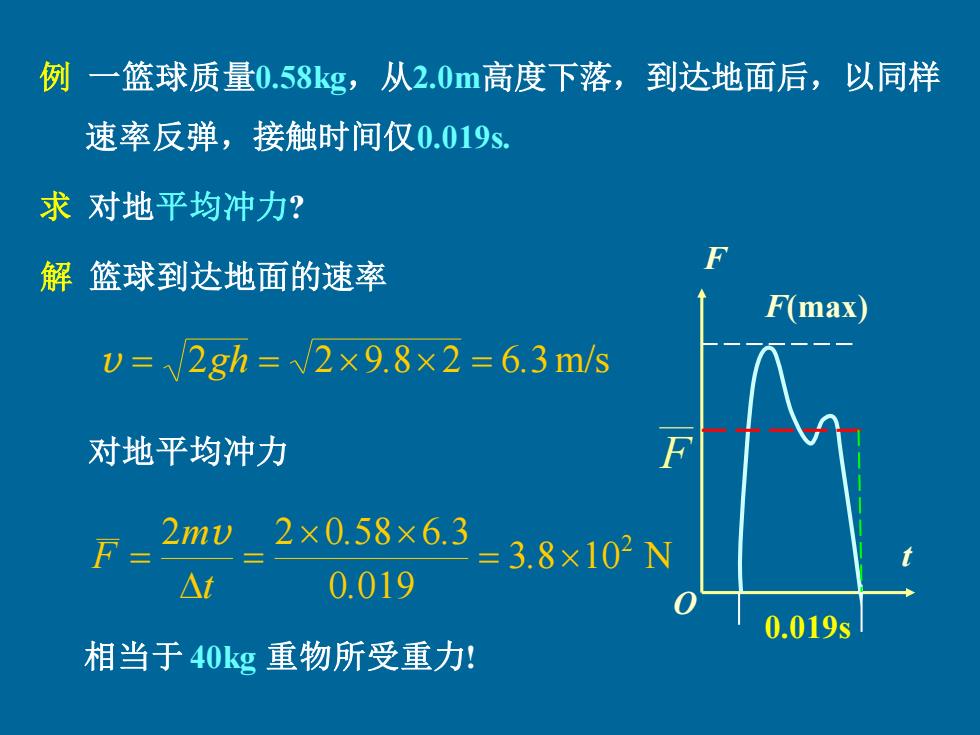
例 一篮球质量0.58kg,从2.0m高度下落,到达地面后,以同样 速率反弹,接触时间仅0.019s 求对地平均冲力? 解篮球到达地面的速率 F(max) v=√2gh=√2×9.8×2=6.3m/s 对地平均冲力 F= 2mv2×0.58×6.3 =3.8×10N △t 0.019 0.019s 相当于40kg重物所受重力:
例 一篮球质量0.58kg,从2.0m高度下落,到达地面后,以同样 解 篮球到达地面的速率 v = 2gh = 29.8 2 = 6.3m/s 3 8 10 N 0 019 2 2 0 58 6 3 2 = = = . . . . t m F v 对地平均冲力 t F(max) F 0.019s O F 相当于 40kg 重物所受重力! 速率反弹,接触时间仅0.019s. 求 对地平均冲力?

例质量为m的匀质链条,全长为L, 开始时,下端与地面的距离为,当链 条自由下落在地面上时 求链条下落在地面上的长度为1<L)时,地面 所受链条的作用力? 解设 m,=1= 链条在此时的速度 w=√2gU+h dm 根据动量定理 -fdt =0-(Audt)u v=w2=2mU+h8=/ dt 地面受力 F=f'+mg= m(31+2h)g
例 质量为 m 的匀质链条,全长为L, 开始时,下端与地面的距离为h , 当链 条自由下落在地面上时 所受链条的作用力? L h 解 设 l L m m l l = = 链条在此时的速度 v = 2g(l + h) 根据动量定理 − fdt = 0 − (vdt)v f' L m l h g t t f = + = = = 2 ( ) d d 2 v v v 地面受力 m l h g L m F = f '+mlg = (3 + 2 ) 求 链条下落在地面上的长度为l ( l<L )时,地面 dm
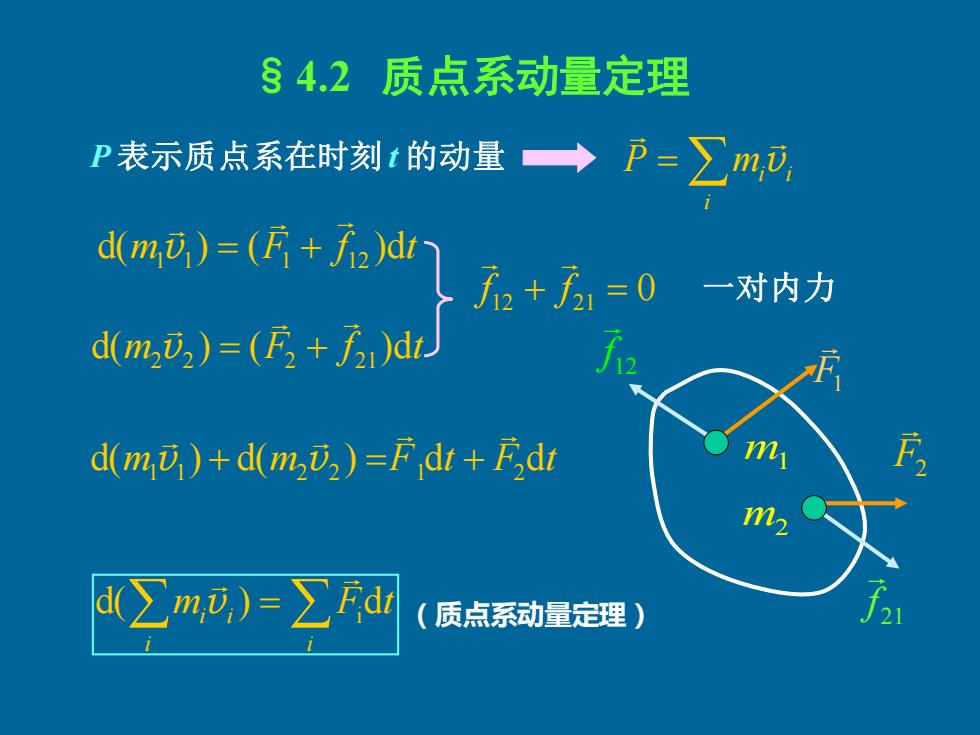
§4.2 质点系动量定理 P表示质点系在时刻?的动量→P=∑m网 dm)=(R+7:e+a=0 一对内力 dm,亚)=(E+方)d d(m)+d(mv,)=F dt+Fdi d(∑m,D)=∑Fd (质点系动量定理)
§4.2 质点系动量定理 P 表示质点系在时刻 t 的动量 = i P mivi d(m ) (F f )dt 1 1 1 12 v = + d(m ) (F f )dt 2 2 2 21 v = + d(m ) d(m ) F dt F dt 1 1 2 2 1 2 v + v = + = i i i i d( m ) Fdt i v m1 m2 12 f 21 f F1 F2 f 12 + f 21 = 0 (质点系动量定理) 一对内力

直角坐标系: d∑mv)=∑Fad d∑mv)=∑F,d d∑mu)=∑F.d 在有限时间内: ∑m西-∑m0=∑∫Fd 某段时间内,质点系动量的增量,等于作用在质点系上所 有外力在同一时间内的冲量的矢量和一质点系动量定理 十说明 (1)只有外力可改变系统的总动量 (2)内力可改变系统内单个质点的动量 内部作用复杂
= = = i iz i i iz i iy i i iy i ix i i ix m F t m F t m F t d( ) d d( ) d d( ) d v v v 直角坐标系: 在有限时间内: (1) 只有外力可改变系统的总动量 (2) 内力可改变系统内单个质点的动量 —— 内部作用复杂 − = i t t i i i i i i i m m F t 0 d 0 v v 说明 某段时间内,质点系动量的增量,等于作用在质点系上所 有外力在同一时间内的冲量的矢量和 ——质点系动量定理

例 一粒子弹水平地穿过并排静止放置在光滑水平面上的木块, 已知两木块的质量分别为m,%2,子弹穿过两木块的时间 各为△,△?,设子弹在木块中所受的阻力为恒力F 求子弹穿过后,两木块各以多大速度运动 解子弹穿过第一木块时,两木块速 度相同,均为1 F△t1=(m,+m)y-0 子弹穿过第二木块后,第二木块速度变为山 F△12=mU2-m3V 解得 F△t F△t V, m1+m3 m +m m
一粒子弹水平地穿过并排静止放置在光滑水平面上的木块, 已知两木块的质量分别为m1 , m2 ,子弹穿过两木块的时间 各为 t1 , t2 ,设子弹在木块中所受的阻力为恒力F ( ) 0 Ft1 = m1 + m2 v1 − 2 m2v2 m2v1 Ft = − 1 2 1 1 m m F t + v = 2 2 1 2 1 2 m F t m m F t + + v = 子弹穿过第一木块时,两木块速 度相同,均为v1 子弹穿过第二木块后,第二木块速度变为v2 例 解 求 子弹穿过后,两木块各以多大速度运动 解得

§4.3质点系动量守恒定律 当 ∑=0→ d(∑mp,)=0 质点系动量守恒定律 (∑m,西)=常矢量 动量守恒的分量表述 F,=0→ ∑m,va)=P=常量 F,=0→ ∑m心n)=卫=常量 F=0→∑m,v))=P=常量 说明 ()动量守恒定律适用于惯性系 (2)动量守恒定律也适用于高速,微观领域
§4.3 质点系动量守恒定律 当 = 0 i Fi d( ) = 0 mivi (mivi) = 常矢量 动量守恒的分量表述 (1) 动量守恒定律适用于惯性系 ( ) ( ) ( ) 常量 常量 常量 = = = = = = = = = z i iz z y i iy y x i ix x F m P F m P F m P v v v 0 0 0 质点系动量守恒定律 说明 (2) 动量守恒定律也适用于高速,微观领域