
第十八章光的衍射 §18.1光的衍涉现象惠更斯-菲涅耳原理 一光的衍射现象 在圆孔摘缝或其他障碍物都很小的情况下,由于它的限制光波的 波阵面,结果有光进入影内并且应外的光强分布也不均匀,这是光的 直线传播定律不能解释的,我们称这种现象为光的衍涉(绕射) 二.惠更斯一菲涅尔原理 从同一波阵面上各点的发出的波,经传播而在空间某点相遇时, 也可相互叠加而产生干涉现象(经过这样发展了惠更斯原理)称为惠 一菲原理。 利用以上原理 ds发出的光在P点产生的振动 由xb@m克 r 成y=ek@sm2-克地 r 其中:k(a)为随a角增大而缓慢减小的函数,c为比例常数 y=jay=e@m2宁-克地 (a) 若波阵面上各点的振幅有一定的分布,且分布函数为(s) 则波阵面s在P点的产生的振动 y-女-ea6ssm2a-克 (b) r 一般来说,(a)和(b)式是相当复杂的积分
第十八章 光的衍射 §1 8 .1 光的衍涉现象 惠更斯-菲涅耳原理 一 光的衍射现象 在 圆 孔 摘 缝或 其 他 障 碍 物 都 很 小 的 情况 下 , 由 于 它 的 限 制 光 波的 波 阵 面 , 结果 有 光 进 入 影 内 并 且 应外 的 光 强 分 布 也 不 均 匀, 这 是 光 的 直线传播定律 不能 解 释 的 ,我 们 称 这 种现 象 为 光 的 衍涉 ( 绕 射 ) 二 .惠更斯—菲涅 尔 原 理 从 同一 波 阵 面 上各 点 的 发 出的 波, 经 传 播 而 在空 间 某 点 相遇 时 , 也 可 相 互 叠加 而 产 生 干 涉 现 象 ( 经过 这 样 发 展 了 惠 更 斯 原理 ) 称 为 惠 —菲原理。 利用以上原理 : ds 发出的光在 P 点 产 生 的振 动 ) r T t sin( r ds k( ) dy − 或 )ds r T t sin 2 ( r k( ) dy c − = 其中:k(а)为 随 а 角增 大 而 缓 慢减 小 的 函 数 , c 为比例常数 )ds r T t sin 2 ( r k( ) y dy c s s − = = (a) 若波阵面上各 点的 振 幅 有 一定 的 分 布 ,且 分 布 函 数 为 a(s ) i 则 波阵面 s 在 P 点的产 生 的 振 动 − = = s i s )ds r T t sin 2 ( r a(s )k( ) y dy c (b) 一般来说,(a)和 ( b) 式 是 相 当复 杂 的 积 分
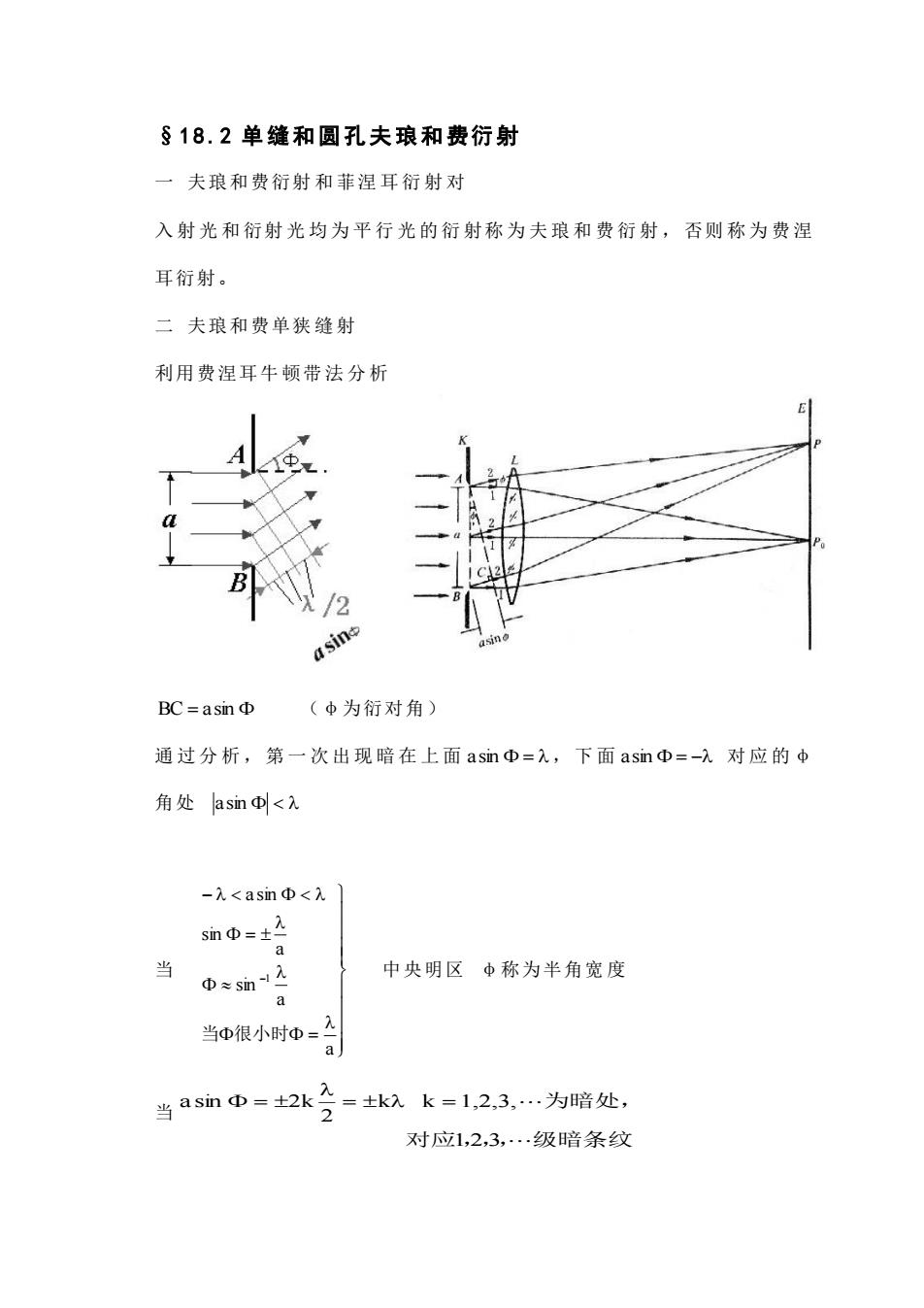
§18.2单缝和圆孔夫琅和费衍射 一夫琅和费衍射和菲涅耳衍射对 入射光和衍射光均为平行光的衍射称为夫琅和费衍射,否则称为费涅 耳衍射。 二夫琅和费单狭缝射 利用费涅耳牛顿带法分析 asine BC=asinΦ (中为衍对角) 通过分析,第一次出现暗在上面asm中=入,下面asn中=-入对应的中 角处asin可< -入<asin中<λ smΦ=±2 当 0m合 中央明区中称为半角宽度 当0限小9神-合 当asm=2k含=士k以k=1,23为暗处。 对应1,23,.级暗条纹
§1 8 .2 单缝和圆孔夫琅和费衍射 一 夫琅和费衍射 和 菲涅 耳衍射对 入 射 光 和 衍射 光 均 为 平 行 光 的 衍 射称 为 夫 琅 和 费 衍 射 , 否则 称 为 费 涅 耳衍射。 二 夫琅和费单狭 缝 射 利用费涅耳牛 顿带 法 分 析 BC = asin (φ为衍对角) 通过分析,第一次出现暗在上面 a sin = ,下面 asin = − 对应的φ 角处 a sin 当 = = − − a a sin a sin a sin 1 当 很小时 中央明区 φ称为半角宽 度 当 对应 , 级暗条纹 为暗处, 1 2 3 k k 1,2,3, 2 a sin 2k = = =

当asin d=(2k+)号k=1,2,3.为明条纹中心处, 对应1,2,3,.级明条纹 暗条纹sn中=址2 k=12,3. 从上解出 明条纹s血=+会k=123 亮度 B.P:P 衍射各样特点: ①中央量条纹的宽度两倍于各次最大的亮条纹的宽度,且绝大部分光 能都落在中央条纹上。 ②暗条纹是等间隔的,而次最大(近似等间隔)不等间隔。 ③当入射光为白光时,除中央明区为白色条纹外,两侧为紫到红排列 的彩色的衍射光谱。 ④当入一定时,a愈小,衍射愈显著,当a<入时,入射光按直线传播。 §18.3衍射光栅 一·光栅的构造
当 ( ) 对应 , 级明条纹 为明条纹中心处, 1 2 3 k 1,2,3, 2 a sin 2k 1 = = + 从上解出 ( ) k 1,2,3, 2a sin 2k 1 k 1,2,3, a sin k = = + = == 明条纹 暗条纹 衍射各样特点: ①中央量条纹的宽度两倍于各次最大的亮条纹的宽度,且绝大部分光 能都落在中央 条纹 上 。 ②暗条纹是等 间隔 的 , 而 次最 大 ( 近 似等 间 隔 ) 不 等间 隔 。 ③当入射光为白光时,除中央明区为白色条纹外,两侧为紫到红排列 的彩色的衍射 光谱 。 ④ 当 一定 时 ,a 愈小 ,衍 射 愈显 著 ,当 a 时,入 射光 按 直 线 传 播。 §1 8 .3 衍射光栅 一 . 光栅的构造

分透射和反射光栅 设光栅缝宽为a,每刻痕的宽度为b,则(a+b称为光栅常数。 若每厘米刻痕为5000条,则光栅常数为 a+b=1/5000cm=2×10mm 二.光栅的衍射条纹 分析知:光栅条纹是干涉和衍射的综 合结果,所有的狭缝的衍射条纹在屏幕上 相互重合。 则衍射暗纹位置:asin中=k'久(k'=l,2,3暗 相邻缝干涉明纹位置(明纹主极大位置) (a+b)sim中=±kk=0,1,2)明 (2) 称为光栅公式.干涉条纹要变到衍射条纹的调制 讨论一具体情形: 设某光栅缝数N=4a+b=4aa为缝宽 入中以(a+b)smn中=4asin中为横坐标,以光强为纵坐标作图 asin中=±k'久 单缝衍射: 4asn中=士k'4.k'=L2,3衍射暗纹 中央明纹宽度:4asn=4 光棚衍射 光强曲线 单缝衍射 轮廓线 0 4
分透射和反射光 栅 设光栅缝宽为 a, 每刻 痕 的 宽 度为 b ,则(a +b 称 为光 栅 常 数 。 若每厘米刻痕为 50 00 条 , 则 光 栅常 数 为 a+b=1/5000cm=2×1 0- 3 mm 二 . 光栅的衍射条纹 分析知:光栅 条纹 是 干 涉 和衍 射 的 综 合结果,所有 的狭 缝 的 衍 射条 纹 在 屏 幕上 相互重合。 则衍射暗纹位 置: a sin k (k 1,2,3 ) (1) = / / = 暗 相邻缝干涉明 纹位 置 ( 明 纹主 极 大 位 置) (a + b)sin = k (k = 0,1,2) 明 (2) 称为光栅公式.干 涉 条纹 要 变 到 衍射 条 纹 的 调 制. 讨论一具体情形: 设某光栅缝数 N=4 a+b=4a a 为缝宽 λφ以 (a + b)sin = 4a sin 为横坐 标, 以 光 强 为纵 坐 标 作 图 单缝衍射: 4a sin k 4 (k 1,2,3 ) a sin k / / / = = 衍射暗纹 = 中央明纹宽度 : 4a sin = 4

对干涉(a+b)sin中=士k入k=0,1,2)明 4asn中=±k 但两明纹之间,出现暗的可能较多,对两主极大之间即位相从0~2Π 之间,有相邻位相差为Π/2,Π,3Π/2时均可出现极小。 在两主极大之间有N-1=4-1=3条暗纹 当某一·同时满足 asm中=k'久'=l2,3) (a+b)sin中-±k2 (k-0,12)时出现缺级 →k=a+bk 缺级数为k a 例:当a+b=4a时,a+b/a=4 k=4,8,12.发生缺级 三.衍射光谱 从(2)式可知,除k=0外,=1,2,.明纹的位置与入有关,两 侧按由紫到红展开,形成光谱,称为光栅光谱。 §18.4夫琅和费圆孔衍射:光学仪器的分辨率 一·夫琅和费圆孔衍射
对干涉 (a + b)sin = k (k = 0,1,2) 明 4a sin = k 但 两明 纹 之 间, 出 现 暗的 可 能 较 多, 对 两主 极 大 之 间即 位 相 从 0~2П 之间,有相邻 位相 差 为 П/ 2,П,3П /2 时均 可 出 现 极小 。 在两主极大之 间有 N-1 =4 -1=3 条暗纹 当某一 同时满 足 a sin k (k 1,2,3 ) = / / = (a + b)sin = k (k = 0,1,2) 时出现缺级 / k a a b k + = 缺级数为 k 例:当 a+b=4a 时, a+b /a =4 k=4,8,12.发生 缺 级 三 . 衍射光谱 从 ( 2) 式 可 知 ,除 k =0 外, =1,2, . 明 纹 的位 置 与 λ 有关 , 两 侧按由紫到红 展开 , 形 成 光谱 , 称 为 光栅 光 谱 。 §1 8 .4 夫琅和费圆孔衍射:光学仪器的分辨率 一 .夫琅和费圆 孔衍 射
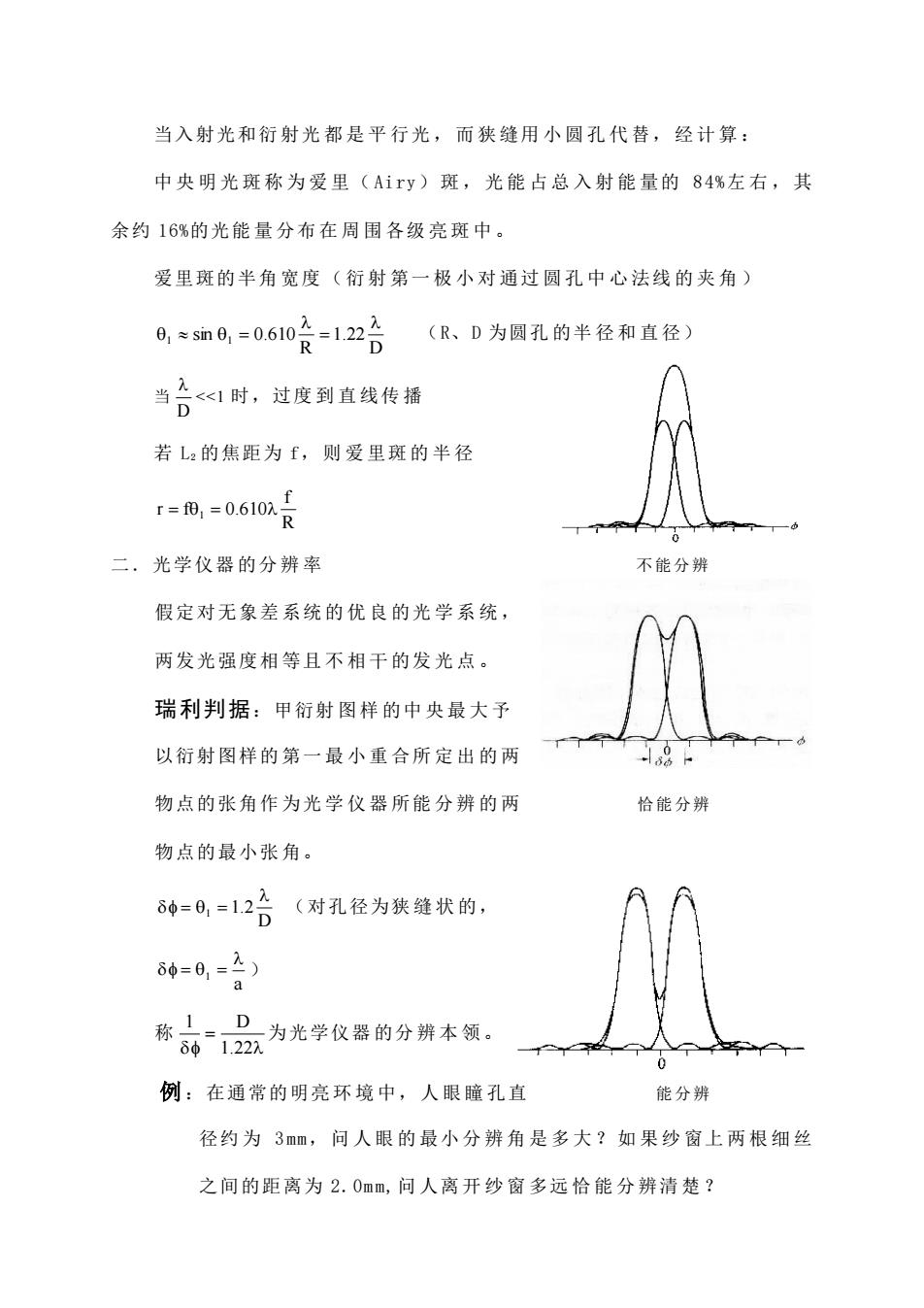
当入射光和衍射光都是平行光,而狭缝用小圆孔代替,经计算: 中央明光斑称为爱里(Airy)斑,光能占总入射能量的84%左右,其 余约16%的光能量分布在周围各级亮斑中。 爱里斑的半角宽度(衍射第一极小对通过圆孔中心法线的夹角) 0,*m0,=0610t=126 (R、D为圆孔的半径和直径) 当。<1时,过度到直线传播 若L:的焦距为f,则爱里斑的半径 r=0,=0610景 二·光学仪器的分辨率 不能分辨 假定对无象差系统的优良的光学系统, 两发光强度相等且不相干的发光点。 瑞利判据:甲衍射图样的中央最大予 以衍射图样的第一最小重合所定出的两 物点的张角作为光学仪器所能分辨的两 恰能分辨 物点的最小张角。 80=0=12哈(对孔径为获缝状的。 80=0=2) a 疹动品为光学仅器的分辨本领。 例:在通常的明亮环境中,人眼瞳孔直 能分辨 径约为3mm,问人眼的最小分辨角是多大?如果纱窗上两根细丝 之间的距离为2.0mm,问人离开纱窗多远恰能分辨清楚?
当入射光和衍 射光 都 是 平 行光 , 而 狭 缝用 小 圆 孔 代 替, 经 计 算 : 中央明光斑称为爱里( Ai ry)斑,光能占总入射能量的 8 4%左右,其 余约 16%的光能 量 分布 在 周 围 各级 亮 斑 中 。 爱里斑的半角 宽度 ( 衍 射 第一 极 小 对 通过 圆 孔 中 心 法线 的 夹 角 ) D 1.22 R 1 sin 1 0.610 = = (R、D 为圆孔 的半 径 和 直 径) 当 D <<1 时,过度 到 直 线传 播 若 L2 的焦距为 f,则爱里斑的半径 R f r = f1 = 0.610 二.光学仪器 的分 辨 率 不能分辨 假定对无象差 系统 的 优 良 的光 学 系 统 , 两发光强度相 等且 不 相 干 的发 光 点 。 瑞利判据:甲衍射 图 样 的中 央 最 大 予 以衍射图样的 第一 最 小 重 合所 定 出 的 两 物点的张角作 为光 学 仪 器 所能 分 辨 的 两 恰能分辨 物点的最小张 角。 D 1 1.2 = = (对孔径为狭 缝 状 的, a 1 = = ) 称 = 1.22 1 D 为光学仪器 的分 辨 本 领 。 例:在通常的明亮 环 境 中, 人 眼 瞳 孔直 能分辨 径约 为 3 mm, 问 人 眼 的 最小 分 辨 角 是 多 大 ? 如 果 纱 窗上 两 根 细 丝 之间的距离为 2. 0m m,问 人离 开 纱 窗 多远 恰 能 分 辨清 楚 ?

解:以视觉感受最灵敏的黄绿光来讨论,波长λ=550nm,人眼的最小 分辨角 =1哈-18=2wad 设人离开纱窗的距离为5,纱窗上相邻两根细丝的间距为,对人眼 来说,张角0为0:号 当恰能分辨时,应有日=日。 于是 0≈=2.0x10-3 22×10m=91m 即人眼能分辨纱窗细丝的最远距离约为9m. 本章小结: 1.干涉和衍射的区别和联系,惠更斯一一菲涅耳原理 2.单缝夫琅和费衍射(半波带法),条纹的特点要掌握 (1)平行光垂直入射 (2)asmD=2k+02k=123.明 asinΦ=±k入 k=1,2,3,.暗 这里k≠0 在暗纹公式中,k=0,实际上对应中央极大的中心 在明纹公式中,k=0,asin中=2/2,实际上对应中央明条纹内极不 最亮,也不最暗的点。 当平行光以Ψ角入射时,两边缘处已有asmp的光程差 ·asinΨ+snφ)=±k2 暗 asnΨ+sm)=(2k+)号明k=12. 且入射光和衍射光单缝法线两侧时,◆取负值,入射光和衍射光
解 :以 视 觉 感 受最 灵 敏 的 黄绿 光 来 讨 论,波 长 λ= 550 nm,人 眼的 最 小 分辨角 rad 2.2 10 rad 3.0 10 550 10 1.22 D 1.22 4 3 9 R − − − = = = 设人 离 开 纱 窗的 距 离 为 s,纱 窗 上 相 邻两 根 细 丝 的 间距 为 ,对人眼 来说,张角 为 s 当恰能分辨时, 应 有 = R 于是 m 9.1m 2.2 10 2.0 10 s 4 3 = = − − 即人眼能分辨纱 窗 细 丝 的最 远 距 离 约为 9m. 本章小结: 1 .干涉和衍射的区别和联系,惠更斯 — —菲涅耳原理 2 .单缝夫琅和费 衍射 ( 半 波 带法 ),条 纹 的 特 点要 掌 握 (1)平行光垂 直 入 射 (2) ( ) 暗 明 a sin k k 1,2,3, k 1,2,3, 2 a sin 2k 1 = = = = + 这里 k≠0 在暗纹公式中 ,k= 0,实 际 上对 应 中 央 极大 的 中 心 在 明纹 公 式 中 ,k =0, a sin = / 2,实际 上 对 应 中央 明 条 纹 内极 不 最亮,也不最 暗的 点 。 当平行光以 角 入射 时 , 两 边缘 处 已 有 a sin 的光 程 差 k 1 2 2 λ a(sin sin ) (2k 1) a(sin sin ) kλ 明 , 暗 + = + = + = 且 入 射 光 和 衍射 光 单 缝 法 线 两 侧 时 , 取负值,入 射 光 和 衍 射光

单缝法线同侧时,中取正值。 这是衍射条纹将发生移动,中央明条纹的中心在沿入射光线方 向的透镜副光轴与屏幕的交点处。 (3)明条纹宽度: 角宽度中央条纹 其他条纹 4,=2 a 线宽度△x。=△pf △x=△of (4)若把装置放入水中,焦距和光程差改变都要考虑 4-0-D2-l304D2=3422 1.54-1.33 △以=2.57△% isND) 3.圆孔的夫琅和费衍射 1半角宽度0=0610哈=12哈 (2)最小分辨角60=12哈 光学仪器分辨率(本领) R=1/80=122 D 4.衍射光栅 (1)光栅方程(垂直入射) (a+b)sn中=kk=0,1,2)明 (2)当入射光是白光时,除中央条纹是白色外,其他条纹都是从紫 到红的彩色光谱。光谱随着级数增加而增宽,在较高级次的光 谱中,有部分要彼此重合
单缝法线同侧 时, 取正值。 这 是 衍 射 条纹 将 发 生 移 动 , 中 央 明 条纹 的 中 心 在 沿 入 射 光 线方 向的透镜副光 轴与 屏 幕 的 交点 处 。 (3)明条纹宽 度 : 角宽度 中央条纹 其他条纹 a 2 0 = a = 线宽度 x f 0 = 0 x = f (4)若把装置放 入 水 中, 焦 距 和 光程 差 改 变 都 要考 虑 ) n f f 2.57 ( f 3.42f 1.54 1.33 1.33 1.54 1 f n n n (n 1) f ' ' = = = − − = − − = 水 空 水 空 空 空 波 波 水 波 水 ( ) 3.圆孔的夫琅和 费衍 射 (1)半角宽度 D 1.22 R 1 0.610 = = (2)最小分辨 角 D 1.22 = 光学仪器分辨率 ( 本 领 ) = = 1.22 D R 1/ 4.衍射光栅 (1)光栅方程 ( 垂直 入 射 ) (a + b)sin = k (k = 0,1,2) 明 (2)当 入射 光 是 白 光 时 ,除 中 央 条 纹是 白 色 外 ,其 他条 纹 都 是 从紫 到 红的 彩 色 光 谱 。光谱 随 着 级 数增 加 而 增 宽 ,在较 高 级 次 的光 谱中,有部分 要彼 此 重 合

(3)由光栅方程 干涉明纹(a+b)sn中=kk=0,12) 衍射暗纹asin中=k'久(k'=l,2,3 当k=a+也k时,k=1,2.发生缺级 即M=a+b,则M、2训、3M.等级缺级 (4)斜入射时,光栅方程为 (a+b(sinΨ+sinφ)=士kk=0,l2. 其中平为入射光与光栅法线的夹角 当入射线与衍射线在法线同侧时,中取正值,反之,中取负值。 例1有一单缝,宽a=0.10mm,在缝后放一焦距为50cm的会聚透镜。用平 行绿光(入=546.0m)垂直照射单缝,n=1.54,n*=1.33 试求:(1)位于透镜焦平面处的屏幕上中央明条纹和两侧任意相邻 两暗条纹之间的距离。 (2)若浸入水中,结果如何? 解:1.由asnp=kk=±1暗 半角宽sm0*g9=名 a 4%=z-x-=28=546m 第k级和第k+1级暗纹之间的距离 4以=xu-8-273m 2.透镜在水中的焦距
(3)由光栅方 程 干涉明纹 (a + b)sin = k (k = 0,1,2) 衍射暗纹 a sin k (k 1,2,3 ) = / / = 当 / k a a b k + = 时,k / =1,2. 发 生 缺级 即 M= a a + b ,则 M、2M、3M.等 级 缺 级 (4)斜入射时 , 光栅 方 程 为 (a + b)(sin + sin ) = kλ k = 0,1,2 其中 为入射光 与光 栅 法 线 的夹 角 当 入射 线 与 衍 射线 在 法 线 同侧 时 , 取 正 值 ,反 之 , 取负 值 。 例 1 有一单 缝 , 宽 a= 0. 10m m,在 缝 后放 一 焦 距 为 5 0c m 的 会 聚 透 镜。 用 平 行绿光( = 546.0nm )垂 直照 射 单 缝 ,n 玻 =1 .5 4,n 水 =1 .33 试求:( 1)位于透镜焦平面处的屏幕上中央明条纹和两侧任意相邻 两暗条纹之间 的距 离 。 (2)若浸入 水中 , 结 果 如何 ? 解:1.由 a sin = k k = 1 暗 5.46mm a f 2 a f k f sin tg 0 1 1 k = = − = = = − 半角宽 第 k 级和第 k+1 级 暗纹 之 间 的 距离 2.73mm a f 0 k 1 k = = + − = 2.透镜在水中的 焦 距

f4-n0-D2=342x050=171m n酸一n水 na sin=k暗 k=,±2 A/=25s入=1404mm A-语A=702m 注意:角宽是原来的1/加k,线宽度与f有关 例2在垂直入射于光栅的平行光中,有入,和入:两种波长。己知入:的第 三级光谱线(即第三级明纹)与入,的第四级光谱线恰好重合在离中央 明条纹为5mm处,且入=4861A,并发现恰好入:的第五级光谱线缺级 透镜f=0.5m。 求:1.入,a+b是多少? 2.光栅最小缝宽a? 3.能观察到入:的多少条光谱线? 解:1. (a+b)sn中=k (a+b)sin中=k,入=k,入 又 名=g4*s中 。b-篇-=1rm 2.第k级缺级时,有(a+b)sn中=k am=a-兰e+) k=l对应最小缝宽a=写a+b)=0388×10cm 3.能观察到的谱线数目取决于能出现的最大级数和缺级
7.02mm na f 14.04mm na f 2 na sin k k 1, 2 f 3.42 0.50 1.71m n n n n 1 f ' / 0 = = = = = = = = − − = 水 水 空 玻 水 水 玻 水 暗 ( ) 注意:角宽是原来的 1/n 水 , 线宽度与 f 有关 例 2 在垂直入射于光 栅 的 平行 光 中 , 有λ 1 和 λ2 两 种 波长 。 已 知 λ1 的第 三 级光 谱 线( 即 第 三 级明 纹 )与 λ2 的 第 四级 光 谱 线 恰 好重 合 在 离 中央 明 条纹 为 5 mm 处,且 λ2= 48 61 0 A ,并 发 现 恰好 λ1 的 第 五 级光 谱 线 缺 级。 透镜 f=0.5m。 求:1.λ1,a+b 是多少? 2.光栅最小缝宽 a? 3.能观察到λ1 的 多 少 条 光谱 线 ? 解:1. (a + b)sin = k 由题意: ( ) 0 2 1 2 1 1 1 2 2 4861 6481A 3 4 k k a b sin k k = = = + = = 又 k 1.94 10 cm f sin k a b tg sin f 2 2 2 2 2 − = = + = = 2.第 k 级缺级时, 有 (a + b)sin = k (a b) 0.388 10 cm 5 1 k 1, a (a b) k k a sin k a / 2 / / − = = + = = = + 对应 最小缝宽 3.能观察到的 谱 线数 目 取 决 于能 出 现 的 最 大级 数 和 缺 级