
第十三章电磁感应 §13-1电磁感应的基本定律 一、电磁感应现象 当穿过一个闭合导体回路所包围的面积内的磁通量发生变化时,在导体回路中就会 产生电流,这种现象称为电磁感应现象(1831年)。 二、楞次定律(1833年) (纯电阻)闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生 的通过回路面积的磁通量,去补偿或反抗引起感应电流的磁通量的变化。 或:感应电流的效果总是反抗引起感应电流的原因。 这里:“效果”可以理解为感应电流激发的磁场,也可以理解为因感应电流出现而引起 的机械作用。“原因”既可以指磁通量的变化,也可指引起磁通量变化的相对运动或回 路的形变。 ▲实质:感应电流取楞次定律所述的方向,是能量守恒和转化定律的必然结果。 例题:楞次定律是能量守恒所必需的。换句话说,如果电磁感应的规律正好与楞次定律 相反,则能量守恒定律不成立。试用简单例子加以说明。 三、法拉第电磁感应定律 导体回路中感应电动势£,的大小与穿过回路的磁通量的变化率心成正比。 d dt 或e=-K dt 对于国际单位制: K=1 dΦ 8,=- (适用于单匝导线组成的回路)
第十三章 电磁感应 §13-1 电磁感应的基本定律 一、电磁感应现象 当穿过一个闭合导体回路所包围的面积内的磁通量发生变化时,在导体回路中就会 产生电流,这种现象称为电磁感应现象(1831 年)。 二、楞次定律(1833 年) (纯电阻)闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生 的通过回路面积的磁通量,去补偿或反抗引起感应电流的磁通量的变化。 或:感应电流的效果总是反抗引起感应电流的原因。 这里:“效果”可以理解为感应电流激发的磁场,也可以理解为因感应电流出现而引起 的机械作用。“原因”既可以指磁通量的变化,也可指引起磁通量变化的相对运动或回 路的形变。 ▲ 实质:感应电流取楞次定律所述的方向,是能量守恒和转化定律的必然结果。 例题:楞次定律是能量守恒所必需的。换句话说,如果电磁感应的规律正好与楞次定律 相反,则能量守恒定律不成立。试用简单例子加以说明。 三、法拉第电磁感应定律 导体回路中感应电动势 i 的大小与穿过回路的磁通量的变化率 d dt 成正比。 i dΦ ε dt 或 i dΦ ε dt = −K 对于国际单位制: K=1 i dΦ ε dt = − (适用于单匝导线组成的回路)

对于多匝线圈串联,每匝的磁通分别为中,中2,“,中 dt dt dt =-m+0,+.0,) 平=④,+中,++Φ、叫做磁通匝链数或全磁通。 若中,相同,均为中,则平=N中 dt ▲感应电动势的方向问题: 规定: 【,回路的正方向→确定ε的正负 2、曲面法线的正方向→确定Φ的正方向方可满足法拉第定律 3、与的关系满足右手法则 如果闭合电路的电阻为R, 当1=1o,中=中;1=4,Φ=中,通过回路中任一截面的感应电量(迁移的电量) ★q=1h=-元=最o。-o,) 例题: 如图,环形螺线管n=5000匝/米, 安=-20安培秒,截面S=2x10米,在环上 再绕一线圈A,N=5匝,R=2.0欧姆 求:1、A中6,及1, 2、2秒内通过A的电量q 解:环内的B≈4l,通过A的D=S
对于多匝线圈串联,每匝的磁通分别为 1 2 , , , N 1 2 N i d d d dt dt dt = − − − − 1 2 ( ) N d dt d dt = − + + = − = + + + 1 2 N 叫做磁通匝链数或全磁通。 若 i 相同,均为 ,则 = N , i d dΦ ε dt dt N = − = − ▲ 感应电动势的方向问题: 规定: 方可满足法拉第定律 与 的关系满足右手法则 曲面法线 的正方向 确定 的正方向 回路 → → 3、 L n 2、 n 1 的正方向 确定 的正负 、 L 如果闭合电路的电阻为 R, 1 i d I R dt = − 当 0 0 1 1 t t t t = = = = , ; , ,通过回路中任一截面的感应电量(迁移的电量) ★ 1 1 0 0 0 1 1 1 ( ) t i t q I dt d R R = = − = − 例题: 如 图 , 环 形 螺 线 管 n=5000 匝 / 米 , 20 / dI dt = − 安培 秒 ,截面 3 2 S 2 10− = 米 。在环上 再绕一线圈 A,N=5 匝, R=2.0 欧姆 求:1、A 中 i 及 i I 2、2 秒内通过 A 的电量 q 解:环内的 B nI 0 ,通过 A 的 0 = nIS

5-小水盟4s图-126r伏特 1=126×10=6.30×10安培 2 9=∫1,dh=6.30x10×2.0=126x103库仑 §13-2在磁场中运动的导线内感应电动势(动性电动势) 一、动生电动势 D=B.S=BII' 59品)=m →8,=Bw方向可由楞次定律得 到(从b指向a) 二、对动生电动势的解释 由金属电子理论: ∫F.=9×B=-ep×B F,=gE=-eE [F.=evB→向下 E=eE→向上 当eE=eBE=B,这时,。-y=El,即因 洛仑兹力作用的结果 6,=E=B与前面结果完全一致。 ▲以上说法与洛仑兹力不作功是否相矛盾呢?不矛盾。以下说明: 总洛仑兹力为:F=-(位+)×B,它与合成速度下+n垂直,不做功 然而分力,于=-(下×B)对电子做正功,形成动生电动势。而另一分力,F=-(下+)×B, 它沿-下方向,做负功。可以证明两功代数和为零,证明如下: F(下+)=0总功率为零
3 0 1.26 10 i d dI N nNS dt dt − = = = 伏特 3 1.26 10 4 6.30 10 2 i I − − = = 安培 2 1 4 3 6.30 10 2.0 1.26 10 t i t q I dt − − = = = 库仑 §13-2 在磁场中运动的导线内感应电动势(动生电动势) 一、动生电动势 = = B S Bll dl v dt = ( ) i d d dl Bll Bl dt dt dt = = = = i Blv 方向可由楞次定律得 到(从 b 指向 a) 二、对动生电动势的解释 由金属电子理论: m e F qv B ev B F qE eE = = − = = − m e F evB F eE = → = → 向下 向上 当 eE evB E vB = = , ,这时, a b v v El − = ,即因 洛仑兹力作用的结果 i = = El lvB 与前面结果完全一致。 ▲ 以上说法与洛仑兹力不作功是否相矛盾呢?不矛盾。以下说明: 总洛仑兹力为: F e v u B = − + ( ) ,它与合成速度 v u + 垂直,不做功。 然而分力, f e v B = − ( ) 对电子做正功,形成动生电动势。而另一分力, F e v u B = − + ( ) , 它沿 −v 方向,做负功。可以证明两功代数和为零,证明如下: F v u + = ( ) 0 总功率为零

F=了+ 代入上式并展开,子下+子+子+子.=0 因为子下=0,”.i=0 fn+了p=0或fi=-立 因此,洛仑兹力作用并不提供能量,而只是传递能量。 补充:导体在恒定磁场中运动时,动生电动势: ab=[(xB).dl 6>0,则。4。 或s=∮,(×B)dl 例题:已知铜棒长L,在匀强磁场B中沿逆 时针方向绕轴以角速度旋转 1、 求铜棒中感生电动势的大小和方向 2、若是半径为L的铜盘绕圆心旋转,求中 心与边缘之间的电势差 解:1、在距0为1处取dl小段,速度v=ol ds,=-Bvdl=-Boldl (下×B)方向为从A->0 各小段的ds,的指向都是一样的, ∴e=-Bol=-BaL 5,的指向是从A到0的 :.Uo-U=BoL 另解:计算铜棒在单位时间所切割的磁感应线数来计算动生电动势 设△r内转过△0角度, AΦ=B.1L-LA8=1B 2、若是铜盘,可以看成是无数根并联的铜棒组成,结果同上。 例题:[程守诛普通物理学第四版p220.14 31如图, 1 )质量为M,长度为1的金属 棒b从静止开始沿倾斜的绝缘框架下滑,设磁场B竖直向上,求棒内的动生时势与时 间的函数关系,忽略摩擦。(2)如果金属棒b是沿光滑的金属框架下滑,结果有何不
F f f = + 代入上式并展开, f v f u f v f u + + + = 0 因为 f v f u = = 0, 0 f u f v + = 0 或 f u f v = − 因此,洛仑兹力作用并不提供能量,而只是传递能量。 补充:导体在恒定磁场中运动时,动生电动势: ( ) b ab a = v B dl 0, ab b u 则ua ; 0, ab b u 则ua 或 ( ) L = v B dl 例题:已知铜棒长 L,在匀强磁场 B 中沿逆 时针方向绕轴以角速度 旋转。 1、求铜棒中感生电动势的大小和方向 2、若是半径为 L 的铜盘绕圆心旋转,求中 心与边缘之间的电势差 解:1、在距 O 为 l 处取 dl 小段,速度 v =l , d Bvdl B ldl i = − = − , (v B) 方向为从 A->O 各小段的 d i 的指向都是一样的, 2 0 2 1 B ldl B L l i = − = − i 的指向是从 A 到 O 的 2 2 1 UO −U A = BL 另解:计算铜棒在单位时间所切割的磁感应线数来计算动生电动势。 设 t 内转过 角度, 2 2 1 2 1 = B L L = BL 2、若是铜盘,可以看成是无数根并联的铜棒组成,结果同上。 例题:[程守洙 普通物理学第四版 p220.14-13]如图,(1)质量为 M,长度为 l 的金属 棒 ab 从静止开始沿倾斜的绝缘框架下滑,设磁场 B 竖直向上,求棒内的动生时势与时 间的函数关系,忽略摩擦。(2)如果金属棒 ab 是沿光滑的金属框架下滑,结果有何不
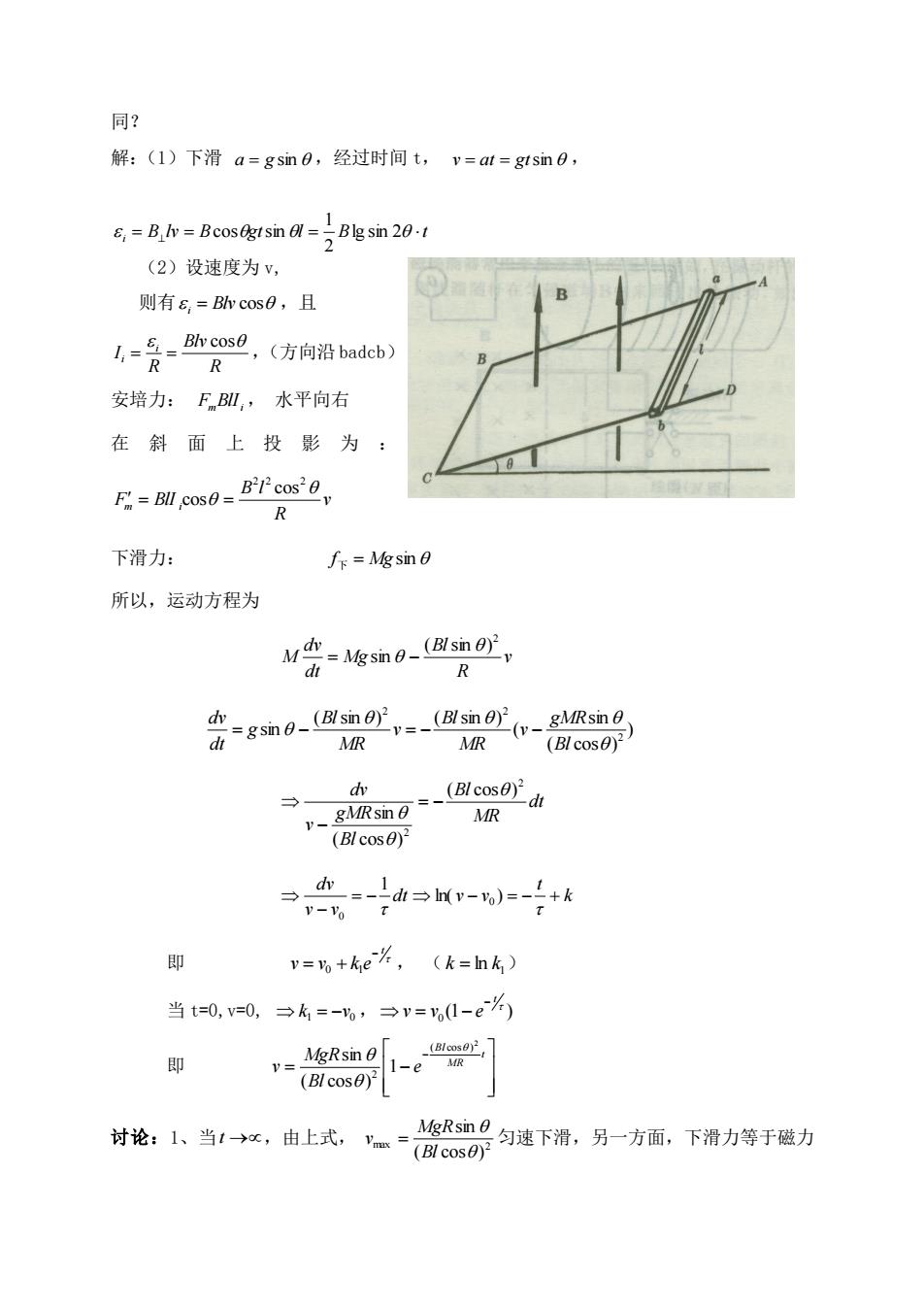
同? 解:(1)下滑a=gsin0,经过时间t,v=at=gtsin0 Bcosrn (2)设速度为v, 则有G,=B弥cos8,且 -是-卧9,(方向沿b) R 安培力:FB即,水平向右 在斜面上投影为: B c0s0 cos 0 R 下滑力: f:=Mgsin 0 所以,运动方程为 M密峻s如0圆阳, R -(v gMRsin MR MR (Bl cos0) (c 小 R v=肠+ke片,(k=nk) 当t=0,=0,→k=-,→v=w1-e%) 即 MgRsin 0 v=(Bicos0) 1-e R 时论:1、当,由上式一匀下滑,另一方,下滑力等于装力
同? 解:(1)下滑 a = g sin ,经过时间 t, v = at = gtsin , B lv B gt l B t i = = = ⊥ lg sin 2 2 1 cos sin (2)设速度为 v, 则有 i = Blv cos ,且 R Blv R I i i cos = = ,(方向沿 badcb) 安培力: FmBlIi , 水平向右 在 斜 面 上 投 影 为 : v R B l F BlI m i 2 2 2 cos = cos = 下滑力: f下 = Mg sin 所以,运动方程为 v R Bl Mg dt dv M 2 ( sin ) sin = − ) ( cos ) sin ( ( sin ) ( sin ) sin 2 2 2 Bl gMR v MR Bl v MR Bl g dt dv = − = − − dt MR Bl Bl gMR v dv 2 2 ( cos ) ( cos ) sin = − − k t dt v v v v dv = − − = − + − ln( ) 1 0 0 即 t v v k e − = 0 + 1 , ( 1 k = ln k ) 当 t=0,v=0, 1 0 k = −v , (1 ) 0 t v v e − = − 即 = − − t MR Bl e Bl MgR v 2 ( cos ) 2 1 ( cos ) sin 讨论:1、当 t → ,由上式, max 2 ( cos ) sin Bl MgR v = 匀速下滑,另一方面,下滑力等于磁力

在斜面上的分力: 即 R 2、达到v以后,势能的减小等于焦耳热 R (BI cos0)2 AE,-Mgh=Mgs.sin 0-Mgvisin0-M'g'Rsn (BI cos0)2 例题:[程守诛普通物理学第五版,p339,13-4]如图,已知1,1,aV,求:金属棒AB 中的动生电动势。 解:同上 B=会 6-编 告r 6的指向是从B到A,也就是A点的电势比B点高,即 d u-w,=会 例题:两个共轴圆线圈,半径分别为R及r(r很小,可认 为小线圈所在的磁场为均匀的),匝数分别为N,和N,大线圈中通有电流1,求当小线 圈沿轴线方向以速度ⅴ运动(两线圈平面保持平行),两者相距为x时,小线圈中心电 动势大小。 秀 B=色RN 2(R2+x33 中=NNmR1 2(R2+x2)3 2 d(R2+x2)
在斜面上的分力。 即 max 2 ( cos ) sin v R Bl Mg Fm = = , max 2 max ( cos ) sin v Bl MgR v = = 2、达到 max v 以后,势能的减小等于焦耳热 2 2 2 2 2 2 ( cos ) ( cos ) sin Bl M g R t R Blv t R Q i = = = t Bl M g R E Mgh Mgs Mgvt p 2 2 2 2 ( cos ) sin sin sin = = = = 例题:[程守洙 普通物理学第五版,p339,13-4]如图,已知 I,l,a v,求:金属棒 AB 中的动生电动势。 解:同上 x I B 2 0 = , vdv x I d Bvdx i 2 = = vdx x I d a l a i i + = = 2 0 ln( ) 2 0 a a l v I + = i 的指向是从 B 到 A,也就是 A 点的电势比 B 点高,即 ln( ) 2 0 a a l v I UA UB + − = 例题:两个共轴圆线圈,半径分别为 R 及 r(r 很小,可认 为小线圈所在的磁场为均匀的),匝数分别为 N1 和 N2 ,大线圈中通有电流 I,求当小线 圈沿轴线方向以速度 v 运动(两线圈平面保持平行),两者相距为 x 时,小线圈中心电 动势大小。 解: 2 3 2 2 1 2 0 ( ) 2 R x R IN B + = 2 3 2 2 2 2 0 1 2 ( ) 2 R x N N r R I + = + = − = − 2 3 2 2 2 2 0 1 2 ( ) 1 2 R x dt d R I N N r dt d

e 2 =3π4NN,r2R21xw (R+x2)3 方向不宜判断 §13-4惑生电动势涡旋电场涡旋电流 一、涡旋电场 动生电动势的非静电力是洛仑兹力,那么磁场变化产生的感生电动势,其非静电力 是什么呢?麦克斯韦认为:即使不存在导体回路,变化的磁场在其周围也会激发一种电 场,叫做感应电场,或涡旋电场。 涡旋电场与静电场比较: 相同处:都对电荷有作用力 不同处:1、涡旋电场是由变化的磁场激发的 2、描述涡旋电场的电力线是闭合的,它是非保守场,即E·d≠0, 而产生感生电动势的非静电力正是这一涡旋电场E, 写f,i-”o与.L有关 在一般情形下,空间E=正。+正,其中。·山=0,所以 6=fEa'di=f En+Eabdi=fE-di 而 =”s打曾 一.=-小曾由电磁学的基本方程之 对于稳恒条件下, 曾=0源=0 →∫E·di=0即静电场的环路定理 所以基本方程是静电场的环路定理,在非稳恒条件下的推广。 [程守洙普通物理学第五版,p348,13-6] 二、涡旋电流(傅科电流Foucault)
2 3 2 2 2 2 0 1 2 ( ) 2 ) 2 3 ( 2 R x x v R I N N r + = − − 2 3 2 2 2 2 0 1 2 ( ) 2 3 R x N N r R I xv + = 方向不宜判断 §13-4 感生电动势 涡旋电场 涡旋电流 一、涡旋电场 动生电动势的非静电力是洛仑兹力,那么磁场变化产生的感生电动势,其非静电力 是什么呢?麦克斯韦认为:即使不存在导体回路,变化的磁场在其周围也会激发一种电 场,叫做感应电场,或涡旋电场。 涡旋电场与静电场比较: 相同处:都对电荷有作用力 不同处:1、涡旋电场是由变化的磁场激发的 2、描述涡旋电场的电力线是闭合的,它是非保守场,即 0 L E dl 涡 , 而产生感生电动势的非静电力正是这一涡旋电场 E涡 , dt d E dl L i = = − 涡 , 与 B 、L 有关 在一般情形下,空间 E E静 E涡 = + , 其中 = 0 L E dl 静 ,所以 E dl E E dl E dl L L L i = = + = 涡 静 涡 , 而 = − ===== − = − ( ) (s) L s i ds t B B ds dt d dt d 当 不变时 ds t B E dl s L = − ( ) 电磁学的基本方程之一 对于稳恒条件下, = 0 dt d 或 = 0 t B = 0 E dl L 即静电场的环路定理 所以基本方程是静电场的环路定理,在非稳恒条件下的推广。 [程守洙 普通物理学第五版,p348,13-6] 二、涡旋电流(傅科电流 Foucault)

1、p204,14-11 R很小,I可以很大, 因为,专x曾。(外加交流电) I@,P=IR 所以Pxo2,当o高到几百几千z时,P可以很大。 2、真空技术上,加热,放出残存在金属面上的少许气体 3、变压器、电机 4、涡电流产生阻尼作用 §13-6自感应 自感应:由于回路中电流产生的磁通量发生变化,而在自身回路中激发感应电动势 的现象,称为自感现象,相应的电动势称为自感电动势。 设回路电流为1,回路几何形状不变,且空间没有铁磁性物质时,则ΦcI,写成 等式, ΦxLI (1) 其中L称为该回路的自感系数(简称自感或电感),单位:享利H,L取决于回路几 何形状以及周围磁介质的磁导率。 当=1时,L=中,可见L在量值上等于当I=1时的中。 由法拉第定律 d 若回路几何形状和周围磁导率都不变,即L不变 出-0,气=-1出(关于负号的解释与力学的惯性比镜) 若回路有N匝的线圈组,某匝的磁通量为中,则 +D2+.+Φx=LI,即 y=L1,y=④,+①2+.+④、为全磁通 若中,=2=.=中w=,则N@=Ll (当I=1,L=w,或L=NΦ)
1、p204,14-11 R 很小,I 可以很大, 因为, dt d i (外加交流电) I i , P I i R 2 = 所以 2 P ,当 高到几百几千 Hz 时,P 可以很大。 2、真空技术上,加热,放出残存在金属面上的少许气体 3、变压器、电机 4、涡电流产生阻尼作用 §13-6 自感应 自感应:由于回路中电流产生的磁通量发生变化,而在自身回路中激发感应电动势 的现象,称为自感现象,相应的电动势称为自感电动势。 设回路电流为 I,回路几何形状不变,且空间没有铁磁性物质时,则 I ,写成 等式, LI (1) 其中 L 称为该回路的自感系数(简称自感或电感),单位:享利 H,L 取决于回路几 何形状以及周围磁介质的磁导率。 当 I=1 时, L = ,可见 L 在量值上等于当 I=1 时的 。 由法拉第定律 ( ) ( ) dt dL I dt dI g L dt d LI dt d L = − = + − 若回路几何形状和周围磁导率都不变,即 L 不变 = 0 dt dL , dt dI L = −L (关于负号的解释与力学的惯性比较) 若回路有 N 匝的线圈组,某匝的磁通量为 i ,则 LI 1 + 2 ++ N = ,即 = LI , = 1 + 2 ++ N 为全磁通 若 1 = 2 == N = ,则 N = LI (当 I=1, L = ,或 L = N )

当回路不形变,周国磁介质不变,仍有=一出 L是N匝线圈的自感系数, (2 注意(1)与(2)式的区别。 例题:[P209,14-2]求长直螺线管L? 解:己知L、R、N、4 因为B=,=空 ,按定义,N=L ,又 所以, L=LV 补充例题:[五版,p357,13-7] 设有一电缆,由两个“无限长”的同轴的 圆筒状的导体组成,其间充满磁导率为μ的础 介质,电缆中沿内圆筒和外圆筒流过的电流 大小相等,求电缆单位长度的自感系数。 解:应用安培环路定律,可知在内圆筒之内和 外圆筒之外的空间中的磁感应强度都为零,在 内外两圆筒之间,离开轴线距离为r处的磁感 应强度为 B-,(R≤r≤R) 考虑长为1的部分电缆,通过面积元仙的磁通量为 d=B.ldr=uull dr 2πr 所以两圆筒之间(1长的一段)的总磁通量为
当回路不形变,周围磁介质不变,仍有 dt dI L = −L L 是 N 匝线圈的自感系数, dt dI L L = − (2) 注意(1)与(2)式的区别。 例题:[P209,14-2] 求长直螺线管 L? 解:已知 L、R、N、 因为 l NI B = , l IN S N 2 = ,按定义, N = LI l R N l N S I N L 2 2 2 = = = ,又 l N n = , Sl =V , 所以, L n V 2 = 补充例题:[五版,p357,13-7] 设有一电缆,由两个“无限长”的同轴的 圆筒状的导体组成,其间充满磁导率为 的磁 介质,电缆中沿内圆筒和外圆筒流过的电流 I 大小相等,求电缆单位长度的自感系数。 解:应用安培环路定律,可知在内圆筒之内和 外圆筒之外的空间中的磁感应强度都为零,在 内外两圆筒之间,离开轴线距离为 r 处的磁感 应强度为 r I B 2 = ,( 1 R2 R r ) 考虑长为 l 的部分电缆,通过面积元 ldr 的磁通量为 r Il dr d B ldr 2 = = 所以两圆筒之间(l 长的一段)的总磁通量为
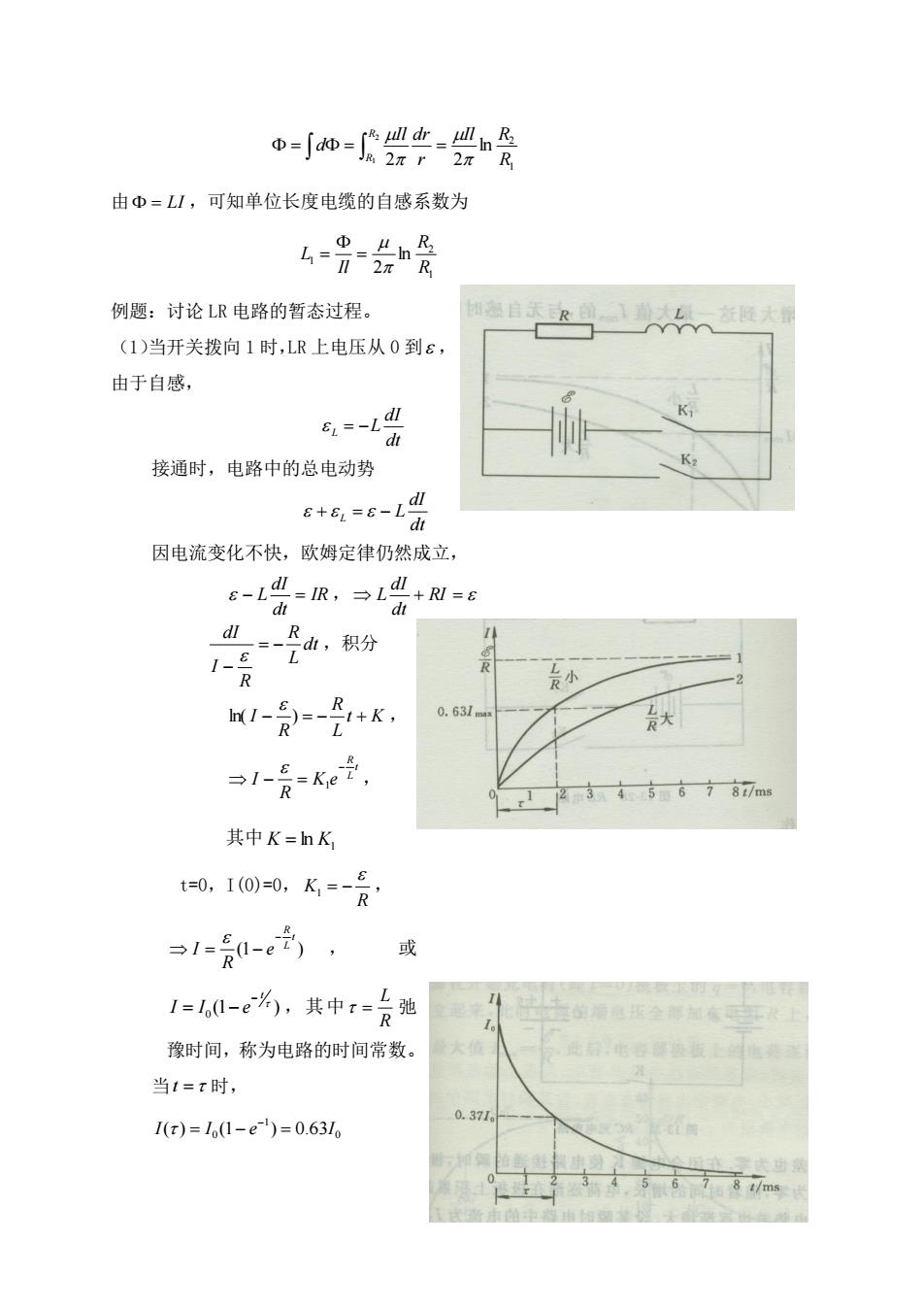
=-中尝是 由中=L1,可知单位长度电缆的自感系数为 49会是 例题:讨论LR电路的暂态过程。 (1)当开关拨向1时,LR上电压从0到ε, 由于自感, 接通时,电路中的总电动势 6+=8-l出 因电流变化不快,欧姆定律仍然成立, 6 小 1-员-是, 0.631m 大 31食=水e之, ,1246787m 其中K=hK 0.10=0.K=-员 1=l-e色, 或 1=60-%,其中=克驰 豫时间,称为电路的时间常数。 当t=x时, 1(x)=11-e)=0.631 8 t/ms
1 2 ln 2 2 2 1 R Il R r Il dr d R R = = = 由 = LI ,可知单位长度电缆的自感系数为 1 2 1 ln 2 R R Il L = = 例题:讨论 LR 电路的暂态过程。 (1)当开关拨向 1 时,LR 上电压从 0 到 , 由于自感, dt dI L = −L 接通时,电路中的总电动势 dt dI + L = − L 因电流变化不快,欧姆定律仍然成立, IR dt dI − L = , + RI = dt dI L dt L R R I dI = − − ,积分 t K L R R ln( I − ) = − + , t L R K e R I − − = 1 , 其中 1 K = ln K t=0,I(0)=0, R K 1 = − , (1 ) t L R e R I − = − , 或 (1 ) 0 t I I e − = − ,其中 R L = 弛 豫时间,称为电路的时间常数。 当 t = 时, 0 1 I( ) = I 0 (1− e ) = 0.63I −