
目录 能级与光谱模块 弗兰克一赫兹实验.1 费米-狄拉克分布.4 用多功能光栅光谱仪进行钠光谱测量实验.9 场致效应模块 塞曼效应15 电子自旋共振. 20 波特性模块 声速测定. .26 噪声频谐分析实验 32 微波技术实验 6 相对论与核物理模块 验证快速电子的动量与动能的相对论关系 .53 CT实验. .61 固体特性模块 超导转变温度与磁悬浮力测量实验. 65 色度实验 72 传感器实验 粉末X-射线衍射仪的使用.87
目 录 能级与光谱模块 弗兰克—赫兹实验 . 1 费米-狄拉克分布 . 4 用多功能光栅光谱仪进行钠光谱测量实验 . 9 场致效应模块 塞曼效应 . 15 电子自旋共振 . 20 波特性模块 声速测定 . 26 噪声频谱分析实验 . 32 微波技术实验 . 46 相对论与核物理模块 验证快速电子的动量与动能的相对论关系 . 53 CT实验 . 61 固体特性模块 超导转变温度与磁悬浮力测量实验 . 65 色度实验 . 72 传感器实验 . 83 粉末X-射线衍射仪的使用 . 87

弗兰克一赫兹实验 弗兰克-赫兹实验是1914年由德国物理学家弗兰克和赫兹设计完成的。该实验研究电子与原子碰 撞前后能量的变化,能观测到汞原子的激发电势和电离电势,可以证明原子能级的存在,为波尔的原 子结构理论假说提供有力的实验证据。该实验的方法至今仍是探索原子结构的重要手段之一。 1913年丹麦物理学家玻尔(NBor)提出了原子能级的概念并建立了原子模型理论。该理论指出, 原子处于稳定状态时不辐射能量,当原子从高能态(能量£)向低能态(能量E)跃迁时才辐射。辐射 能最满足 AE E-E (1) 对于外界提供的能量,只有满足原子跃迁到高能级的能级差,原子才吸收并跃迁,否则不吸收。 1914年德国物理学家弗兰克(J-Franck)和赫兹 (G-Hertz)用慢电子穿过汞蒸气的实验,测定了汞原子的第 微电流仪 微发电位,从而证明了原子分立能态的存在。后来他们叉 观测了实验中被激发的原子回到正常态时所辐射的光,测出 电子 的辐射光的频率很好地满足了玻尔理论。弗兰克一赫兹实验 的结果为玻尔理论提供了直接证据。玻尔因其原子模型理论 获1922年诺贝尔物理学奖,而弗兰克与赫兹的实验也于1925 年获此奖。 【实验目的】 1、了解弗兰克-赫兹实验仪的结构、原理,学会它的调 灯电压 节和使用方法。 图1弗兰克赫兹实验原理图 2、了解电子与原子之间的弹性碰撞和非弹性碰撞。 3、测量氩原子的第一激发电位: 4、证实原子能级的存在,加深对原子结构的了解: 【预习思考题】 1.简述F一H实验管原理。 2.为什么I一V曲线呈周期性变化? 3.为什么实验中板极电流并不是突然下降,在极大值附近出现的“峰”总会有一定的宽度?为什么板 极电流并没有降到零? 4.能否采用适当的管子和线路,在较低的温度下就有可能进行高能级激发电位或电离电位的测定? 【实验器材】 智能型弗兰克-赫兹实验仪,计算机,示波器 1
弗兰克—赫兹实验 弗兰克-赫兹实验是 1914 年由德国物理学家弗兰克和赫兹设计完成的。该实验研究电子与原子碰 撞前后能量的变化,能观测到汞原子的激发电势和电离电势,可以证明原子能级的存在,为波尔的原 子结构理论假说提供有力的实验证据。该实验的方法至今仍是探索原子结构的重要手段之一。 1913 年丹麦物理学家玻尔(NwBohr)提出了原子能级的概念并建立了原子模型理论。该理论指出, 原子处于稳定状态时不辐射能量,当原子从高能态(能量Em)向低能态(能量En)跃迁时才辐射。辐射 能量满足 ΔE = Em−En (1) 对于外界提供的能量,只有满足原子跃迁到高能级的能级差,原子才吸收并跃迁,否则不吸收。 1914 年德国物理学家弗兰克( JwFranck)和赫兹 (GwHertz)用慢电子穿过汞蒸气的实验,测定了汞原子的第 一激发电位,从而证明了原子分立能态的存在。后来他们又 观测了实验中被激发的原子回到正常态时所辐射的光,测出 的辐射光的频率很好地满足了玻尔理论。弗兰克—赫兹实验 的结果为玻尔理论提供了直接证据。玻尔因其原子模型理论 获 1922年诺贝尔物理学奖,而弗兰克与赫兹的实验也于 1925 年获此奖。 【实验目的】 1、了解弗兰克-赫兹实验仪的结构、原理,学会它的调 节和使用方法。 2、了解电子与原子之间的弹性碰撞和非弹性碰撞。 3、测量氩原子的第一激发电位; 4、证实原子能级的存在,加深对原子结构的了解; 【预习思考题】 1. 简述 F—H 实验管原理。 2. 为什么 I—V 曲线呈周期性变化? 3. 为什么实验中板极电流并不是突然下降,在极大值附近出现的“峰”总会有一定的宽度?为什么板 极电流并没有降到零? 4. 能否采用适当的管子和线路,在较低的温度下就有可能进行高能级激发电位或电离电位的测定? 【实验器材】 智能型弗兰克-赫兹实验仪,计算机,示波器 图 1 弗兰克-赫兹实验原理图 电子 氩原子 G2 G1 A I UG2K UG2A 微电流仪 K UG1K 灯丝电压 1

【实验原理】 夫兰克一赫兹实验原理如图1所示,在真空管中充待测氩气,阴极K,阳极A,G、G分别为第一、 第二栅极。 K-GG:加正向电压,为电子提供能量。Ucx的作用主要是消除空间电荷对阴极电子发射的影响 提高发射效率。G-A加反向电压,形成拒斥电场。 电子从K发出,在K-G区间获得能量,在G一A区间损失能量。如果电子进入G一A区域时动能大于或 等于Uc,A,就能到达阳极形成阳极电流 电子在不同区间的情况: 1,K-G区间电子迅速被电场加速而获得能量。 2.G-G区间电子与氩原子碰撞。当其能量小于氩原子第一激发态与基态的能级差4E-&-B时, 氩原子基本不吸收电子的能量,碰撞属于弹性碰撞。当电子的能量达到4,则可能在碰撞中被氩原子 吸收这部分能量,这时的碰撞属于非弹性碰撞。4称为临界能量。 3.GA区间电子受阻,被拒斥电场吸收能量。若电子进入此区间时的能量小于则不能达到 阳极。 由此可见,若ex(4E,则电子带着e6ax的能量进 /(nA) 入G-A区域。随者✉的增加,电流增加(如图2中 a段)。 若ex=4测电子在达到G,处刚够临界能量,不 过它立即开始消耗能量了,继续增大x,电子能最被 吸收的概率逐渐增加,阳极电电电流逐渐下降(如图 Uex(V) 2中ab殿)。 继续增大,电子碰撞后的剩余能量也增加,到 图2弗兰克赫兹实验U6x~1曲线 达阳极的电子又会逐渐增多(如图2中bc段)。 若el6x>n4E,则电子在进入G2-A区域之前可能次被氩原子碰撞而损失能量。阳极电流随加速电压 U。K变化曲线就形成个峰值,如图2所示。相邻峰值之间的电压差4称为氩原子的第一激发电位。 氯原子第一激发态与基态间的能级差 (2) 【实验内容及步骤】 测量原子的第一激发电位。通过一I曲线,观察原子能量量子化情况,并求出氩原子的第一激 发电位。 一、实验步骤 1.将面板上的四对插座(灯丝电压,Uk:第二栅压,UGK:第一栅压,UGA:拒斥电压)按面 板上的接线图与电子管测试架上的相应插座用专用连接线连好。将实验仪器与计算机(或示波器)连 接好
【实验原理】 夫兰克一赫兹实验原理如图 1 所示,在真空管中充待测氩气,阴极K,阳极A,G1 、G2分别为第一、 第二栅极。 K-G1-G2加正向电压,为电子提供能量。 的作用主要是消除空间电荷对阴极电子发射的影响, 提高发射效率。G G K1 U 2-A加反向电压,形成拒斥电场。 电子从K发出,在K-G2区间获得能量,在G2-A区间损失能量。如果电子进入G2-A区域时动能大于或 等于e ,就能到达阳极形成阳极电流I. G A2 U 电子在不同区间的情况: 1. K-G1区间 电子迅速被电场加速而获得能量。 2. G1-G2区间 电子与氩原子碰撞。当其能量小于氩原子第一激发态与基态的能级差ΔE=E2−E1 时, 氩原子基本不吸收电子的能量,碰撞属于弹性碰撞。当电子的能量达到ΔE,则可能在碰撞中被氩原子 吸收这部分能量,这时的碰撞属于非弹性碰撞。ΔE称为临界能量。 3. G2-A区间 电子受阻,被拒斥电场吸收能量。若电子进入此区间时的能量小于eU G2A则不能达到 阳极。 图 2 弗兰克-赫兹实验 G K2 U ~I 曲线 a b c I(nA) G K2 U (V ) O U1 U2 U3 U4 U5 U6 U7 由此可见,若eUG2KnΔE,则电子在进入G2-A区域之前可能n次被氩原子碰撞而损失能量。阳极电流I随加速电压 变化曲线就形成n个峰值,如图 2 所示。相邻峰值之间的电压差ΔU称为氩原子的第一激发电位。 氩原子第一激发态与基态间的能级差 G K2 U ΔE= eΔU (2) 【实验内容及步骤】 测量原子的第一激发电位。通过UG2K-I曲线,观察原子能量量子化情况,并求出氩原子的第一激 发电位。 一、实验步骤 1.将面板上的四对插座(灯丝电压, :第二栅压, :第一栅压, :拒斥电压)按面 板上的接线图与电子管测试架上的相应插座用专用连接线连好。将实验仪器与计算机(或示波器)连 接好。 G K2 U G K1 U G A2 U 2

2.打开仪器电源,开启计算机(成示波器)。 3。“自动/手动”挡开机时位于“手动”位置,此时“手动”灯点亮。 4.电流档为10A、10A、10'A和10A、开机时位于“10A”本实验保持此档不变。 5.按电子管测试架铭牌上给出的灯丝电压值、第一懦压Uk、拒斥电压心、电流量程预置相应 值。按下相应电压键,指示灯点亮,按下“A”健或“V”键,更改预置值,若按下“” 键,可更改预置值的位数,向前或向后移动一位。 6。电子管的加载。同时按下“st”键和“)”健,则灯丝电压,第一栅压,第二栅压和拒斥电压等 四组电压按预置值加载到电子管上,此时“加载”指示灯亮。注意:只有四组电压都加载时,此灯才 常亮。 7.四组电压都加载后,预热十分钟以上方可进行实验, 8.按下“自动/手动”链,此时“自动”灯点亮。此时仪器进入自动测量状态。 9.在自动测量状态下,第二栅压从0开始变到85V结束,期间要注意观察示波器曲线峰值位置,并记 录相应的第二栅压值。 10.自动状态测量结束后,按“自动/手动”健到“手动”状态,等待5分钟后进行手动测量。 11.改变第二栅压从0开始变到85V结束,要求每改变1V记录相应I和Uc.k值。 12.实验完毕后,同时按下“set”键+“<”健,“加载”指示灯熄灭,使四组电压卸载。 13.关闭仪器电源。 二、数据处理 1.作出r尚线,确定出极大时所对应的电压Ux 2.用最小二乘法求氩的第一激发电位,并计算不确定度 【注意事项】 灯丝电压和加速电压过大会导致电子管电离,电子管电离后电子管电流会自发增大直至烧毁。 旦发现I为负值或正值超过10μA,迅速关机,5分钟后重新开机。 【思考题】 1.一I曲线电流下降并不十分陡峭,主要原因是什么? 2.I的谷值并不为零,而且谷值依次沿Ux轴升高,如何解释? 3.第一峰值所对应的电压是否等于第一激发电位?原因是什么? 4.写出氩原子第一激发态与基态的能级差。 3
2.打开仪器电源,开启计算机(或示波器)。 3.“自动/手动”挡开机时位于“手动”位置,此时“手动 ”灯点亮。 4.电流档为 10−9 A、10−8 A、10−7 A和 10−6 A、开机时位于“10−9 A”本实验保持此档不变。 5.按电子管测试架铭牌上给出的灯丝电压值、第一栅压 G K1 U 、拒斥电压 、电流量程I预置相应 值。按下相应电压键,指示灯点亮,按下“∧”键或“∨”键,更改预置值,若按下“” 键,可更改预置值的位数,向前或向后移动一位。 G A2 U 6.电子管的加载。同时按下“set” 键和“>” 键,则灯丝电压,第一栅压,第二栅压和拒斥电压等 四组电压按预置值加载到电子管上,此时“加载 ”指示灯亮。注意:只有四组电压都加载时,此灯才 常亮。 7.四组电压都加载后,预热十分钟以上方可进行实验。 8.按下“自动/手动”键,此时“自动 ”灯点亮。此时仪器进入自动测量状态。 9.在自动测量状态下,第二栅压从 0 开始变到 85V 结束,期间要注意观察示波器曲线峰值位置,并记 录相应的第二栅压值。 10.自动状态测量结束后,按“自动/手动”键到“手动”状态,等待 5 分钟后进行手动测量。 11.改变第二栅压从 0 开始变到 85V 结束,要求每改变 1V 记录相应 I 和 值。 G K2 U 12.实验完毕后,同时按下“set ”键 +“< ”键,“加载 ”指示灯熄灭,使四组电压卸载。 13.关闭仪器电源。 二、数据处理 1.作出UG2K-I曲线,确定出I极大时所对应的电压 . G K2 U 2.用最小二乘法求氩的第一激发电位,并计算不确定度。 【注意事项】 灯丝电压和加速电压过大会导致电子管电离,电子管电离后电子管电流会自发增大直至烧毁。一 旦发现 I 为负值或正值超过 10μA,迅速关机,5 分钟后重新开机。 【思考题】 1. UG2K-I曲线电流下降并不十分陡峭,主要原因是什么? 2.I 的谷值并不为零,而且谷值依次沿 轴升高,如何解释? G K2 U 3.第一峰值所对应的电压是否等于第一激发电位?原因是什么? 4.写出氩原子第一激发态与基态的能级差。 3
费米-狄拉克分布 【实验目的】 1.通过实验验证费米一狄拉克分布 2.学习一种实验方法及处理实验数据的技巧, 【实验器材】 FWⅡ型费米-狄拉克分布实验仪 【预习思考题】 1.金属中的电子按能量的分布遵从什么规律?表现出什么特性? 2。由于金属内部电子的能量无法测量,本实验中具体是如何进行测量的? 3。电子作圆周运动的半径由什么决定,它对阳极电流又有什么影响? 【实验原理】 近代电子理论认为金属中的电子按能量的分布是遵从费米一狄拉克的量子统计规律的,费米分布 函数为 (e)-expl(-)/KT]1 (1) 金属中的每个电子都占有一定能量的能级,这些能级相互靠得很近,形成能带。当其温度为绝对 零度时,金属中电子的平均能量并不为零。此时金属中的电子将能量从零到能量£,(6,称费米能级, 6,的值随金属的不同而不同)的能级全部占据。而高于费米能级的那些能级全部空着,没有电子去占 据。如图(1)中的实线所示,当金属的温度为1500℃,则靠近费米能级的少数电子由于运动的加剧, 其能量超过6值,因而从低于费米能级的能带跃迁到高于费米能级的能带上去,其分布曲线如图(1) 中虚线所示。我们的实验是在灯丝灼热(约1400℃~1500℃)的情况下进行的,因此我们实验所测的 结果也只是靠近费米能级的一部分,如图(1)中矩形所包的虚线部分。 对D式求号可得8e)-2e-网 (2) (1)、(2)两式的理论曲线如图(1)和图(2)所示。 g(E) 4 图1, 4
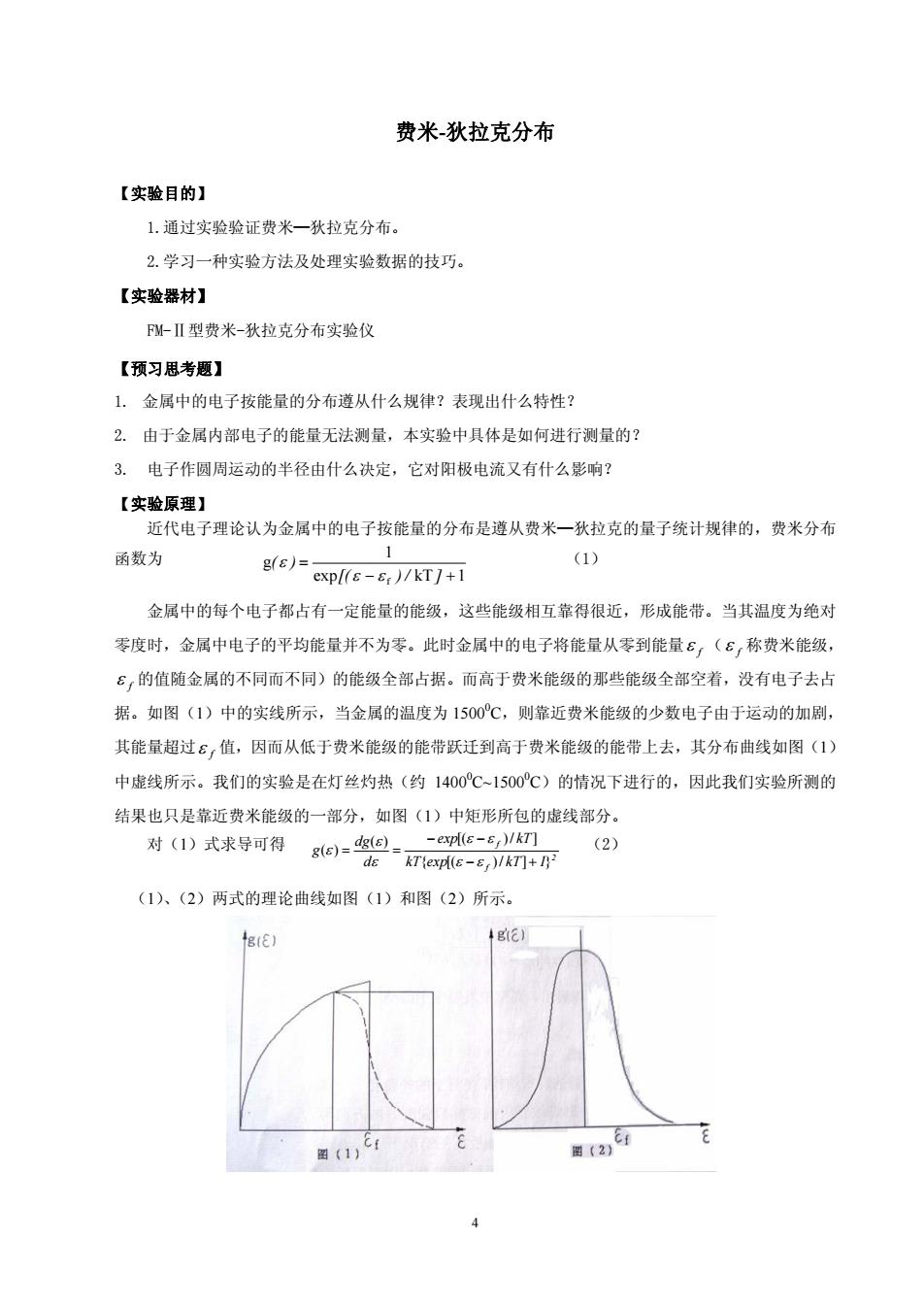
费米-狄拉克分布 【实验目的】 1.通过实验验证费米—狄拉克分布。 2.学习一种实验方法及处理实验数据的技巧。 【实验器材】 FM-Ⅱ型费米-狄拉克分布实验仪 【预习思考题】 1. 金属中的电子按能量的分布遵从什么规律?表现出什么特性? 2. 由于金属内部电子的能量无法测量,本实验中具体是如何进行测量的? 3. 电子作圆周运动的半径由什么决定,它对阳极电流又有什么影响? 【实验原理】 近代电子理论认为金属中的电子按能量的分布是遵从费米—狄拉克的量子统计规律的,费米分布 函数为 exp 1kT 1 g − f + = ]/)[( )( εε ε (1) 金属中的每个电子都占有一定能量的能级,这些能级相互靠得很近,形成能带。当其温度为绝对 零度时,金属中电子的平均能量并不为零。此时金属中的电子将能量从零到能量 f ε ( f ε 称费米能级, f ε 的值随金属的不同而不同)的能级全部占据。而高于费米能级的那些能级全部空着,没有电子去占 据。如图(1)中的实线所示,当金属的温度为 15000 C,则靠近费米能级的少数电子由于运动的加剧, 其能量超过 f ε 值,因而从低于费米能级的能带跃迁到高于费米能级的能带上去,其分布曲线如图(1) 中虚线所示。我们的实验是在灯丝灼热(约 14000 C~15000 C)的情况下进行的,因此我们实验所测的 结果也只是靠近费米能级的一部分,如图(1)中矩形所包的虚线部分。 对(1)式求导可得 2 f f expkT 1kT exp kT d dg g }]/)[({ )( ]/)[( )( +− − − == εε ε ε ε ε ε (2) (1)、(2)两式的理论曲线如图(1)和图(2)所示。 4

由于金属内部电子的能量无法测量,只能对真空中热发射电子的动能分布进行测量。由于电子在 真空中的热运动与电子在金属内部的运动情况完全不同,这是因为金属内部存在者带正电的原子核, 电子不但有热运动的动能,而且还具有势能,真空中的电子就不存在势能,6=0,还要消耗一部分能 量用作逸出功,因此从金属内部电子的能量£减去逸出功A,就可得到真空中热发射电子的动能£ Ek=E-A (3) 此外,在真空与金属表面附近还存在着电子气形成的偶电层,就是说逃出金属表面的电子,还要 消耗一些能量穿越偶电层,根据前苏联科学院院士,符伦克尔和塔姆的理论,电子穿越偶电层所需要 的能量,也就是该金属的费米能级£,·考虑到这两个因素之后对费米函数作适当的修正是非常必要的 修正后的费米函数应为: 8(6)=exp( (4) 对(4)式求导得 8)-se -expl(E -E)/KT] (5) dsk灯epls-e)/kT+1 由(4)、(5)两式可以看出,真空中发射电子的动能分布也遵从费米一狄拉克分布。 【实验方法及数据处理】 本实验是利用理想二极管的特殊结构,在管子的外面套一个螺线管,并且通以直流电流,则螺线 管中的磁感应强度B的方向与光子的轴线(灯丝)平行,在二极管不加板压的情况下(“。=0),从 灯丝发射出电子,沿半径方向飞向圆柱面板级(阳极),由于阳板电压为零,所以电子在不受外电场力 的作用下,保持其初动能飞向阳极形成阳极饱和电流,其线路如图(3)所示
由于金属内部电子的能量无法测量,只能对真空中热发射电子的动能分布进行测量。由于电子在 真空中的热运动与电子在金属内部的运动情况完全不同,这是因为金属内部存在着带正电的原子核, 电子不但有热运动的动能,而且还具有势能,真空中的电子就不存在势能, f ε =0,还要消耗一部分能 量用作逸出功,因此从金属内部电子的能量ε 减去逸出功 A,就可得到真空中热发射电子的动能 k ε ε k ε −= A (3) 此外,在真空与金属表面附近还存在着电子气形成的偶电层,就是说逃出金属表面的电子,还要 消耗一些能量穿越偶电层,根据前苏联科学院院士,符伦克尔和塔姆的理论,电子穿越偶电层所需要 的能量,也就是该金属的费米能级 f ε 。考虑到这两个因素之后对费米函数作适当的修正是非常必要的, 修正后的费米函数应为: exp 1kT 1 g fk k +− = ]/)[( )( εε ε (4) 对(4)式 求导得 2 fk fk k k k expkT 1kT exp kT d dg g }]/)[({ )( ]/)[( )( +− − − == εε ε ε ε ε ε (5) 由(4)、(5)两式可以看出,真空中发射电子的动能分布也遵从费米—狄拉克分布。 【实验方法及数据处理】 本实验是利用理想二极管的特殊结构,在管子的外面套一个螺线管,并且通以直流电流,则螺线 管中的磁感应强度 B 的方向与光子的轴线(灯丝)平行,在二极管不加板压的情况下( p = 0u ),从 灯丝发射出电子,沿半径方向飞向圆柱面板级(阳极),由于阳板电压为零,所以电子在不受外电场力 的作用下,保持其初动能飞向阳极形成阳极饱和电流,其线路如图(3)所示。 5

由于电子的初动能各不相同,如何将它们按相等的动能间隔区分开来,并且求出电子数目的相对 值,便成为本实验的焦点。由图(4)可知,从二极管灯丝(即圆心)发射出的电子,沿半径方向飞向 圆柱面阳极(即圆周),在螺线管所产生的磁感应强度B的作用下,电子将受到洛仑兹力F=-v×B 而作匀速圆周运动。洛仑兹力是向心力,它不改变电子的动能,由于v⊥B,所以洛仑兹力公式可用 下式表示: 五=Ber=m (6) R v=BeR m (7) (7)式中的ⅴ是电子沿二极管半径方向的速度:或者电子的速度在半径方向的分量,R是电子作 匀速圆周运动的半径,m是电子的质量,B是螺线管中间部分的磁感应强度,B的计算公式为: B=4 (8) +D (8)式中,4=4π×I0-?(Wm)是真空中的磁导率:N是螺线管的总匝数:L和D分别是螺线 管的长度和直径,1是通过螺线管的电流强度。将(7)、(8)代入(6)式可得真空中电子的动能为: 2+D:m (9 由(4)可看出,若电子作匀速圆周运动的半径)¢(是圆柱面阳极的直径),电子就能达到阳 极,形成闲极电流,若R(号,电子就不能到达阳极,这一部分电子对闲极电流无贡献。可见电子作匀 速圆周运动的半径(取决于。)直接影响阳极电流的大小,将R=号代入(9)式可得 Ex=KI (10) (10)式中 K=产x10m"wm(S 2(+D m 为一常数,由(I0)式可知真空中发射电子的动能与螺线管中的电流强度的平方成正比,而洛仑 兹力不改变电子的动能,它只影响电子作匀速圆周运动的半径的大小,对动能一定的电子,向心力越 大(即后越大)匀速圆周运动的半径越小,当动能增加△5x时,将有相应数量的电子因其圆周运动的 半径小于号而不能达到阳极,所以阳极电流将减小△山,·又因为△5x与店成正比,所以可用代替 变量6x进行实验及数据处理。 实验中,设灯丝电流强度稳定不变,阳极电压为零,理想二极管的饱和电流为: IP。=n,e (11) (11)式中的m,以及下面的nn2几,.均为单位时间内到达阳极的电子数目,当后以相等的改 6
由于电子的初动能各不相同,如何将它们按相等的动能间隔区分开来,并且求出电子数目的相对 值,便成为本实验的焦点。由图(4)可知,从二极管灯丝(即圆心)发射出的电子,沿半径方向飞向 圆柱面阳极(即圆周),在螺线管所产生的磁感应强度 B 的作用下,电子将受到洛仑兹力 = − × BevF 而作匀速圆周运动。洛仑兹力是向心力,它不改变电子的动能,由于 ⊥ Bv ,所以洛仑兹力公式可用 下式表示: R mv Bevf 2 L == (6) m BeR v = (7) (7)式中的 v 是电子沿二极管半径方向的速度;或者电子的速度在半径方向的分量,R 是电子作 匀速圆周运动的半径,m 是电子的质量,B 是螺线管中间部分的磁感应强度,B 的计算公式为: 22 B0 DL NI B + = μ (8) (8)式中, (H/m)是真空中的磁导率;N是螺线管的总匝数;L和D分别是螺线 管的长度和直径,I 7 0 104 − πμ ×= B是通过螺线管的电流强度。将( B 7)、(8)代入(6)式可得真空中电子的动能为: 2 B 2 22 222 2 0 K I m e DL2 RNm mv 2 1 )( + == μ ε (9) 由(4)可看出,若电子作匀速圆周运动的半径 4 d R〉 (d是圆柱面阳极的直径),电子就能达到阳 极,形成阳极电流,若 4 d R〈 ,电子就不能到达阳极,这一部分电子对阳极电流无贡献。可见电子作匀 速圆周运动的半径(取决于IB)直接影响阳极电流的大小,将 B 4 d R = 代入(9)式可得 (10) 2 K = KI B ε (10)式中 2 22 2 2214 m e DL2 mdN10 K )( + )( × = − π 为一常数,由(10)式可知真空中发射电子的动能与螺线管中的电流强度的平方成正比,而洛仑 兹力不改变电子的动能,它只影响电子作匀速圆周运动的半径的大小,对动能一定的电子,向心力越 大(即 越大)匀速圆周运动的半径越小,当动能增加 2 B I K Δε 时,将有相应数量的电子因其圆周运动的 半径小于 4 d 而不能达到阳极,所以阳极电流将减小 p ΔI ,又因为 K Δε 与 成正比,所以可用 代替 变量 2 B I 2 B I K ε 进行实验及数据处理。 实验中,设灯丝电流强度稳定不变,阳极电压为零,理想二极管的饱和电流为: = 00 enIP (11) (11)式中的 n0 以及下面的 nnn 321 ;;; K均为单位时间内到达阳极的电子数目,当 以相等的改 2 B I 6

变量依次增加下去,我们将得到一组方程: IP =ne 3=n, (12) ,。 由(11)、(12)式联立可得 △P,=P。-P=(m,-n,)e=An,e] △P,=IP-IP,=(n.-n,e=△n,e (13) 2)特 (1 IP IPo n2 no (14) △IP,IIP,=△n,/n △P/IP。=△n,/no (15) 为了配合理论上的要求,操作时事先选好的值,使其等间隔的增加,然后以其平方根的值,作 为实验测景时的电流值,进行实际测试。 【数据记录】 1螺线管的总匝数 N= 2.螺线管的长度 L= m 3.螺线管的平均直径 D= 4.真空中的磁导率 。=4π×10-(H1m) 5.圆柱面极的直径 d-8.4mm(用测量显微镜测) (1)以P/ID,为y轴,以I后为x轴,作g(8x)~6x曲线。 (2)以△P/P,为y轴,以I后为x轴,作g(E)~Ex曲线。 -△2,检查是否满足归一化条件。 3)求∑=B (4)计算g(6)~6x曲线蜂值对应的6值即为£,值。 【分析讨论】 7
变量依次增加下去,我们将得到一组方程: ⎪ ⎭ ⎪ ⎬ ⎫ = = LL enIP enIP 22 11 (12) 由(11)、(12)式联立可得 ⎪ ⎭ ⎪ ⎬ ⎫ Δ=−=−=Δ Δ=−=−=Δ LL enennIPIPIP enennIPIPIP 21212 2 10101 1 )( )( (13) )( )( 11 12 得 (14) ⎪ ⎭ ⎪ ⎬ ⎫ = = LL 0202 0101 nnIPIP nnIPIP // // )( )( 11 13 得 (15) ⎪ ⎭ ⎪ ⎬ ⎫ Δ=Δ Δ=Δ LL 02 02 0101 nnIPIP nnIPIP // // 为了配合理论上的要求,操作时事先选好 的值,使其等间隔的增加,然后以其平方根的值,作 为实验测量时的电流值,进行实际测试。 2 B I 【数据记录】 1.螺线管的总匝数 N= 2.螺线管的长度 L= m 3.螺线管的平均直径 D= m 4.真空中的磁导率 mH104 )/( 7 0 − πμ ×= 5.圆柱面极的直径 d=8.4mm(用测量显微镜测) (1)以 / IPIP 0i 为 y 轴,以 为 x 轴,作 2 B I KK g ε ~)( ε 曲线。 (2)以 为 Δ / IPIP 0i y 轴,以 为 x 轴,作 曲线。 2 B I K K ' g ~)( εε (3)求∑ Δ = 0 i IP IP ,检查是否满足归一化条件。 (4)计算 K K 曲线峰值对应的 ' g ~)( εε K ε 值即为 f ε 值。 【分析讨论】 7

120 080 569.0 066.0 0060 000T 005.0 05.0 620 0260 0650 088.0 5640 06.0 0060 0210 950 0800 520 0600 020 0890 100.0
0.600 0.774 0.560 0.748 0.520 0.721 0.480 0.693 0.440 0.663 0.400 0.632 0.360 0.600 1.000 1.000 % 0.320 0.566 0.960 0.980 E 0.280 0.529 0.920 0.959 0.240 0.490 0.880 0.938 0.200 0.447 0.840 0.916 0.160 0.400 0.800 0.894 0.120 0.346 0.760 0.872 0.080 0.283 0.720 0.848 0.040 0.200 0.680 0.825 0.000 0.000 0.640 0.800 IB 2 IB IPi IPi/ IP0 △IP = IP i i- IPi+1 △IPi/ IP0 IB 2 IB IPi IPi/ IP0 △IP = IP i i- IPi+1 △IPi/ IP0 ∑(△IPi/ IP )0 8

用多功能光栅光谱仪进行钠光谱测量实验 碱金属原子的光谱和氢原子光谱相似,也可以归纳成一些谱线系列,而且各种不同的碱金属原子具 有非常相似的谱线系列。碱金属原子的光谱线主要由4个线系组成:主线系、第一谱线系(漫线系)、 第二辅线系(锐线系)和柏格曼线系(基线系)。进一步对碱金属原子光谱精细结构的研究证实了电了 自旋的存在和原子中电子的自旋与轨道运动的相互作用,这种作用较弱,由它引起了光谱的精细结构。 钠原子光谱及其相应的能级结构具有碱金属原子光谱和能级结构的典型特征。 【实验目的】 1、加强学生对光栅光谱仪的原理和基本组件的了解。 2、对钠原子光谱的进行测量和分析,加深对相关理论的理解与掌握。 3、由钠原子光谱确定各光谱项值及能级值,最子缺△。 【预习思考题】 1、简述光栅光谱仪的主要结构和功能。 2、简述量子缺的形成。 3、简述光色散原理。 【实验器材】 本实验用到的仪器主要有:WGD-8A多功能光栅光谱仪,钠光灯,计算机。 光谱仪是能将入射光按不同波长分成单色光谱的光学仪器,它由准直系统、色散系统和聚焦成像 系统组成。准直系统通常由入射狭缝和准直物镜组成。入射狭缝位于准直物镜的焦平面上。对于光谱 仪来说,入射狭缝实际上是光谱仪的光源,待测信号光经照明系统照射入射狭缝,入射狭缝发出的光 束经准直镜后成为平行光投射到色散系统。 色散元件通常为棱镜,光橱和法布里-珀罗干涉仪。色散元件为光栅的光谱仪称作光橱光谱仪。聚 焦成像系统是利用成象物镜把经过色散系统后,在空间上色散开的各波长的光束会聚或成象在成象物 镜的焦平面上。形成一系列的按波长排列的单色狭缝象,即通常所看到的光谱图。 1负高压调节 6电源开关 2负高压指示 7USB讯号线 3USB口电源指8CCD电缆线 示 9单色仪电缆线 图1-1电箱正视图 9
用多功能光栅光谱仪进行钠光谱测量实验 碱金属原子的光谱和氢原子光谱相似,也可以归纳成一些谱线系列,而且各种不同的碱金属原子具 有非常相似的谱线系列。碱金属原子的光谱线主要由 4 个线系组成:主线系、第一谱线系(漫线系)、 第二辅线系(锐线系)和柏格曼线系(基线系)。进一步对碱金属原子光谱精细结构的研究证实了电子 自旋的存在和原子中电子的自旋与轨道运动的相互作用,这种作用较弱,由它引起了光谱的精细结构。 钠原子光谱及其相应的能级结构具有碱金属原子光谱和能级结构的典型特征。 【实验目的】 1、 加强学生对光栅光谱仪的原理和基本组件的了解。 2、对钠原子光谱的进行测量和分析,加深对相关理论的理解与掌握。 3、由钠原子光谱确定各光谱项值及能级值, 量子缺Δ。 【预习思考题】 1、简述光栅光谱仪的主要结构和功能。 2、简述量子缺的形成。 3、简述光栅色散原理。 【实验器材】 本实验用到的仪器主要有:WGD-8A 多功能光栅光谱仪,钠光灯,计算机。 光谱仪是能将入射光按不同波长分成单色光谱的光学仪器,它由准直系统、色散系统和聚焦成像 系统组成。准直系统通常由入射狭缝和准直物镜组成。入射狭缝位于准直物镜的焦平面上。对于光谱 仪来说,入射狭缝实际上是光谱仪的光源,待测信号光经照明系统照射入射狭缝,入射狭缝发出的光 束经准直镜后成为平行光投射到色散系统。 色散元件通常为棱镜,光栅和法布里-珀罗干涉仪。色散元件为光栅的光谱仪称作光栅光谱仪。聚 焦成像系统是利用成象物镜把经过色散系统后,在空间上色散开的各波长的光束会聚或成象在成象物 镜的焦平面上。形成一系列的按波长排列的单色狭缝象,即通常所看到的光谱图。 1 负高压调节 2 负高压指示 3 USB 口电源指 示 6 电源开关 7 USB 讯号线 8 CCD 电缆线 9 单色仪电缆线 图 1-1 电箱正视图 9