
第四章 刚体B
刚体tB

54-1刚体的运动及其描述 一.刚体模型 刚体:在外力的作用下,大小和形状都不变 的物体 -物体内任意两点的距离不变 二刚体的运动 平动:刚体运动时,其内部任何一条直线 在运动中方向始终不变
§4-1 刚体的运动及其描述 一 .刚体模型 刚体:在外力的作用下,大小和形状都不变 的物体 -物体内任意两点的距离不变 二.刚体的运动 平动:刚体运动时,其内部任何一条直线, 在运动中方向始终不变
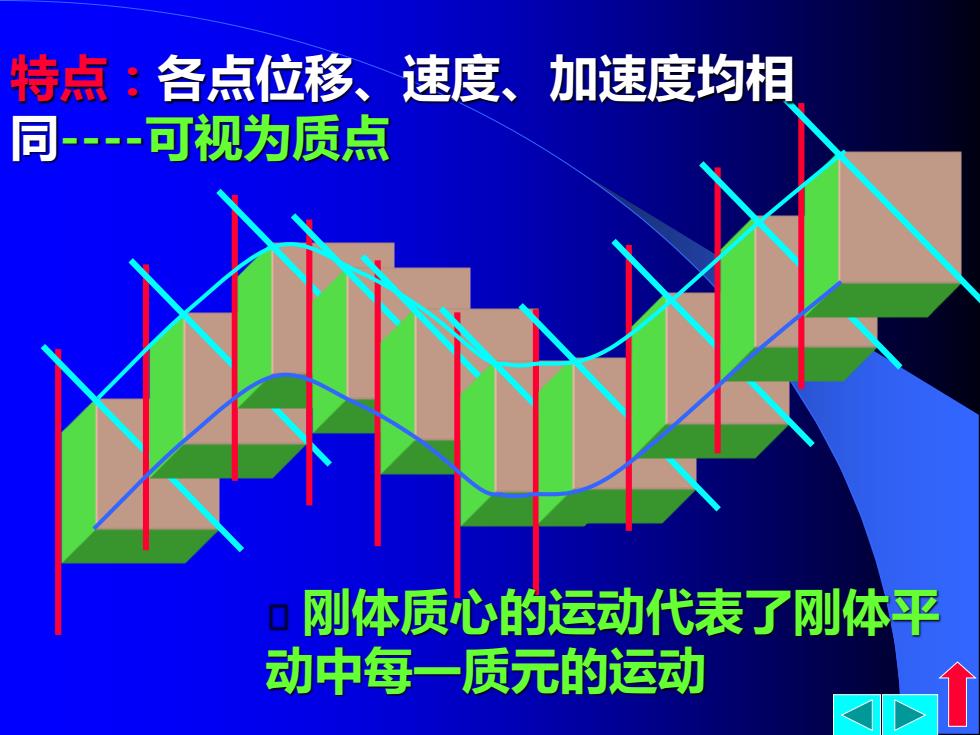
特点:各点位移、速度、加速度均相 同-可视为质点 刚体质心的运动代表了刚体平 动中每一质元的运动
刚体质心的运动代表了刚体平 动中每一质元的运动 特点:各点位移、速度、加速度均相 同-可视为质点
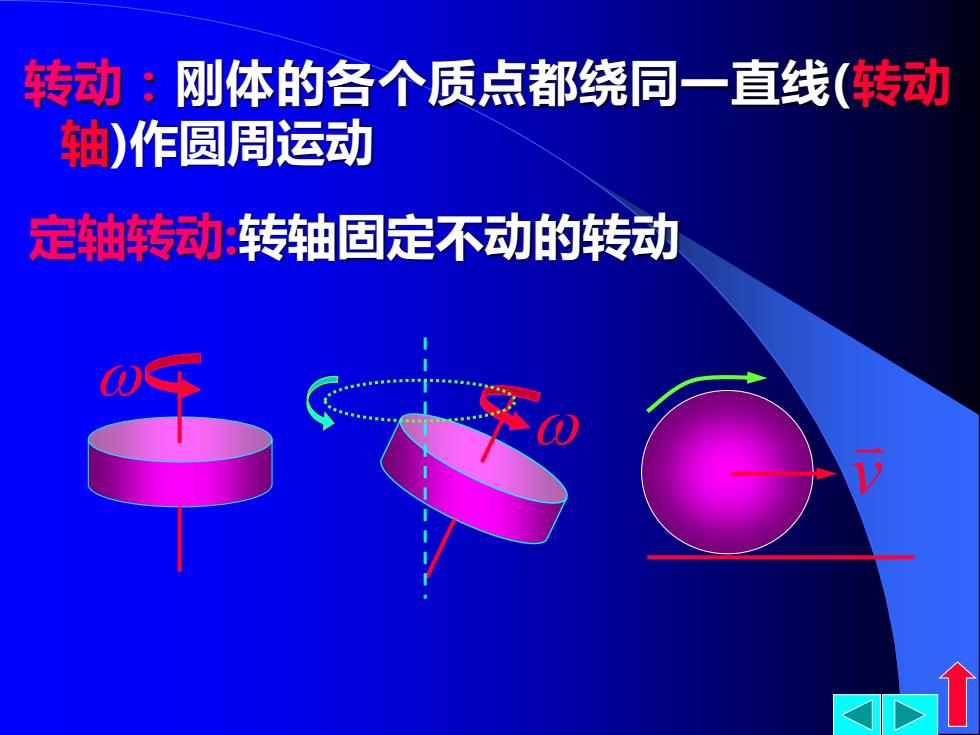
转动:刚体的各个质点都绕同一直线(转动 轴)作圆周运动 定轴转动:转轴固定不动的转动
转动:刚体的各个质点都绕同一直线(转动 轴)作圆周运动 定轴转动:转轴固定不动的转动 v

刚体的一般运动=平动+转动
刚体的一般运动=平动+转动
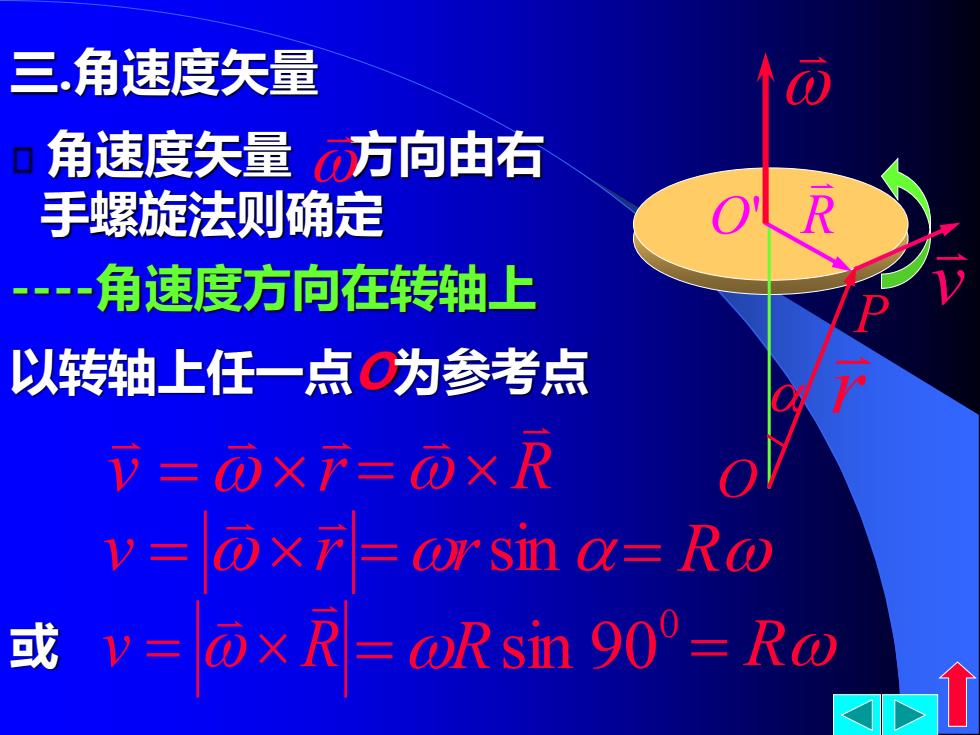
三角速度矢量 角速度矢量方向由右 手螺旋法则确定 角速度方向在转轴上 以转轴上任一点为参考点 立=)×=o×R v= ō×T=or sin a=Ro 或V= D×R=oR sin90°=Ro
三.角速度矢量 -角速度方向在转轴上 角速度矢量 方向由右 手螺旋法则确定 O r R O' v P 以转轴上任一点O为参考点 v r = R = v r = v R 或 = 0 =Rsin 90 = R =rsin= R

d a dt do dr xF+而× dt dδ ×F+而×(而×F) 或 dt a=r,+r⑩en=a,+ann
dt dv a = r ( r) dt d = + 或 dt dr r dt d = + ( r) dt d = t t n n a e a e a r et r en = + 2 = +
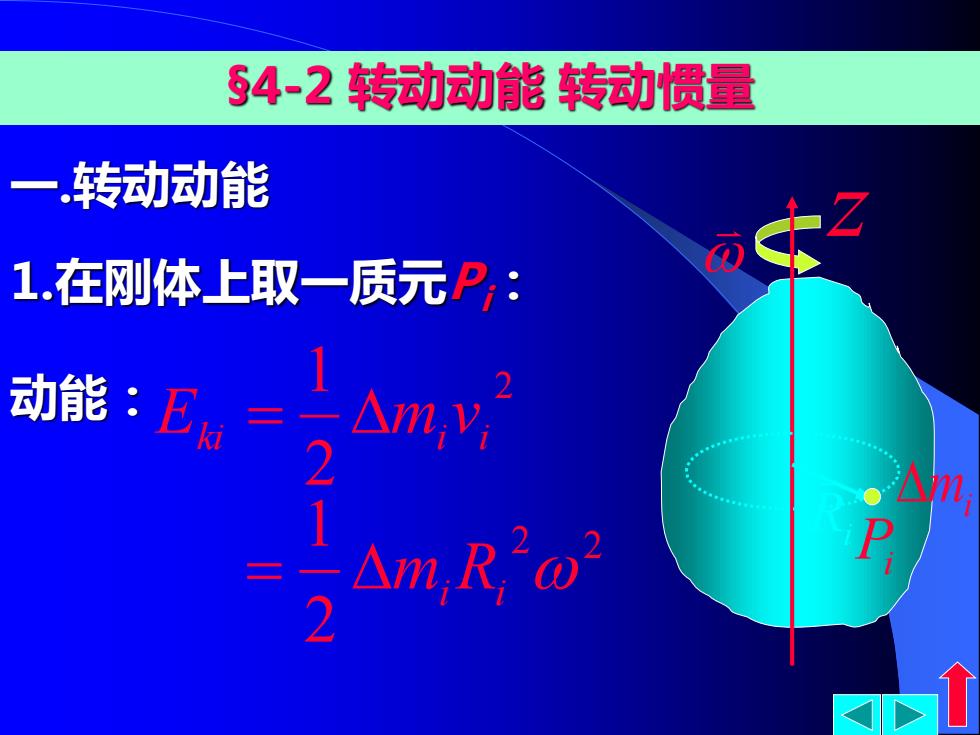
54-2转动动能转动惯量 一转动动能 1.在刚体上取一质元P,: 动能:E=△my, 2 △m,Ro2
z 1.在刚体上取一质元Pi: §4-2 转动动能 转动惯量 一 .转动动能 mi 动能: 2 2 1 ki i i E = m v 2 2 2 1 = mi Ri Ri Pi

2.对刚体上所有质点的动能求和: E=∑Am,Ro2-∑AmR 定义:J.-∑AmRj -对z轴的转动惯量 则刚体的转动动能
2.对刚体上所有质点的动能求和: = 2 2 2 1 Ek mi Ri = i mi Ri 2 2 2 定义: = i z mi Ri J 2 -对z轴的转动惯量 则刚体的转动动能 2 2 1 Ek = J z

二转动惯量 1.对分立的质点系:J=∑△m,R 2.对质量连续分布的刚体:,=「Rdm R-Adl 线分布,入为线密度 R ods 面分布,。为面密度 R ody 体分布,P为体密度 3.转动惯量的物理意义:表示刚体转动时惯 性的大小
二.转动惯量 = i z mi Ri J 2 2.对质量连续分布的刚体: Jz = R dm2 = 1.对分立的质点系: 线分布, 为线密度 面分布, 为面密度 R dV 体分布, 为体密度 2 R ds 2 R dl 2 3.转动惯量的物理意义:Jz表示刚体转动时惯 性的大小