
第章 运动穿具谢 运动守恒
运动守恒下

重点:.1=p2-p - A=FS.cos0 难点:A=F市 ∴.A外+A内=(E6十E6)-(Ea+Epa)
重点: 难点: = 2 1 2 1 p p t t Fdt dp p2 p1 I = − A = FScos = b a A F dr ( ) ( ) A外 + A非内 = Ekb + Ep b − Eka + Ep a

1.力和加速度之间的瞬时效应 -牛顿定律 2.力的时间累积效应 -冲量 3.力的空间累积效应 -功
1.力和加速度之间的瞬时效应 -牛顿定律 2.力的时间累积效应 -冲量 3.力的空间累积效应 -功

3-1牛顿第二定律积分形式之一:动量 定理、动量守恒定律 一质点动量定理 由牛顿定律 dpdt 有Fdt=玩 牛顿定律的微分形式 力在t,一肘闻内的累积量为 Far -dp=D:-Pe
一 .质点动量定理 Fdt dp = -牛顿定律的微分形式 = 2 1 2 1 p p t t Fdt dp §3-1 牛顿第二定律积分形式之一: 动量 定理、动量守恒定律 由牛顿定律 F dp dt = 有 力在 时间内的累积量为 1 2 t →t p2 p1 = −

定义:外力在一段时间内的累积量 称为冲量,即 7=心Fu .1=p2-p 即质点某一时间内所受合外力的冲量等于质 点同一时间内动量的增量 -质点动量定理
= 2 1 t t I Fdt p2 p1 I = − 定义:外力在一段时间内的累积量 称为冲量,即 即质点某一时间内所受合外力的冲量等于质 点同一时间内动量的增量 -质点动量定理
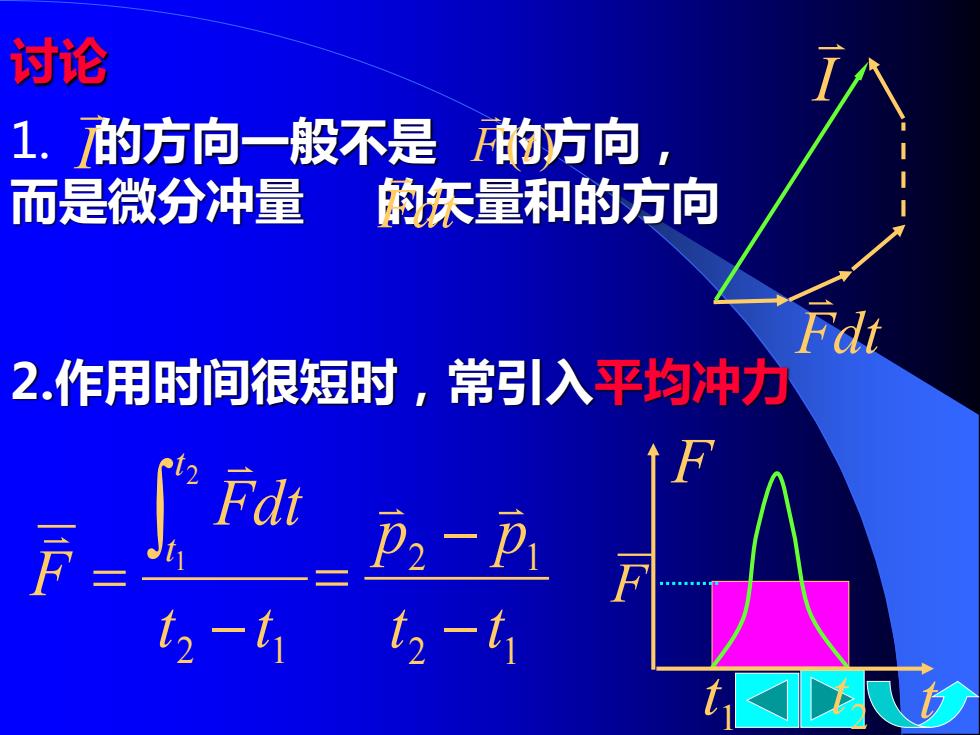
讨论 1.的方向一般不是的方向 而是微分冲量 的东量和的方向 Fdt 2.作用时间很短时,常引入平均冲力 心w-2 t-t -t
F 2.作用时间很短时,常引入平均冲力 2 1 2 1 t t Fdt F t t − = 讨论 1. 的方向一般不是 的方向, 而是微分冲量 的矢量和的方向 F(t) Fdt I Fdt I 1 t 2 t t F 2 1 2 1 t t p p − − =

3.直角坐标系中动量定理的分量形式 I ["F,(t)dt=mvx-mvi ,=F,(d=,-m%, l,=["F.()di=mv=-mv
3.直角坐标系中动量定理的分量形式 = 2 1 ( ) t t x x I F t dt = 2 1 ( ) t t y y I F t dt = mv2x −mv1x = mv2 y − mv1y = 2 1 ( ) t t z z I F t dt= mv2z −mv1z

4.物体的动量相对于不同的惯性系是不同的, 但动量定律不变, 车上成→m Fdt =mv-mv 地上 m(+0)=→m(2+u) Fdt=m(位,+a))-m(氏+)=v-
4.物体的动量相对于不同的惯性系是不同的, 但动量定律不变. u 车上 1 v m 2 v m 1 mv 2 mv 2 1 2 1 Fdt mv mv t t = − 地上 ( ) 1 m v u + ( ) 2 m v u + ( ) ( ) 2 1 2 1 Fdt m v u m v u t t = + − + 2 1 mv mv = −

二质点系动量定理 质点系:由有相互作用的若干个质点组成 的系统 内力:系统内各物体间的相互作用力 外力:系统外物体对系统内物体的作用 力
二.质点系动量定理 质点系:由有相互作用的若干个质点组成 的系统 内 力:系统内各物体间的相互作用力 外 力:系统外物体对系统内物体的作用 力

1.两个质点的质点系 根据牛顿定律 月- F+ha=dr F 冲2 即月内无*五-受 dt f=-f2 dt dt dt
1.两个质点的质点系 m1 m2 21 f 12 f F1 F2 根据牛顿定律 dt dp F f 1 1 1 2 + = dt dp F f 2 2 2 1 + = 相加 dt dp dt dp F F f f 1 2 1 2 1 2 2 1 + + + = + 21 12 f f = − dt dp dt dp F F 1 2 1 2 + = + ( ) 1 2 p p dt d = +