
第四篇电磁学 第九章真空中的静电场 §9-1,2概述 一、电荷与电场 1.电荷:实物的一种属性。 三个基本性质: ①自然界存在两种电荷:正电荷和负电荷 ②电荷守恒 ③电荷的量子化(微观世界的一个基本定律) 最小电量:1.602×10-19库仑 点电荷:不考虑大小和分布状况而可看作集中于一点的电荷。 ①实际有许多情况可以近似成点电荷。 ②点电荷的位置可以方便地在坐标上标出。 电荷守恒定律: 在一个与外界没有电荷交换的系统内,在任一时刻存在于系统中的 正电荷与负电荷的代数和始终保持不变。 ①强调是正负电荷的代数和不变。 ②电荷守恒定律是物理学的基本定律之一。 2.电场 直观上看,电场是给电荷以作用力的物理场。若空间某一区域内各 点具有给予在该点的静止电荷的作用力的属性,就说该区域存在着电场。 电荷一场一电荷 从本质上说:电场是物质的一种存在形式,具有能量、动量和质量。 本章只讨论相对于观察者静止的电荷在其周围空间产生的电场即静电场。 二、库仑定律(实验定律:1785年;电磁学从定性到定量的重要里程碑) 表示两个相对静止的点电荷之间的相互作用的定律,是静电学的基础
第四篇 电磁学 第九章 真空中的静电场 §9-1,2 概述 一、电荷与电场 1.电荷:实物的一种属性。 三个基本性质: ① 自然界存在两种电荷:正电荷和负电荷 ② 电荷守恒 ③ 电荷的量子化(微观世界的一个基本定律) 最小电量: 19 1.602 10− 库仑 点电荷:不考虑大小和分布状况而可看作集中于一点的电荷。 ① 实际有许多情况可以近似成点电荷。 ② 点电荷的位置可以方便地在坐标上标出。 电荷守恒定律: 在一个与外界没有电荷交换的系统内,在任一时刻存在于系统中的 正电荷与负电荷的代数和始终保持不变。 ① 强调是正负电荷的代数和不变。 ② 电荷守恒定律是物理学的基本定律之一。 2. 电场 直观上看,电场是给电荷以作用力的物理场。若空间某一区域内各 点具有给予在该点的静止电荷的作用力的属性,就说该区域存在着电场。 电荷 场 电荷 从本质上说:电场是物质的一种存在形式,具有能量、动量和质量。 本章只讨论相对于观察者静止的电荷在其周围空间产生的电场即静电场。 二、库仑定律(实验定律;1785 年;电磁学从定性到定量的重要里程碑) 表示两个相对静止的点电荷之间的相互作用的定律,是静电学的基础

=l=k84✉;方=-元=k94正=k94元 r ri2ri2 2 7429万 →⊕→ ←⊙ 注意: ①国际单位制[S]中,k=8.988×10N·m2.c2, 而电磁学部分MKSA有理制中 ,;6-8.85×10-12C2.N-m2 1494。 方无装轻病号 ②满足“平方反比律”,这种力称为“库仑力”或“静电力” ③两静止电荷之间的静电力虽然满足大小相等,方向相反,作用在一条 直线上,但不是一对作用力与反作用力。 例题9-1:在氢原子内,电子和原子核之间的距离为r=0.529×10-0m。试计算电子和 原子核之间的静电作用力和万有引力并比较两者大小。又设原子核中的两质子相距 5=4.0×10-5m,求此两质子之间的静电力。 解:已知m。=9.11x10-kg,M氯楼=1.67×10kg 9,=42=1.6×10-9C,G。=6.67x10-1"Nm2.kg2 94=900x10°×06x10-2 人.=46了 (0.529x100y-823x10-*N f=GAm=66x101T×6Zx10-27 -=3.64×10-47N (0.529×10-10)y2 会-2i045=5g-90860号=1w
2 12 1 2 12 21 r q q f = f = k ; 3 12 12 1 2 12 12 2 12 1 2 21 12 r r q q k r r r q q f f k = − = = 12 f 1 q 12 r 2 q 21 f 注意: ① 国际单位制[SI]中, 9 2 2 8.988 10 − k = N m c , 而电磁学部分 MKSA 有理制中 4 0 1 k = ; 12 2 1 2 0 8.85 10− − − = C N m 3 12 12 1 2 12 0 12 2 12 1 2 0 21 12 4 1 4 1 r r q q r r r q q f f = − = = ② 满足“平方反比律”,这种力称为“库仑力”或“静电力” ③ 两静止电荷之间的静电力虽然满足大小相等,方向相反,作用在一条 直线上,但不是一对作用力与反作用力。 例题 9-1:在氢原子内,电子和原子核之间的距离为 r m 10 1 0.529 10− = 。试计算电子和 原子核之间的静电作用力和万有引力并比较两者大小。又设原子核中的两质子相距 r m 15 2 4.0 10− = ,求此两质子之间的静电力。 解:已知 me kg 31 9.11 10− = , M 氢核 = kg 27 1.67 10− q q C 19 1 2 1.6 10− = = , 11 2 2 0 6.67 10− − G = N m k g N r q q f e 8 1 0 2 1 9 2 9 2 1 1 2 0 8.23 10 (0.529 10 ) (1.6 10 ) 9.00 10 4 1 − − − = = = N r Mm f m G 4 7 1 0 2 3 1 2 7 1 1 2 1 0 3.64 10 (0.529 10 ) 9.11 10 1.67 10 6.67 10 − − − − − = = = 39 = 2.2710 m e f f ; N r q q Fe 14 (4.0 10 ) (1.6 10 ) 9 10 4 1 15 2 19 2 9 2 1 1 0 = = = − −

§9-3电场强度 1.电场强度矢量E:E=E ;E单位:牛/仑或伏/米 90 它是定量描写电场中各点性质的物理量,是描写电场性质最基本的物理量。 试探电荷q。应满足: ①体积很小以便确定场中每点的性质。 ②电量很小,不影响原来电场的分布。 2。场强迭加原理(迭加原理是经典电磁学的一条基本原理) 当9置于91:92,9,9.产生的场时,分别受到g,92,9,9 的力为万,万,f;由实验知:了=万+方+.了n 969096 3.场强的计算: (1)点电荷电场中的场强: 源点 90 p场点 0) 原点 真空中: 199 了=46F7
§9-3 电场强度 1.电场强度矢量 E : q0 F E = ; E 单位:牛/仑或伏/米 它是定量描写电场中各点性质的物理量,是描写电场性质最基本的物理量。 试探电荷 0 q 应满足: ① 体积很小以便确定场中每点的性质。 ② 电量很小,不影响原来电场的分布。 2.场强迭加原理(迭加原理是经典电磁学的一条基本原理) 当 0 q 置于 q q q qn , , , , 1 2 3 产生的场时,分别受到 q q q qn , , , , 1 2 3 的力为 n f f f , , , 1 2 ;由实验知: n f f f f = + + 1 2 得: n n E E E q f q f q f q f E = = + ++ = 1 + 2 ++ 0 0 2 0 1 0 3.场强的计算: (1)点电荷电场中的场强: 真空中: r r r qq f 2 0 4 0 1 = ; r r r q E 2 4 0 =

(2)点电荷系电场中的场强 原点 Ux 设真空中有9,92,9.,9n个电荷 4π62 由迭加原理: E=E+E,++瓦-2,9 4π6r (3)任意带电体电场中的场强 影 E-e- 对于线电荷分布,线密度为入 对于面电荷分布,面密度为σ E= 对于体电荷分布,体密度为 E=顶:
(2)点电荷系电场中的场强 设真空中有 q q q qn , , , , 1 2 3 个电荷 1 1 2 0 1 1 1 4 r r r q E = , = 2 2 2 0 2 2 2 4 r r r q E n n n n n r r r q E 2 4 0 = 由迭加原理: = = + ++ = n i i i i i n r r r q E E E E 1 2 0 1 2 4 (3)任意带电体电场中的场强 r r r dq dE 2 4 0 1 = = = r r dq E dE 3 4 0 对于线电荷分布,线密度为 = L r r dl E 3 4 0 1 对于面电荷分布,面密度为 r r dS E S = 3 4 0 1 对于体电荷分布,体密度为 = V r r dV E 3 4 0 1
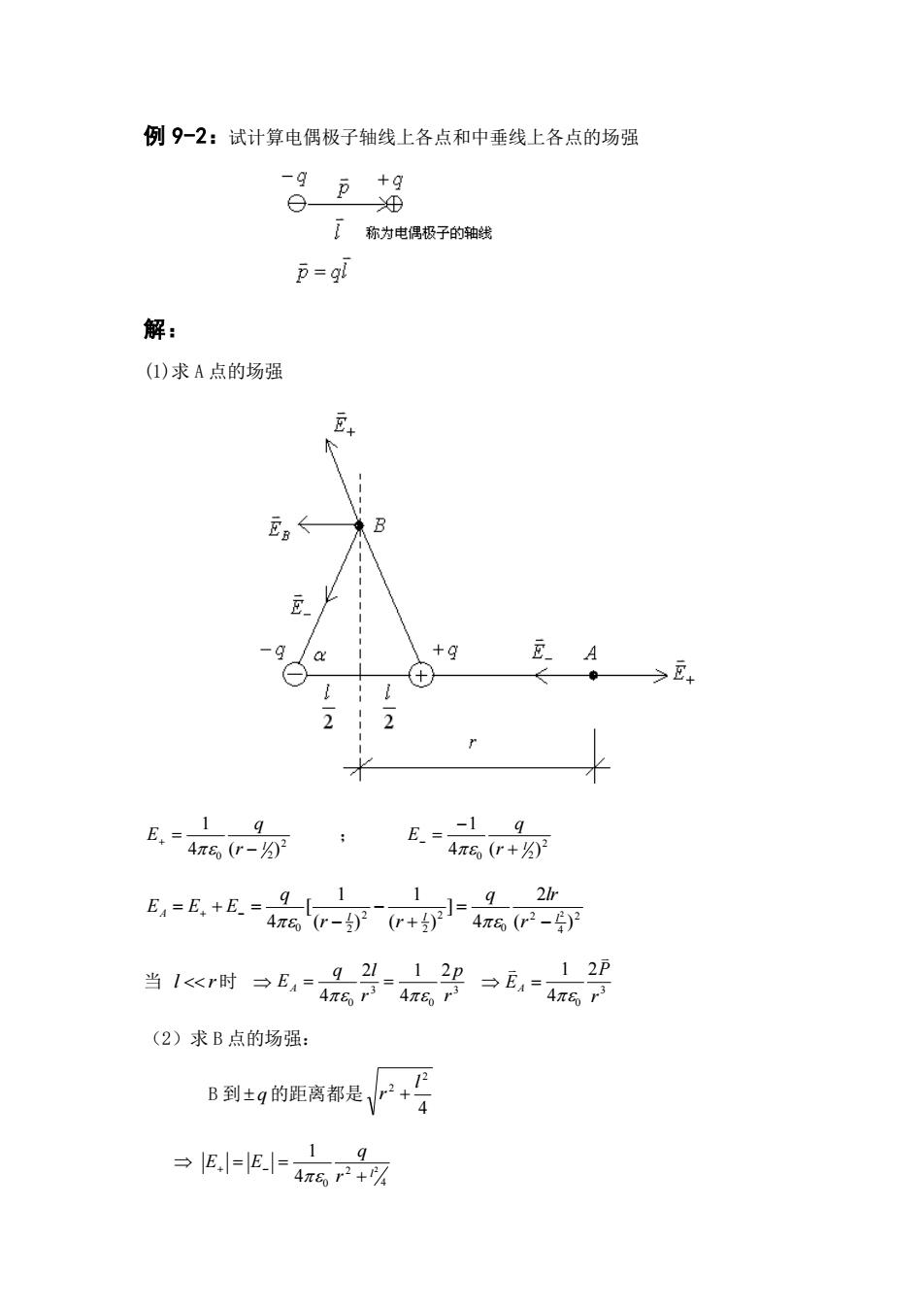
例9-2:试计算电偶极子轴线上各点和中垂线上各点的场强 日月超 了称为电偶极子的轴线 p=gl 解: (I)求A点的场强 2 E.=4+ -1 E,=46-万 (2)求B点的场强: B到的距离都是 →E.=E.4r产+7 9
例 9-2:试计算电偶极子轴线上各点和中垂线上各点的场强 解: (1)求 A 点的场强 2 0 2 4 ( ) 1 l r q E − + = ; 2 0 2 4 ( ) 1 l r q E + − − = 2 4 2 0 2 2 2 0 2 ( ) 2 4 ] ( ) 1 ( ) 1 [ 4 2 l l l A r q lr r r q E E E − = + − − = + + − = 当 l r 时 3 0 3 0 2 4 2 1 4 r p r q l EA = = 3 0 2 4 1 r P EA = (2)求 B 点的场强: B 到 q 的距离都是 4 2 2 l r + 4 2 0 2 4 1 l r q E E + + = − =

仅考虑大小:EB=2E,cosa=2E.cosa 又cosa=F+7 曰B46+4 1 al 当1r时心2+=r 例9-3:试计算均匀带电圆环轴线上任一给定点P处的场强,设圆环 的半径为R,周长为L,所带的电量为q,p点与环心的距离为x 解:在圆环上任取一个微元d山,d山的带电量d内=品山 d dE〦 de 微元电有在P点产生的肠强为正,其大小E=亭欲 它可作分解如图所示,由对称性得: fdE〦:o →E=fdEw=dE cos0 因,0都相同:→B=52可 19c0s
仅考虑大小: EB = 2E+ cos = 2E− cos 又 4 2 2 2 cos l l r + = 2 3 ) 4 ( 4 1 2 2 0 l r ql EB + = 当 l r 时 3 2 2 2 3 ) 4 ( r l r + = 3 0 3 4 0 4 1 r p r ql EB = = 3 4 0 1 r P EB = − 例 9-3:试计算均匀带电圆环轴线上任一给定点 P 处的场强,设圆环 的半径为 R,周长为 L,所带的电量为 q,p 点与环心的距离为 x 解:在圆环上任取一个微元 dl ,dl 的带电量 dl R q dq 2 = 微元电荷在 P 点产生的场强为 dE ,其大小 2 0 2 0 1 4 2 1 4 1 R r qdl r dq dE = = 它可作分解如图所示,由对称性得; // cos = = L L E dE dE 因 r , 都相同; 2 0 cos 4 1 r q E =

由图:c0s0= :r2=R2+x2 1 讨论: 当》R时,日=G是相首于点电新, 当x=0时,E=0即为圆心处的场强 §9-4高斯定理(可由库仑定律和场强迭加原理导出) 在真空中的任何静电场中,通过任一闭合曲面的电场强度通量等于该 闭合曲面所包围的电荷的代数和的6,分之一,与闭合曲面以外的电荷无关。 fE西=号24 关于高斯定理的几点说明: 1.它是静电场及电磁学的基本定律,表明静电场是有源场,电场是电力线的源。 2.高斯定理中,E是总场。高斯定理中表示穿过闭合曲面的电通量,仅由闭曲 面内电荷所决定。 3.高斯定理对静电场是普遍适用的,但仅对电荷分布具有空间对称性的电荷系 统才有可能用此定理计算场强。 高斯定理推导分四步: 1.点电荷位于单位球面的球心。 2.点电荷位于任意闭合曲面内 3.点电荷位于任意闭合曲面外 4.由迭加原理,闭合曲面包围带电量为q的带电体 [提一下介质中的高斯定理]
由图: r x cos = ; 2 2 2 r = R + x 2 3 4 ( ) 1 2 2 0 x R qx E + = 讨论: 当 x R 时, 2 4 0 1 x q E = 相当于点电荷。 当 x = 0 时, E = 0 即为圆心处的场强。 §9-4 高斯定理(可由库仑定律和场强迭加原理导出) 在真空中的任何静电场中,通过任一闭合曲面的电场强度通量等于该 闭合曲面所包围的电荷的代数和的 0 分之一,与闭合曲面以外的电荷无关。 即: = i S E dS q 0 1 关于高斯定理的几点说明: 1.它是静电场及电磁学的基本定律,表明静电场是有源场,电场是电力线的源。 2.高斯定理中, E 是总场。高斯定理中表示穿过闭合曲面的电通量,仅由闭曲 面内电荷所决定。 3.高斯定理对静电场是普遍适用的,但仅对电荷分布具有空间对称性的电荷系 统才有可能用此定理计算场强。 高斯定理推导分四步: 1.点电荷位于单位球面的球心。 2.点电荷位于任意闭合曲面内 3.点电荷位于任意闭合曲面外 4.由迭加原理,闭合曲面包围带电量为 q 的带电体。 [提一下介质中的高斯定理]

高斯定理的证明: 上点电背位于单位球的中心:月否-月容号 2.点电荷位于闭合曲面内: 的6-药品品如号 3.点电荷位于闭合曲面之外: E-E+E=-袋+ =-品n+m=0 4.对多个点电荷,分别处于闭合曲面之内或之外,利用迭加原理立即可得。 高斯定理的应用: 对具有对称性的情形,能够直接运用高斯定理,求场强往往比较简单。 例题9-4:求均匀带电球体的电场,该球的介电常数为6。,半径为R, 电荷体密度为p,总电荷为g 解:g=Rp;月E西=g
高斯定理的证明: 1.点电荷 q 位于单位球的中心: = = S S q r qdS E dS 0 2 4 0 2.点电荷位于闭合曲面内: = = = = S S S q d q r q dS r qdS E dS 0 0 2 0 2 0 4 4 4 3.点电荷位于闭合曲面之外: = + = − + S S S S S r qdS r qdS E dS E dS E dS 1 2 1 2 2 0 2 2 0 1 4 4 0 4 0 4 0 ' = − + = d q d q 4.对多个点电荷,分别处于闭合曲面之内或之外,利用迭加原理立即可得。 高斯定理的应用: 对具有对称性的情形,能够直接运用高斯定理,求场强往往比较简单。 例题 9-4:求均匀带电球体的电场,该球的介电常数为 0 ,半径为 R, 电荷体密度为 ,总电荷为 q 解: 3 3 4 q = R ; = 1 0 1 ' S q E dS

当R时:月医,西=号=64 例题95:在半径为R和R,的两个同心球面上,分别均匀地分布着电荷Q,和Q, 求:(1)1,Ⅱ,Ⅲ三个区域内的场强分布: (2)若Q,=-Q,时情况如何?画出此情况的E一r曲线。 解:由分析知,问题具有球对称性,取球形高斯面。 (1)当rR时,月E,5=+ 6-89 (2)当Q=-Q,时→E,=0:E,和E2同上
当 r1 R 时: 3 3 1 3 4 0 3 1 0 2 1 1 3 1 4 3 1 4 4 r R q E r r = = 得: 3 1 0 1 4 r R q E = 当 r2 R 时: = = 2 2 2 0 2 0 2 4 S E r q E dS 得: 2 0 2 2 4 r q E = 例题 9-5:在半径为 R1 和 R2 的两个同心球面上,分别均匀地分布着电荷 Q1 和 Q2 , 求: (1)Ⅰ,Ⅱ,Ⅲ三个区域内的场强分布; (2)若 Q1 = −Q2 时情况如何?画出此情况的E-r 曲线。 解: 由分析知,问题具有球对称性,取球形高斯面。 (1)当 R1 r 时, 0 1 0 1 1 = = E dS q S E1 = 0 当 1 R2 R r 时, = 2 0 1 2 S Q E dS r r Q E 3 0 1 2 4 = 当 R2 r 时, + = 3 0 1 2 3 S Q Q E dS r r Q Q E 3 0 1 2 3 4 + = (2)当 Q1 = −Q2 时 E3 = 0 ; E1 和 E2 同上

小E 0 §9-5电场力的功电势 1.与重力场对照: 在点电荷电场中g。从a→b, dA=F.dl =goE.dl =go Edlcos0=go Edr 9 9o为al 电场力的功: -8i-2之 对一般静电场,可以看成电荷的选加 -5i-2照之 引入电势能
§9-5 电场力的功 电势 1.与重力场对照: 在点电荷电场中 0 q 从 a →b, dA F dl q E dl q Edl q Edr 0 0 0 = = = cos = 电场力的功: = = = − b a a b b a ab r r q q A dA q E dl ) 1 1 ( 4 0 0 0 对一般静电场,可以看成电荷的迭加 = = − = b a ia ib i n i ab r r q q A q E dl ) 1 1 ( 4 0 0 1 0 引入电势能