
第五篇量子物理 第二十章早期量子论和量子力学基础 820.1辐热射普朗克的量子假说 一、热辐射 任何物体(固体或液体)在任何温度下都向外发射各种波长的电磁波。在一定时间内,物体向 外发射电磁波的总能量(辐射能)以及该能量按波长的分布都与物体的温度密切相关。这种现象称 为热辐射。 (热传递:1.热传导2.热对流3.热辐射) 二、基尔霍夫辐射定律 1.辐出度M(T) 单位时间从物体表面单位面积上所发射的各种波长的总辐射能,用M(T表示,是温 度的函数,单位:W/m 2.单色辐出度M.() 单位时间从物体表面单位面积上所发射的波长在A-入+d入内的辐出能dM,与波长 间隔dA之比:M(T)=dM/AAM(T)与A、T有关,单位:W/m品. 在某特定温度T下,有M(T)=∫M,(T)dn 3.吸收比和反射比 物体吸收能量与入射能量比称为吸收比α(入、T),物体反射能量与入射能量比称 为反射比r(入、T)。当入射能量的波长在X-入+d入内时,则a(X、T),r(x、T)分 别称为单色吸收比和单色反射比。 对不透明的物体:a(入、T)+r(入、T)=1 4.基尔霍夫定律 在热平衡下(同一温度),各种不同物体对相同波长的单色辐出度与单色吸收比之
第五篇 量子物理 第二十章 早期量子论和量子力学基础 §20.1 辐热射 普朗克的量子假说 一、热辐射 任何物体(固体或液体)在任何温度下都向外发射各种波长的电磁波。在一定时间内,物体向 外发射电磁波的总能量(辐射能)以及该能量按波长的分布都与物体的温度密切相关。这种现象称 为热辐射。 (热传递:1.热传导 2.热对流 3.热辐射) 二、基尔霍夫辐射定律 1.辐出度 M(T) 单位时间从物体表面单位面积上所发射的各种波长的总辐射能,用 M(T)表示,是温 度的函数,单位:W/m 2 . 2.单色辐出度 Mλ(T) 单位时间从物体表面单位面积上所发射的波长在λ-λ+dλ内的辐出能 dMλ与波长 间隔 dλ之比: Mλ(T)= dMλ/dλ Mλ(T)与λ、T 有关,单位:W/m 3 . 在某特定温度 T 下,有 = 0 M (T) M (T)d 3.吸收比和反射比 物体吸收能量与入射能量比称为吸收比α(λ、T),物体反射能量与入射能量比称 为反射比 r(λ、T)。当入射能量的波长在λ-λ+dλ内时,则α(λ、T),r(λ、T)分 别称为单色吸收比和单色反射比。 对不透明的物体:α(λ、T)+r(λ、T)=1 4.基尔霍夫定律 在热平衡下(同一温度),各种不同物体对相同波长的单色辐出度与单色吸收比之
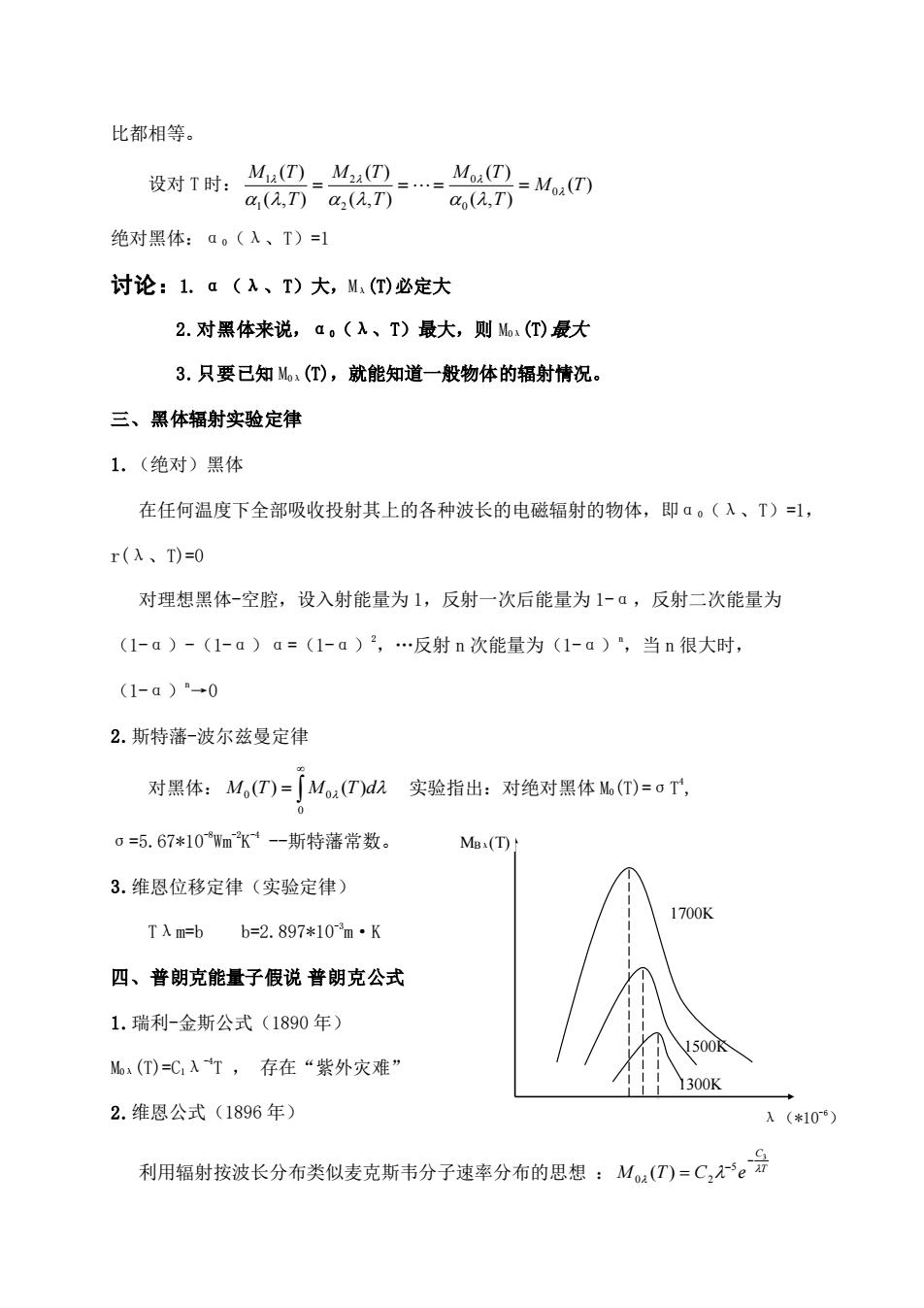
比都相等。 设对T时:-4==,=M( 4(2T)a(元,T) a(i,T) 绝对黑体:a。(入、T)=1 讨论:1.a(入、T)大,M,(T)必定大 2.对黑体来说,ā。(x、T)最大,则M(T)最大 3.只要已知M(T),就能知道一般物体的辐射情况。 三、黑体辐射实验定律 1.(绝对)黑体 在任何温度下全部吸收投射其上的各种波长的电磁辐射的物体,即α。(入、T)=l, r(入、T)=0 对理想黑体-空腔,设入射能量为1,反射一次后能量为1-α,反射二次能量为 (1-a)-(1-a)a=(1-a)2,.反射n次能量为(1-a)",当n很大时, (1-a)"→0 2.斯特藩-波尔兹曼定律 对黑体:M,(T)=「Mo(T)d实验指出:对绝对黑体M(T)=oT, 0=5.67*10mK-一斯特藩常数。 Ma(T) 3.维恩位移定律(实验定律) 700K Tλm=bb=2.897*10m·K 四、普朗克能量子假说普朗克公式 1.瑞利-金斯公式(1890年) M(T)=C入T,存在“紫外灾难” 1300K 2.维恩公式(1896年) 入(*10 利用辐射按波长分布类似麦克斯韦分子速率分布的思想:M(们=C,。号
比都相等。 设对 T 时: ( ) ( , ) ( ) ( , ) ( ) ( , ) ( ) 0 0 0 2 2 1 1 M T T M T T M T T M T = == = 绝对黑体:α0(λ、T)=1 讨论:1. α(λ、T)大,Mλ(T)必定大 2.对黑体来说,α0(λ、T)最大,则 M0λ(T)最大 3.只要已知 M0λ(T),就能知道一般物体的辐射情况。 三、黑体辐射实验定律 1.(绝对)黑体 在任何温度下全部吸收投射其上的各种波长的电磁辐射的物体,即α0(λ、T)=1, r(λ、T)=0 对理想黑体-空腔,设入射能量为 1,反射一次后能量为 1-α,反射二次能量为 (1-α)-(1-α)α=(1-α)2,.反射 n 次能量为(1-α)n,当 n 很大时, (1-α)n→0 2.斯特藩-波尔兹曼定律 对黑体: = 0 0 0 M (T) M (T)d 实验指出:对绝对黑体 M0(T)=σT 4 , σ=5.67*10-8 Wm-2 K -4 -斯特藩常数。 3.维恩位移定律(实验定律) Tλm=b b=2.897*10-3 m·K 四、普朗克能量子假说 普朗克公式 1.瑞利-金斯公式(1890 年) M0λ(T)=C1λ-4 T , 存在“紫外灾难” 2.维恩公式(1896 年) 利用辐射按波长分布类似麦克斯韦分子速率分布的思想 : T C M T C e 3 5 0 2 ( ) − − = λ(*10-6) MBλ(T) 1300K 1500K 1700K

以上两公式虽然与实验不符,但暴露了经典物理学的缺陷。 3.能量子假说普朗克公式 振子能量只能取一些分立值(各分状态):e,2e,3e,.,ne,n为正整数,称 为量子数。 对频率为v的谐振子来说,最小能量为e=hv,其中h=6.63*10J·S 按照以上假说和麦克斯韦-玻尔兹曼分布律得:普朗克公式: M,(①=2hCx=2hCx,1,其中C为光速,K为玻尔兹曼常数。 e标-1 e行-1 §20.2光电效应爱因斯坦的光子理论 一、光电效应的实验规律 当光照射在金属表面时,金属中有电子逸出的现象叫做光电效应。所逸出得劲电子 叫光电子,所形成的电流称为光电流。 1.入射光的频率不变时的伏安特性曲线 2.入射光的强度不变时的伏安特性曲线 Is 光强较强 光强较弱 0 0 光强不变 Ua频率不变 从以上曲线看出: (1)当U足够大时,阴极K上逸出的电子全部被阳极A吸收。Is称为饱和电流,Is与 入射光强成正比
以上两公式虽然与实验不符,但暴露了经典物理学的缺陷。 3.能量子假说 普朗克公式 振子能量只能取一些分立值(各分状态):ε,2ε,3ε,.,nε,n 为正整数,称 为量子数。 对频率为ν的谐振子来说,最小能量为ε=hν,其中 h=6.63*10-34J·S 按照以上假说和麦克斯韦-玻尔兹曼分布律得:普朗克公式: 1 1 2 1 1 ( ) 2 2 5 2 5 0 − = − = − − KT h K T hC e hC e M T hC ,其中 C 为光速,K 为玻尔兹曼常数。 §20.2 光电效应 爱因斯坦的光子理论 一、光电效应的实验规律 当光照射在金属表面时,金属中有电子逸出的现象叫做光电效应。所逸出得劲电子 叫光电子,所形成的电流称为光电流。 1.入射光的频率不变时的伏安特性曲线 2.入射光的强度不变时的伏安特性曲线 从以上曲线看出: (1)当 U 足够大时,阴极 K 上逸出的电子全部被阳极 A 吸收。Is 称为饱和电流,Is 与 入射光强成正比 I 光强较强 光强较弱 0 Ua U 频率不变 0 U Is 光强不变

(2)存在遏止电压,对应与电子逸出的最大初动能。 2m=c0. 且U。=Kv-U。,K,o>0,%与金属有关的恒量,K是普适恒量。 (3)分析与实验得: 2≥03v≥受6-是称为光电效应的红限频率。 (4)光照到金属上立即有光电子逸出,经历的时间△。时,即使光强度很微弱,在△<10”秒内即可有光电子产生。 二、光的波动说的缺陷 按波动说:光能量∝振幅的平方,即辐射能决定于光的强度,在解释光电效应时主 要有三点困难: (1)按波动说,光电子初动能∝入射光强: (2)不应存在红限y。,只要光强足够大,就可有光电子: (3)按波动说,辐射能连续分布在被照射的空间并以光速传播,所以从光照射到有光 电子出现,需要一段积累时间,且入射光越弱,时间越长
(2)存在遏止电压,对应与电子逸出的最大初动能。 m Ua mv = e 2 2 1 且 Ua = K −U0 ,K,U0>0 , U0与金属有关的恒量,K 是普适恒量。 (3)分析与实验得: 0 2 1 0 0 2 0 K U K U mvm = 称为光电效应的红限频率。 (4)光照到金属上立即有光电子逸出,经历的时间 t 10−9秒。 总结四条: (1)饱和电流 Is 的大小与入射光的强度成正比,即单位时间内光电子数与入射光的强 度成正比; (2)遏止电压 Ua 与入射光强度无关,只与入射光的频率ν有关,ν大, Ua 大,电子初动能 大; (3)对于一定的金属,存在一红限 0 ,当光的 0 时,不论光强如何,照射时间多长,均无光 电子,不同的金属 0 也不同; (4)当 0 时,即使光强度很微弱,在 t 10−9秒 内即可有光电子产生。 二、光的波动说的缺陷 按波动说:光能量 振幅的平方,即辐射能决定于光的强度,在解释光电效应时主 要有三点困难: (1)按波动说,光电子初动能 入射光强; (2)不应存在红限 0 ,只要光强足够大,就可有光电子; (3)按波动说,辐射能连续分布在被照射的空间并以光速传播,所以从光照射到有光 电子出现,需要一段积累时间,且入射光越弱,时间越长

三、爱因斯坦光子理论(1905年) 1.光是一种在真空中以速度C传播的粒子流,这种粒子称为光量子(光子),每个光子 能量为: E=h v. 若单位时间通过单位面积的光子数为N 则能流密度大小为:S=hv 2.按光子的概念 光子与金属中束缚电子相互作用而被吸收,产生电子,按能量守恒和转换定律: hv=m+A 称为爱因斯坦光电效应方程。 解释光电效应: (1)光电子数c光子数,饱和电流1sx光电子数 一Isx光子数,即Isx入射光强 (2)大,5mm2大U大 (3)要使有光电子产生,必m220.即hv之4v2,=合,红限存在. (4)电子能一次全部吸收光子能量,不必积累时间。 四、光子的质量和动量 s=hv p=m,C=g-身 光在传播时表现出波动性,在与物质相互作用时表现出粒子性的一面
三、爱因斯坦光子理论(1905 年) 1.光是一种在真空中以速度 C 传播的粒子流,这种粒子称为光量子(光子),每个光子 能量为: ε=hν, 若单位时间通过单位面积的光子数为 N 则能流密度大小为:S=Nhν 2.按光子的概念 光子与金属中束缚电子相互作用而被吸收,产生电子,按能量守恒和转换定律: h = mv + A 2 2 1 称为爱因斯坦光电效应方程。 解释光电效应: (1)光电子数 光子数,饱和电流 Is 光电子数 Is 光子数,即 Is 入射光强 (2) 大, mv 2大,Ua 大 2 1 (3)要使有光电子产生,必 h A mv h A 0 = 2 0, , 2 1 即 ,红限存在。 (4)电子能一次全部吸收光子能量,不必积累时间。 四、光子的质量和动量 = = = = = = h C h p C C h C m m h 2 2 光在传播时表现出波动性,在与物质相互作用时表现出粒子性的一面

§20.3康普顿效应 一、康普顿实验 1923年康普顿研究X射线(6*10Hz-7.5*10Hz)经金属、石墨等物质散射后的光谱 成分,近一步证实了光的粒子性。 实验结果:散射线中除了与入射线波长入。相同射线外,也有入>入。的射线,称为康 普顿效应,但: 1.原子量小的物质,康普顿散射强,原子量大的物质,康普顿散射弱。 2.康普顿位移△1=1-1,仅与散射角有关,而与物质无关。 二、经典波动观点的困难 v的X射线对电子作用。 电子的v振动,辐射v的电磁波,无法解释。 三、康普顿用光子理论解释 认为康普顿效应是光子与静止自由电子发生弹性碰撞的结果。 1.按能量-动量守恒,光子只失去部分能量,产生康普顿位移: 2.光子与原子实碰撞,能量近似不变,存在的X射线: 3.原子量小,康普顿散射强:原子量大,康普顿散射弱。 强守之气仁所 ① 能量守恒:hy。+m,C2=hv+mC ③ 从式中看出:(m=(岂>+(2》-2c0s0 ③ cC 解②,③式得 d=-=0-c00)=之cm9 h
§20.3 康普顿效应 一、康普顿实验 1923 年康普顿研究X射线(6*1016Hz-7.5*1019Hz)经金属、石墨等物质散射后的光谱 成分,近一步证实了光的粒子性。 实验结果:散射线中除了与入射线波长λ0相同射线外,也有λ>λ0的射线,称为康 普顿效应,但: 1.原子量小的物质,康普顿散射强,原子量大的物质,康普顿散射弱。 2.康普顿位移 = − 0 仅与散射角有关,而与物质无关。 二、经典波动观点的困难 的X射线对电子作用, 电子的 振动,辐射 的电磁波,无法解释。 三、康普顿用光子理论解释 认为康普顿效应是光子与静止自由电子发生弹性碰撞的结果。 1.按能量-动量守恒,光子只失去部分能量,产生康普顿位移; 2.光子与原子实碰撞,能量近似不变,存在 0 的X射线; 3.原子量小,康普顿散射强;原子量大,康普顿散射弱。 动量守恒: n mv C h n C h = + 0 0 ① 能量守恒: 2 2 h 0 + m0C = h + mC ② 从式中看出: = + − COS C h C h C h C h mv 2 2 0 2 0 ( ) ( ) ( ) 2 ③ 解②,③式得: ) 2 (1 ) ( 2 0 0 0 D Sin m C h COS m C h = − = − =

§20.4氢原子光谱玻尔的氢原子理论 原子量子理论概述: 1897年发现电子并确认电子是原子的组成粒子 1900年普朗克第一次提出量子假说 1905年爱因斯坦提出光量子假说 不久汤姆逊最早提出一个原子结构模型 1911年卢瑟福提出原子有核模型 1913年玻尔根据卢瑟福的原子有核模型以及原子光谱的规律性,提出氢原子的量子 理论,初步奠定了原子物理学的基础 1924年德布罗意提出实物粒子(如电子)与光子一样,也具有波-粒二象性假说 之后在此基础上,薛定谔、海森伯等人建立了新的量子力学。量子力学的建立标志 着人类对物质结构的认识有了新的突破。 从192?年开始量子力学用于固体物理领域,从而促进了对固体材料、半导体、激光、 超导等的研究。 一、氢原子光谱的规律性 1.光谱 研究原子结构的重要途径之一,是电磁辐射的波长成分和强度分布的记录。光谱可分 为三类:1.线状光谱2.带状光谱3.连续光谱另还可分为发射和吸收光谱。 2.氢原子光谱 1885年从某些星体的光谱中已观测氢谱线已达14条,瑞士科学家巴耳末发现有简单 n 规律: 1=Bn-4n=345 称为巴耳末公式。 其中B=3645.6A 所对应的一组谱线称为巴耳末系
§20.4 氢原子光谱 玻尔的氢原子理论 原子量子理论概述: 1897 年发现电子并确认电子是原子的组成粒子 1900 年普朗克第一次提出量子假说 1905 年爱因斯坦提出光量子假说 不久汤姆逊最早提出一个原子结构模型 1911 年卢瑟福提出原子有核模型 1913 年玻尔根据卢瑟福的原子有核模型以及原子光谱的规律性,提出氢原子的量子 理论,初步奠定了原子物理学的基础 1924 年德布罗意提出实物粒子(如电子)与光子一样,也具有波-粒二象性假说 之后在此基础上,薛定谔、海森伯等人建立了新的量子力学。量子力学的建立标志 着人类对物质结构的认识有了新的突破。 从 1927 年开始量子力学用于固体物理领域,从而促进了对固体材料、半导体、激光、 超导等的研究。 一、氢原子光谱的规律性 1.光谱 研究原子结构的重要途径之一,是电磁辐射的波长成分和强度分布的记录。光谱可分 为三类:1.线状光谱 2.带状光谱 3.连续光谱 另还可分为发射和吸收光谱。 2.氢原子光谱 1885 年从某些星体的光谱中已观测氢谱线已达 14 条,瑞士科学家巴耳末发现有简单 规律: 0 2 2 B 3645.6A n 3,4,5, 4 = = − = 其中 n n B 称为巴耳末公式。 所对应的一组谱线称为巴耳末系

当n→m,元n→B,元-元n→0 令P一员称为波数 儿安中 其中R=1.0967758*107m-1称为氢原子的里德伯常数 「1 赖曼系: n=23,4, 巴耳末系:=R2 n=3,4,5 帕邢系: 17 =R 「1 n=4,5,6. n-5,6,7. 普丰特系:=R5 1 11 n=6,7,8 [司 n234) fK=1,23. =T(K)-T(m) 称为里兹合并原理 Ta)称为光诗项。氯原子光游项7网-是 n=1,2,3 氢原子光谱总结为三条特点: (1)线光谱,谱线位置确定,且彼此分立: (2)谱线间有一定关系: (a)谱线构成各谱线系: (b)不同系的谱线有关系。 (3)每一谱线的波数都可以表达为二光谱项之差。 二、玻尔氢原子理论 1.经典理论的困难
当 n → , n → B, n-1 − n → 0 令 ~ 1 = 称为波数 ) 1 2 1 ) ( 1 2 1 ( ~ 1 1 4 4 2 2 2 2 2 2 n R n B n n B = − = H − − = = 其中 RH=1.0967758*107m-1 称为氢原子的里德伯常数 称为里兹合并原理 ( ) , 普丰特系: , 布喇开系: , 帕邢系: , 巴耳末系: 赖曼系: ( ) ( ) ~ n 2,3,4, K 1 2 3 ~ 1 1 n 6 7 8 1 5 ~ 1 n 5 6 7 1 4 ~ 1 n 4,5 6 1 3 ~ 1 n 3,4,5 1 2 ~ 1 n 2,3,4, 1 1 ~ 1 2 2 2 2 2 2 2 2 2 2 2 2 T K T n K n K n R n R n R n R n R n R H H H H H H = − = = = − = = − = = − = = − = = − = = − T(n)称为光谱项。氢原子光谱项 ( ) = 2 n =1,2,3 n R T n H 氢原子光谱总结为三条特点: (1)线光谱,谱线位置确定,且彼此分立; (2)谱线间有一定关系: (a)谱线构成各谱线系; (b)不同系的谱线有关系。 (3)每一谱线的波数都可以表达为二光谱项之差。 二、玻尔氢原子理论 1.经典理论的困难

1911年卢瑟福在▣粒子散射实验基础上提出有核模型 电子绕核运动 m月 认为核不动,势能:U=K- 1e2 ,K是无穷远处的势能,若取K=0,则 1e2 U-4R6o r ② 由①②得原子的能量 1e2 1e2 0洛装释为。左 电子存在加速度,应该有连续电磁辐射 经典理论的困难: (1)由于原子连续辐射能量,电子能量下降,半径会减小,最后落到原子核上 (2)原子光谱应是连续谱 2.玻尔氢原子理论(1913年) (1)玻尔的基本假设: (a)定态假设: 电子的轨道和能量是量子化的,处于这些状态的电子不辐射能量,称为定态:,。 (b)量子跃迁假设: 当电子从能量较高定态E跃迁到另一能量较低的定态B时,辐射的光子能量hv=E。-Ek 反之吸收频率为Vm的光子: (c)轨道角动量量子化假设: 处于定态的电子,轨道角动量(动量矩:L=名=Mn=123.移为量子数 (2)玻尔理论的成就
1911 年卢瑟福在α粒子散射实验基础上提出有核模型 电子绕核运动 4 1 2 2 0 2 r e r v m = ① 认为核不动,势能: r e U K 2 4 0 1 = − ,K 是无穷远处的势能,若取 K=0,则 r e U 2 4 0 1 = − ② 由①②得原子的能量 r e r e E mv 4 2 1 4 1 2 1 2 0 2 0 2 = − = − 由①得频率为: 3 4 0 1 2 2 mr e r v = = 电子存在加速度,应该有连续电磁辐射 经典理论的困难: (1)由于原子连续辐射能量,电子能量下降,半径会减小,最后落到原子核上 (2)原子光谱应是连续谱 2.玻尔氢原子理论(1913 年) (1)玻尔的基本假设: (a)定态假设: 电子的轨道和能量是量子化的,处于这些状态的电子不辐射能量,称为定态:r1,r2,.rn (b)量子跃迁假设: 当电子从能量较高定态 En跃迁到另一能量较低的定态 Ek时,辐射的光子能量 hνkn=En-Ek 反之吸收频率为 νkn 的光子; (c)轨道角动量量子化假设: 处于定态的电子,轨道角动量(动量矩): n 1,2,3,称为量子数 2 = = n = h L n (2)玻尔理论的成就

设原子核静止,则: mvr=nh v21e2 m =4nn n=1,2, me 可见,轨道半径只能取一系列分立值。 对应n1称为基态,半径=4红G=0529×10”m=0529A称为玻尔半径. me 1e2 E=4x62 么-切 me? me 1 得E.=8GF 当,对应基态能量为:么218x10"=-136@ 其他定态的能量为 hvu En-Ex %华,成告- 1 me411 →元-8cmc定7 me2 R,=8ch。=1.0973731x10'm 以上与实验符合得很好。 三、玻尔氢原子理论改进及其局限 §20.5德布罗意波波-粒二象性 一、德布罗意波(1924年)
设原子核静止,则: n 1,2, 4 4 1 2 2 2 0 2 2 0 2 = = = = me n r r e r v m mvr n n 可见,轨道半径只能取一系列分立值。 对应 n=1 称为基态,半径 0.529 10 0.529 称为玻尔半径 4 0 10 2 2 0 1 m A me r = = = − 。 2 2 2 0 4 2 2 2 0 2 0 1 8 4 4 2 1 h n me E me n r r e E n n = − = = − 得 由 当 n=1,对应基态能量为: J eV h n me E 2.18 10 13.6 1 8 18 2 2 2 0 4 1 = = − = − − 其他定态的能量为 7 1 2 3 0 2 2 3 2 2 0 4 kn kn 2 1.0973731 10 8 ) 1 1 ( 8 ~ ( ) ~ 1 , ( ) (n 1) 13.6 − = = = − = = = − = − = − m h c me R h c k n me E E h c hc E E h E E eV n E H n k n k kn kn kn n k n 以上与实验符合得很好。 三、玻尔氢原子理论改进及其局限 §20.5 德布罗意波 波-粒二象性 一、德布罗意波(1924 年)