
第四篇 胶家颇

第于五意 机威垢 挑羰振 阻尼振动受迫振动共振
阻尼振动受迫振动共振
§15-1机械振动的一般概念 机械振动:物 体在一定位置的 附近作来回往复 的运动(周期性 或非周期性) ▣成因:物体的惯性和所受的回复力
§15-1 机械振动的一般概念 机械振动:物 体在一定位置的 附近作来回往复 的运动(周期性 或非周期性) 成因:物体的惯性和所受的回复力
§15-2 简谐振动 一.简谐振动的特征 口简谐振动:物体距平衡位 置的位移(或角位移)随时 间按余弦(或正弦)函数变 化
简谐振动:物体距平衡位 置的位移(或角位移)随时 间按余弦(或正弦)函数变 化 §15-2 简谐振动 一 .简谐振动的特征

1.动力学特征 F=0 口胡克定律:物体所 w- 受弹性力与物体的 位移成正比而反向 即F=-kx 简谐振动的动力学特征 2.运动学特征 'F=m d'x =一kx 令02 dt" 三
1.动力学特征 F = −kx 0 x m 胡克定律:物体所 受弹性力与物体的 位移成正比而反向 即 -简谐振动的动力学特征 F = 0 x m 0 F 2.运动学特征 2 2 dt d x F = m = −kx m k = 2 令

d"x +02x=0 位移 x=Acos(ot+) -一简谐振动表达式 速度 dx V= =-@Asin(ot+p) -V sin(ot+p〉 加速度 d"x dt2 =-@2Acos(ot+p -a cos(wt+p)
0 2 2 2 + x = dt d x 速度 dt dx v = = −v sin(t +) m 位移 x = Acos(t +) -简谐振动表达式 = −Asin(t +) 加速度 2 2 dt d x a = cos( ) 2 = − A t + = −a cos(t +) m

即有a=-02x 一简谐振动的运动学特征 说明: A-简谐振动的振幅,为物体离开 平衡位置最大位移的绝对值 0-圆频率(2元秒内的振动次数) 0t+0-简谐振动的相位 简谐振动的初相位
即有 a x 2 = − -简谐振动的运动学特征 说明: -简谐振动的振幅,为物体离开 平衡位置最大位移的绝对值 -简谐振动的初相位 t +-简谐振动的相位 A -圆频率(2秒内的振动次数)

讨论: 由初始条件可确定A和o: 设t=0时,x=x,V=0 .o=Acos vo =-@Asin o 可得 A=1 =arcig
讨论: 由初始条件可确定A和 : 设 t =0 时, x0 = Acos v0 = −Asin 2 0 2 0 = + v A x = − 0 0 x v arctg 0 x = x 0 v = v 可得

固有频率和固有周期: m .T= 2π 2 m T 2元 m -周期和频率由振动系统本身 的性质所决定,与A和无关
固有频率和固有周期: -周期和频率由振动系统本身 的性质所决定,与A和无关 m k = 2 T = k m = 2 T 1 = m k 2 1 =
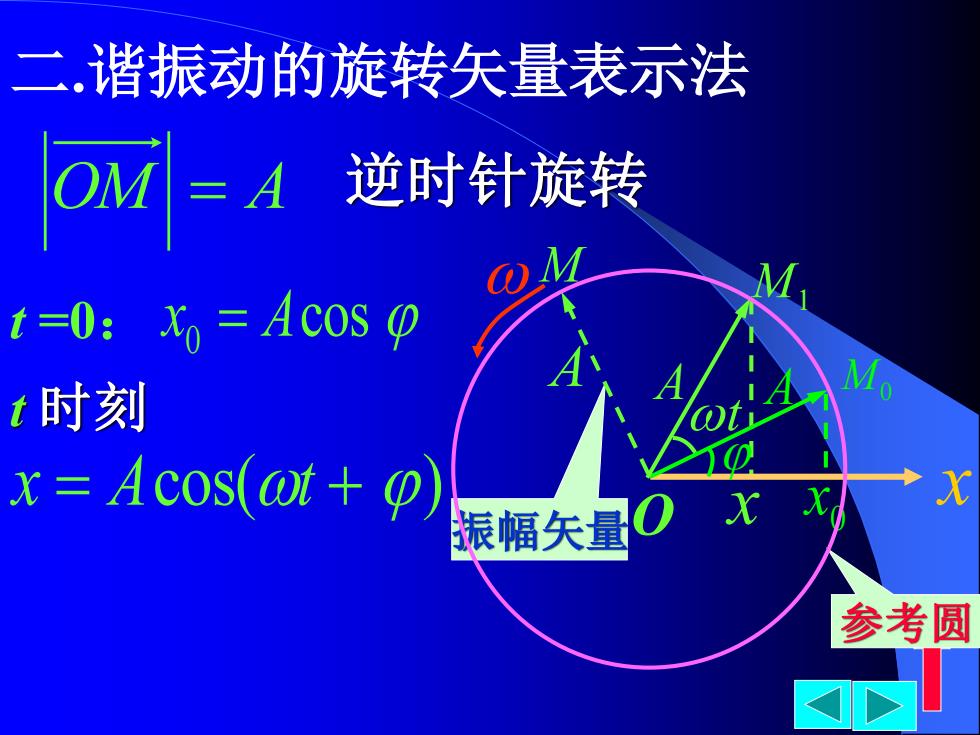
二.谐振动的旋转矢量表示法 OM=A逆时针旋转 t=0: =Acos t时刻 x=Acos(at+p) 振幅矢量O 参考圆
二.谐振动的旋转矢量表示法 0 x x x A M0 M1 t A OM = A t =0: x0 = Acos t 时刻 x = Acos(t + ) 参考圆 振幅矢量 逆时针旋转 O A M