
石河子大学实验范学院物理系】 近代物理实验讲义 费米-狄拉克分布 【实验目的】 1.通过实验验证费米一狄拉克分布。 2.学习一种实验方法及处理实验数据的技巧。 【实验器材】 M-Ⅱ型费米-狄拉克分布实验仪 【实验原理】 近代电子理论认为金属中的电子按能量的分布是遵从费米一狄拉克的量子统计规律的, 费米分布函数为 8e)=eple-8)/k]+7 (1) 金属中的每个电子都占有一定能量的能级,这些能级相互靠得很近,形成能带。当其温 度为绝对零度时,金属中电子的平均能量并不为零。此时金属中的电子将能量从零到能量ε, (8,称费米能级,£,的值随金属的不同而不同)的能级全部占据。而高于费米能级的那些 能级全部空着,没有电子去占据。如图(1)中的实线所示,当金属的温度为1500℃,则靠 近费米能级的少数电子由于运动的加剧,其能量超过ε,值,因而从低于费米能级的能带跃 迁到高于费米能级的能带上去,其分布曲线如图(1)中虚线所示。我们的实验是在灯丝灼 热(约1400℃-1500'C)的情况下进行的,因此我们实验所测的结果也只是靠近费米能级的 一部分,如图(1)中矩形所包的虚线部分。 对(1)式求导可得 &e)=$ -expl(6-6)/kT] ds kTfexpl(-5)/kT]+ (2) (1)、(2)两式的理论曲线如图(1)和图(2)所示
石河子大学实验范学院物理系 近代物理实验讲义 费米-狄拉克分布 【实验目的】 1.通过实验验证费米—狄拉克分布。 2.学习一种实验方法及处理实验数据的技巧。 【实验器材】 FM-Ⅱ型费米-狄拉克分布实验仪 【实验原理】 近代电子理论认为金属中的电子按能量的分布是遵从费米—狄拉克的量子统计规律的, 费米分布函数为 exp kT 1 1 g − f + = [( )/ ] ( ) ε ε ε (1) 金属中的每个电子都占有一定能量的能级,这些能级相互靠得很近,形成能带。当其温 度为绝对零度时,金属中电子的平均能量并不为零。此时金属中的电子将能量从零到能量 f ε ( f ε 称费米能级, f ε 的值随金属的不同而不同)的能级全部占据。而高于费米能级的那些 能级全部空着,没有电子去占据。如图(1)中的实线所示,当金属的温度为 15000 C,则靠 近费米能级的少数电子由于运动的加剧,其能量超过 f ε 值,因而从低于费米能级的能带跃 迁到高于费米能级的能带上去,其分布曲线如图(1)中虚线所示。我们的实验是在灯丝灼 热(约 14000 C~15000 C)的情况下进行的,因此我们实验所测的结果也只是靠近费米能级的 一部分,如图(1)中矩形所包的虚线部分。 对(1)式求导可得 2 f f kT exp kT 1 exp kT d dg g { [( )/ ] } ( ) [( )/ ] ( ) − + − − = = ε ε ε ε ε ε ε (2) (1)、(2)两式的理论曲线如图(1)和图(2)所示。 1

石河子大学实验范学院物理系 近代物理实验讲义 由于金属内部电子的能量无法测量,只能对真空中热发射电子的动能分布进行测量。由 于电子在真空中的热运动与电子在金属内部的运动情况完全不同,这是因为金属内部存在者 带正电的原子核,电子不但有热运动的动能,而且还具有势能,真空中的电子就不存在势能, £,=0,还要消耗一部分能量用作逸出功,因此从金属内部电子的能量ε减去逸出功A,就 可得到真空中热发射电子的动能: 6=6-A (3) 此外,在真空与金属表面附近还存在着电子气形成的偶电层,就是说迷出金属表面的电 子,还要消耗一些能量穿越偶电层,根据前苏联科学院院士,符伦克尔和塔姆的理论,电子 穿越偶电层所需要的能量,也就是该金属的费米能级,·考虑到这两个因素之后对费米函 数作适当的修正是非常必要的,修正后的费米函数应为: g(e)= expl(Ex-E)/KT]+1 (4) 对(4)式求导得 86)=$(e -exp((Ex-E1)/KT] de,KTexp(6)/KT]+ (5) 由(4)、(5)两式可以看出,真空中发射电子的动能分布也遵从费米一狄拉克分布。 【实验方法及数据处理】 本实验是利用理想二极管的特殊结构,在管子的外面套一个螺线管,并且通以直流电流, 则螺线管中的磁感应强度B的方向与光子的轴线(灯丝)平行,在二极管不加板压的情况 下(山。=0),从灯丝发射出电子,沿半径方向飞向圆柱面板级(阳极),由于阳板电压为 零,所以电子在不受外电场力的作用下,保持其初动能飞向阳极形成阳极饱和电流,其线路 如图(3)所示。 图(3)
石河子大学实验范学院物理系 近代物理实验讲义 由于金属内部电子的能量无法测量,只能对真空中热发射电子的动能分布进行测量。由 于电子在真空中的热运动与电子在金属内部的运动情况完全不同,这是因为金属内部存在着 带正电的原子核,电子不但有热运动的动能,而且还具有势能,真空中的电子就不存在势能, f ε =0,还要消耗一部分能量用作逸出功,因此从金属内部电子的能量ε 减去逸出功 A,就 可得到真空中热发射电子的动能 k ε ε k = ε − A (3) 此外,在真空与金属表面附近还存在着电子气形成的偶电层,就是说逃出金属表面的电 子,还要消耗一些能量穿越偶电层,根据前苏联科学院院士,符伦克尔和塔姆的理论,电子 穿越偶电层所需要的能量,也就是该金属的费米能级 f ε 。考虑到这两个因素之后对费米函 数作适当的修正是非常必要的,修正后的费米函数应为: exp kT 1 1 g k f k − + = [( )/ ] ( ) ε ε ε (4) 对(4)式 求导得 2 k f k f k k k kT exp kT 1 exp kT d dg g { [( )/ ] } ( ) [( )/ ] ( ) − + − − = = ε ε ε ε ε ε ε (5) 由(4)、(5)两式可以看出,真空中发射电子的动能分布也遵从费米—狄拉克分布。 【实验方法及数据处理】 本实验是利用理想二极管的特殊结构,在管子的外面套一个螺线管,并且通以直流电流, 则螺线管中的磁感应强度 B 的方向与光子的轴线(灯丝)平行,在二极管不加板压的情况 下( ),从灯丝发射出电子,沿半径方向飞向圆柱面板级(阳极),由于阳板电压为 零,所以电子在不受外电场力的作用下,保持其初动能飞向阳极形成阳极饱和电流,其线路 如图(3)所示。 u p = 0 2

石河子大学实验范学院物理系 近代物理实验讲义 由于电子的初动能各不相同,如何将它们按相等的动能间隔区分开来,并且求出电子数 目的相对值,便成为本实验的焦点。由图(4)可知,从二极管灯丝(即圆心)发射出的电 子,沿半径方向飞向圆柱面阳极(即圆周),在螺线管所产生的磁感应强度B的作用下,电 子将受到洛仑兹力F=一v×B而作匀速圆周运动。洛仑兹力是向心力,它不改变电子的动 能,由于v⊥B,所以洛仑兹力公式可用下式表示: 十 阳极 灯然 图4 fi=Bey=m (6) R v=BeR (7) (7)式中的是电子沿二极管半径方向的速度:或者电子的速度在半径方向的分量, R是电子作匀速圆周运动的半径,m是电子的质量,B是螺线管中间部分的磁感应强度,B 的计算公式为: oNIa B-D (8) (8)式中,4,=4π×10-(HWm)是真空中的磁导率:N是螺线管的总匝数:L和D 分别是螺线管的长度和直径,1®是通过螺线管的电流强度。将(7)、(8)代入(6)式可得 真空中电子的动能为: (9)
石河子大学实验范学院物理系 近代物理实验讲义 3 由于电子的初动能各不相同,如何将它们按相等的动能间隔区分开来,并且求出电子数 目的相对值,便成为本实验的焦点。由图(4)可知,从二极管灯丝(即圆心)发射出的电 子,沿半径方向飞向圆柱面阳极(即圆周),在螺线管所产生的磁感应强度 B 的作用下,电 子将受到洛仑兹力 而作匀速圆周运动。洛仑兹力是向心力,它不改变电子的动 能,由于 ,所以洛仑兹力公式可用下式表示: F = −ev× B v ⊥ B R mv f Bev 2 L = = (6) m BeR v = (7) (7)式中的 v 是电子沿二极管半径方向的速度;或者电子的速度在半径方向的分量, R 是电子作匀速圆周运动的半径,m 是电子的质量,B 是螺线管中间部分的磁感应强度,B 的计算公式为: 2 2 0 B L D NI B + = µ (8) (8)式中, (H/m)是真空中的磁导率;N是螺线管的总匝数;L和D 分别是螺线管的长度和直径,I 7 0 4 10 − µ = π × B是通过螺线管的电流强度。将(7)、(8)代入(6)式可得 真空中电子的动能为: 2 B 2 2 2 2 2 2 2 0 K I m e 2 L D m N R mv 2 1 ( ) + = = µ ε (9)

石河子大学实验范学院物理系 近代物理实验讲义 由(4)可看出,若电子作匀速圆周运动的半径号(日是圆柱面阳极的直径,电子就 能达到阳极,形成阳极电流,若R(日,电子就不能到达阳极,这一部分电子对阳极电流无 页就。可见电子作匀落圆周运动的半径(取决于。直接影响闲极电流的大小,将风-号代 入(9)式可得 Ek =KIg (10) (10)式中 Ky 为一常数,由(10)式可知真空中发射电子的动能与螺线管中的电流强度的平方成正比, 而洛仑兹力不改变电子的动能,它只影响电子作匀速圆周运动的半径的大小,对动能一定的 电子,向心力越大(即I后越大)匀速圆周运动的半径越小,当动能增加△x时,将有相应 数最的电子因其圈周运动的半径小于而不能达到阳极,所以阳极电流将减小△,又因 为△5x与后成正比,所以可用后代替变量6x进行实验及数据处理。 实验中,设灯丝电流强度稳定不变,阳极电压为零,理想二极管的饱和电流为: IP。-noe (11) (11)式中的n,以及下面的n;n2;n3均为单位时间内到达阳极的电子数目,当I后以 相等的改变量依次增加下去,我们将得到一组方程: IP =nje IP,=n,e (12) , 由(11)、(12)式联立可得 △R=IP,-IR,=(n-n)e=△n,e △P=P-P=(n,-m)e=△n,e (13) IP:IP =n no (12) P,/P。=n,/nn (14) △P,/IP,=△n,In, △P/IP=△n,/no (15) 为了配合理论上的要求,操作时事先选好后的值,使其等间隔的增加,然后以其平方 根的值,作为实验测量时的电流值,进行实际测试
石河子大学实验范学院物理系 近代物理实验讲义 4 由(4)可看出,若电子作匀速圆周运动的半径 4 d R〉 (d是圆柱面阳极的直径),电子就 能达到阳极,形成阳极电流,若 4 d R〈 ,电子就不能到达阳极,这一部分电子对阳极电流无 贡献。可见电子作匀速圆周运动的半径(取决于IB)直接影响阳极电流的大小,将 4 d R = 代 入(9)式可得 (10) 2 K = KI B ε (10)式中 2 2 2 2 14 2 2 m e 2 L D 10 N d m K ( ) ( + ) × = − π 为一常数,由(10)式可知真空中发射电子的动能与螺线管中的电流强度的平方成正比, 而洛仑兹力不改变电子的动能,它只影响电子作匀速圆周运动的半径的大小,对动能一定的 电子,向心力越大(即 越大)匀速圆周运动的半径越小,当动能增加 2 B I K ∆ε 时,将有相应 数量的电子因其圆周运动的半径小于 4 d 而不能达到阳极,所以阳极电流将减小 ,又因 为 p ∆I K ∆ε 与 成正比,所以可用 代替变量 2 B I 2 B I K ε 进行实验及数据处理。 实验中,设灯丝电流强度稳定不变,阳极电压为零,理想二极管的饱和电流为: IP n e 0 = 0 (11) (11)式中的 以及下面的 均为单位时间内到达阳极的电子数目,当 以 相等的改变量依次增加下去,我们将得到一组方程: n0 n1 ;n2 ;n3 ;K 2 B I ⎪ ⎭ ⎪ ⎬ ⎫ = = LL IP n e IP n e 2 2 1 1 (12) 由(11)、(12)式联立可得 ⎪ ⎭ ⎪ ⎬ ⎫ ∆ = − = − = ∆ ∆ = − = − = ∆ LL IP IP IP n n e n e IP IP IP n n e n e 2 1 2 1 2 2 1 0 1 0 1 1 ( ) ( ) (13) ( ) ( ) 11 12 得 (14) ⎪ ⎭ ⎪ ⎬ ⎫ = = LL 2 0 2 0 1 0 1 0 IP IP n n IP IP n n / / / / ( ) ( ) 11 13 得 (15) ⎪ ⎭ ⎪ ⎬ ⎫ ∆ = ∆ ∆ = ∆ LL 2 0 2 0 1 0 1 0 IP IP n n IP IP n n / / / / 为了配合理论上的要求,操作时事先选好 的值,使其等间隔的增加,然后以其平方 根的值,作为实验测量时的电流值,进行实际测试。 2 B I

石河子大学实验范学院物理系 近代物理实验讲义 【数据记录】 1螺线管的总匝数 N= 2螺线管的长度 m 3螺线管的平均直径D m 4.真空中的磁导率 46=4πx10-7(H1m) 5.圆柱面极的直径d8.4mm(用测量显微镜测) (1)以P1P,为y轴,以1后为x轴,作g(sx)~Ex曲线。 (2)以△P/IP,为y轴,以I后为x轴,作g(ex)~Ex曲线 (3)求∑=识,检查是香满足归一化条件。 P (4)计算g(6g)~6x曲线峰值对应的6x值即为5值, 【分析讨论】
石河子大学实验范学院物理系 近代物理实验讲义 5 【数据记录】 1.螺线管的总匝数 N= 2.螺线管的长度 L= m 3.螺线管的平均直径 D= m 4.真空中的磁导率 4 10 (H / m) 7 0 − µ = π × 5.圆柱面极的直径 d=8.4mm(用测量显微镜测) (1)以 IPi / IP0 为 y 轴,以 为 x 轴,作 2 B I K K g(ε ) ~ ε 曲线。 (2)以∆IPi / IP0 为 y 轴,以 为 x 轴,作 曲线。 2 B I K K ' g (ε ) ~ ε (3)求∑ ∆ = 0 i IP IP ,检查是否满足归一化条件。 (4)计算 K K 曲线峰值对应的 ' g (ε ) ~ ε K ε 值即为 f ε 值。 【分析讨论】
石河子大学实验范学院物理系】 近代物理实验讲义 090 10 0650 550 000. 0t8.0 0-60 0210 000 00( 编者:高艳
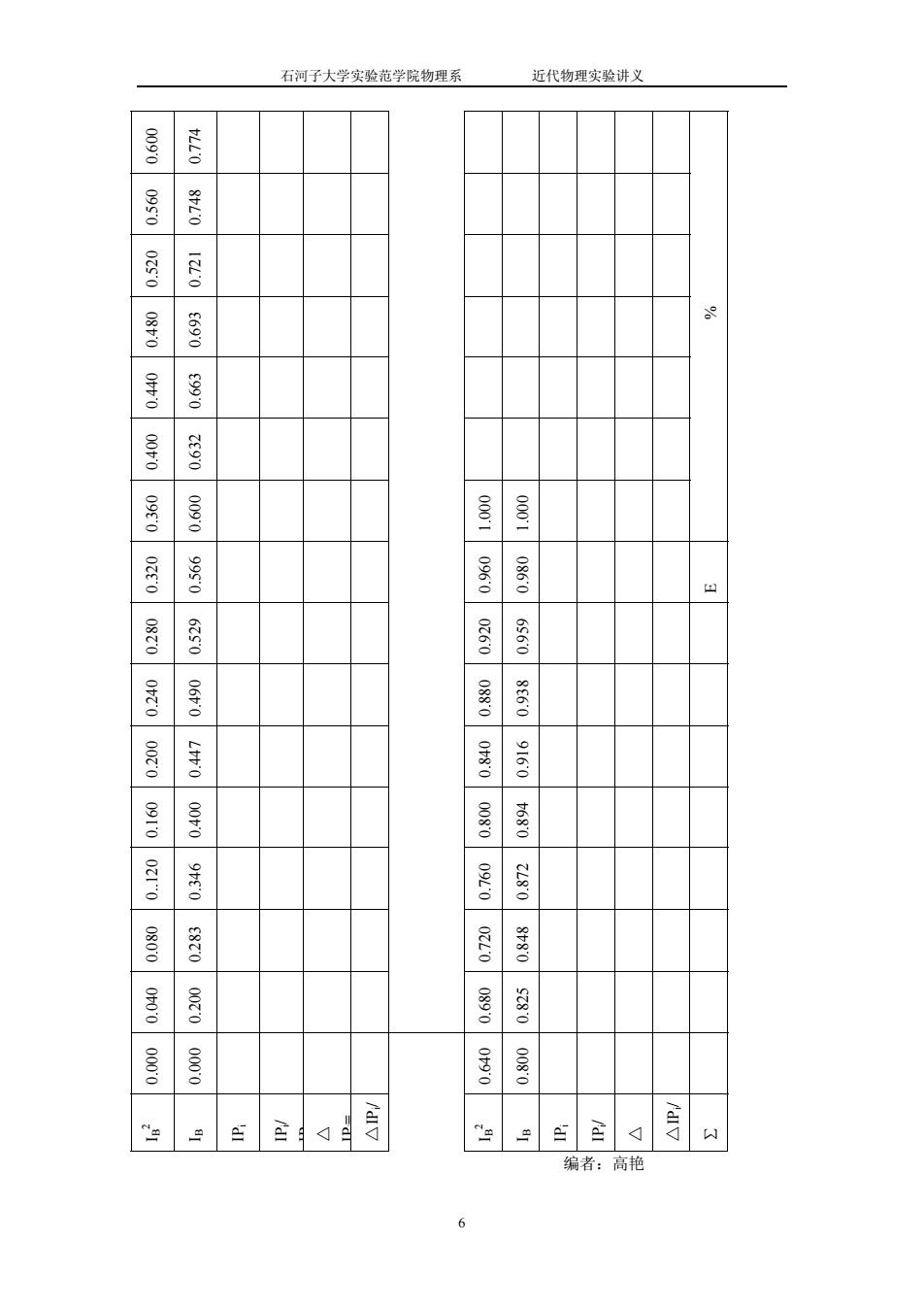
石河子大学实验范学院物理系 近代物理实验讲义 6 0.600 0.774 0.560 0.748 0.520 0.721 0.480 0.693 0.440 0.663 0.400 0.632 0.360 0.600 1.000 1.000 % 0.320 0.566 0.960 0.980 E 0.280 0.529 0.920 0.959 0.240 0.490 0.880 0.938 0.200 0.447 0.840 0.916 0.160 0.400 0.800 0.894 0.120 0.346 0.760 0.872 0.080 0.283 0.720 0.848 0.040 0.200 0.680 0.825 0.000 0.000 0.640 0.800 IB 2 IB IPi IPi/ IP △ IP =i △IPi/ IB 2 IB IPi IPi/ △ △IPi/ ∑ 编者:高艳