
第三篇气体分子运动和热力学基础 1、研究对象 热现象及其运动规律 2、研究方法 气体分子运动论研究微观本质,热力学研究宏观规律,两者的方法不同,相 辅相成 第六章气体动理论 §6一1、2、3理想气体的宏观与微观描述 一、宏观:平衡态状态参量(P、V、T) T=C(气体质量一定) PV N-总T=Is3K,者适气体8爱》 描述参量有几何参量、力学、化学和电磁学四种常用的参量。 二、微观:大量分子组成 (1)全同粒子 (2)每个粒子运动适从牛顿定律 (3)总数大,遵从统计规律: (4)体积可忽略(由气体到固体,体积缩小1000倍,分子间平均距离是其 线度的√000=10倍): (5)一般情况下自由的(分子间作用距离缩小,大多数时间内分子间距离 较其作用距离大很多): (6)弹性碰撞,时间不计(作用力是保守力,且作用时间很短)。 三、压强公式
第三篇 气体分子运动和热力学基础 1、研究对象 热现象及其运动规律 2、研究方法 气体分子运动论研究微观本质,热力学研究宏观规律,两者的方法不同,相 辅相成。 第六章 气体动理论 §6-1、2、3 理想气体的宏观与微观描述 一、宏观:平衡态状态参量(P、V、T) C T PV = (气体质量一定) RT RT M M PV mol = = (R=8.31Jmol-1K-1,普适气体常数) 描述参量有几何参量、力学、化学和电磁学四种常用的参量。 二、微观:大量分子组成 (1)全同粒子; (2)每个粒子运动适从牛顿定律; (3)总数大,遵从统计规律; (4)体积可忽略(由气体到固体,体积缩小 1000 倍,分子间平均距离是其 线度的 1000 = 10 倍); (5)一般情况下自由的(分子间作用距离缩小,大多数时间内分子间距离 较其作用距离大很多); (6)弹性碰撞,时间不计(作用力是保守力,且作用时间很短)。 三、压强公式

P-in 其中是单位体积内的分子数,。是分子的平均平动动能。 推导:如图设山以内有N个分子,质量为m。 1、大量分子遵从统计规律 Vξ=V=v -g+0灭=g.四- A 0-mV 2、某个分子与A:碰一次,冲量为2mVx(弹性碰撞),到达A后来回一次时间为 头,则米个分子单位时间与A的碰撞次数为六 2L,1 所以华位时间作用在A的冲显为2mV2元 1 3、大量分子 按定义 F m 含沙品器m网 →p=gmv 故P=no 注意: (1)推导过程体现了分子物理的研究方法一一统计规律(不是力学规律): (2)没有考虑分子与分子之间的碰撞,但不影响结果: (3)公式本身不能直接证明,但可以解释和推导出很多实验定律。 四、几个有用的公式和推论 1、P=kT阿伏加德罗定律
= n 3 2 P 其中 n 是单位体积内的分子数, 是分子的平均平动动能。 推导:如图设 1 2 3 l l l 内有 N 个分子,质量为 m。 1、大量分子遵从统计规律 2 2 z 2 y 2 x 2 z 2 y 2 x 2 2 z 2 y 2 x V 3 1 V V V V V V V V V V = = = = + + = = 2 mV 2 1 = 2、某个分子与 A1 碰一次,冲量为 2mVx(弹性碰撞),到达 A2 后来回一次时间为 x 1 V 2L ,则某个分子单位时间与 A1 的碰撞次数为 1 x 2L V 。 所以单位时间作用在 A1 的冲量为 1 2 x 1 x x mV 2L V 2mV = 。 3、大量分子 = = = = = N i 1 N i 1 2 ix 1 1 2 ix dt dP V F L m L mV F 按定义 2 2 x N i i 2 i x 1 2 3 N i i 2 i x 2 3 1 2 3 nmV 3 1 P nmV N V L L L Nm V L L L m L L F P = = = = = = = 故 = n 3 2 P 注意: (1)推导过程体现了分子物理的研究方法——统计规律(不是力学规律); (2)没有考虑分子与分子之间的碰撞,但不影响结果; (3)公式本身不能直接证明,但可以解释和推导出很多实验定律。 四、几个有用的公式和推论 1、P=nkT 阿伏加德罗定律

ow-k P总g是=灯 k-尽-138x0K波尔签曼指数 例:一容器内储有气体,温度为27℃。问:(1)压强为1.013×10Pa时, 在1m3中有多少个分子:(2)在高真空时,压强为1.33×105Pa,在1m中有多 少个分子? 解:按公式P=kT可知, 1.013×105 (1)n=际138×10x30m3=245x10m 2)n-导F580x0m=321k10m 1.33×105 可以看出,两者相差100倍。 P>卫,T1≈T。 AN=BY-10x102×133×102112×10 573 138x10=1.8x10"个 2、由 3 P=nkT 而一摩尔分子)MV=RT 注意: (1)指出温度德真实含义,说明绝对零度不可能达到: (2)V2关于参照系的问题(分子的质心系):
RT M M PV mol = T nkT N R V N V RT M M P mol = = = 23 1 1.38 10 J K N R k − − = = ,波尔兹曼常数 例:一容器内储有气体,温度为 27℃。问:(1)压强为 1.013×105Pa 时, 在 1m3 中有多少个分子;(2)在高真空时,压强为 1.33×10-5Pa,在 1m3 中有多 少个分子? 解:按公式 P=nkT 可知, (1) 3 25 3 23 5 m 2.45 10 m 1.38 10 300 1.013 10 kT P n − − − = = = (2) 3 15 3 23 5 m 3.21 10 m 1.38 10 300 1.33 10 kT P n − − − − = = = 可以看出,两者相差 1010 倍。 k V ) T P T P )V ( kT P kT P N (n n )V ( 1 1 1 1 1 = − = − = − T T P P , 1 1 18 23 2 2 3 1 1 1.88 10 1.38 10 11.2 10 573 1.0 10 1.33 10 k V T P N = = − − − 个 2、由 mV ) 2 1 ( 2kT 3 P nkT n 3 2 P 2 = = = = (每个分子) 而一摩尔分子 RT 2 3 M V 2 1 2 mol = 注意: (1)指出温度德真实含义,说明绝对零度不可能达到; (2) 2 V 关于参照系的问题(分子的质心系);

(3)可得出均方根速率 臣哥 例:试求氮气分子的平均平动动能和方均根速率,设(1)在温度t=1000℃ 时,(2)在温度t=0℃时,(3)在温度t=一150℃时。 解:(1)1000℃时, 0=2kT-3x138×10-×12731=263×10y F-思。wa: (2)同理,在t=0℃时, 0=kT=号x138×10-4×2731=565×10-J 际恶 2m/s=493m/s (3)在温度t=-150℃时, 0=2kT=2×1.38×10-2×123=255×10-2 =V28×10 3、迈耳顿分压定律 设有n种不同的气体混合储存在同一容器中,温度相同, a-kT0=0-=0 设单位体积含各种气体的分子数分别为、2、. 则单位体积总分子数n=n+n,+ p-号no号a+n+g-号n回+号n,o+ →P=P+P2+. 其中R=n,B=子n,.,为积分压强。 混合气体的压强等于组成混合气体的各成份的分压强之和
(3)可得出均方根速率 mol 2 2 M 3kT m 3kT mV V 2 1 kT 2 3 = = = = 例:试求氮气分子的平均平动动能和方均根速率,设(1)在温度 t=1000℃ 时,(2)在温度 t=0℃时,(3)在温度 t=-150℃时。 解:(1)1000℃时, 1.38 10 1273J 2.63 10 J 2 3 kT 2 3 −23 −20 = = = m/s 1.06 10 m/s 28 10 3 8.31 1273 M 3kT V 3 3 mol 2 = = = − (2)同理,在 t=0℃时, 1.38 10 273J 5.65 10 J 2 3 kT 2 3 −23 −21 = = = m/s 493m/s 28 10 3 8.31 273 M 3kT V 3 mol 2 = = = − (3)在温度 t=-150℃时, 1.38 10 123J 2.55 10 J 2 3 kT 2 3 −23 −21 = = = m/s 331m/s 28 10 3 8.31 123 M 3kT V 3 mol 2 = = = − 3、迈耳顿分压定律 设有 n 种不同的气体混合储存在同一容器中,温度相同, = kT 1 = 2 = = 2 3 设单位体积含各种气体的分子数分别为 n1、n2、. 则单位体积总分子数 n = n1 + n2 + = = 1 + 2 + = 11 + n 22 + 3 2 n 3 2 (n n ) 3 2 n 3 2 P P = P1 + P2 + 其中 1 n1 1 3 2 P = , 2 n2 2 3 2 P = ,. ,为积分压强。 混合气体的压强等于组成混合气体的各成份的分压强之和

§6一4能均分原理(定理),理想气体的内能 一、自由度:决定一个物体的位置所需要的独立坐标数 (1)自由运动的质点有3个自由度(平动,X、Y、Z): (2)自由运动的刚体有6个自由度(3个平动,3个转动): 点X、Y、Z,方位角a、B、Y,cos2a+cos2B+cos2y=1 (3)当物体运动受到限制时,自由度数会减少: (4)分子的自由度: (a)单原子分子,3个 (b)双原子分子,3个平动,2个转动,1个振动,共6个(常温下5 个) (c)多原子分子(3个或3个以上原子组成的分子) 一般情况下,n个原子组成的分子,最多有3如个自由度。其中3个平动,3 个转动,其余3一6个为振动(运动受限制时,自由度减少)。 二、能均分原理 已知@=m7=kT,分子的平均平动能 分子有三个平动自由度X、Y、Z 而V2-V+V2+V好 mV-3mV:+mV:+mV: 且-V-V →mv-m=mv-o=k灯 根据经典统计力学的基本原理,将结论推广到分子的转动和振动 能均分原理:在温度为T的平衡态下,物质(气体,液体或固体)分子的 每一个自由度都具有相同的平均动能,其大小都等于)k灯。 如气体分子有1个自由度 i=t(平动)+r(转动)十s(振动) 则每个分子的平均总动能
§6-4 能均分原理(定理),理想气体的内能 一、自由度:决定一个物体的位置所需要的独立坐标数 (1)自由运动的质点有 3 个自由度(平动,X、Y、Z); (2)自由运动的刚体有 6 个自由度(3 个平动,3 个转动); 点 X、Y、Z,方位角α、β、γ,cos cos cos 1 2 2 2 + + = (3)当物体运动受到限制时,自由度数会减少; (4)分子的自由度; (a)单原子分子,3 个 (b)双原子分子,3 个平动,2 个转动,1 个振动,共 6 个(常温下 5 个) (c)多原子分子(3 个或 3 个以上原子组成的分子) 一般情况下,n 个原子组成的分子,最多有 3n 个自由度。其中 3 个平动,3 个转动,其余 3n-6 个为振动(运动受限制时,自由度减少)。 二、能均分原理 已知 kT 2 3 mV 2 1 2 = = ,分子的平均平动能 分子有三个平动自由度 X、Y、Z 而 2 z 2 y 2 x 2 V = V + V + V 2 z 2 y 2 x 2 mV 2 1 mV 2 1 mV 2 1 mV 2 1 = + + 且 2 2 z 2 y 2 x V 3 1 V = V = V = kT 2 1 3 1 mV 2 1 mV 2 1 mV 2 1 2 z 2 y 2 x = = = = 根据经典统计力学的基本原理,将结论推广到分子的转动和振动 能均分原理:在温度为 T 的平衡态下,物质(气体,液体或固体)分子的 每一个自由度都具有相同的平均动能,其大小都等于 kT 2 1 。 如气体分子有 I 个自由度 i = t(平动)+r(转动)+s(振动) 则每个分子的平均总动能

o=k灯=t+r+sk灯 上式的统计意义: (1)每个分子平均总动能相等 (2)每个自由度上的平均动能相等 每摩尔分子平均总动能 E.-N.0-RT 质量为M,摩尔质量为Mml的分子平均动能 三、理想气体的内能 内能概念: (1)分子热运动(平动、转动、振动): (2)分子间势能: (3)分子内能量: (4)原子核能。 注意: (1)气体的内能仅指气体分子热运动能和分子间势能: (2)对理想气体,只是指气体分子热运动能 由振动学知,振动在一个周期内的平均动能等于平均势能,所以每个振动自 由度除kT平均动能外,还有kT平均势能。 所以理想气体内能: 1个分子, E=7(t+r+s)kT 1摩尔分子, E.=t+r+2s)k灯 M质量分子, E-E-+r+a灯
(t r s)kT 2 1 kT 2 i = = + + 上式的统计意义: (1)每个分子平均总动能相等; (2)每个自由度上的平均动能相等。 每摩尔分子平均总动能 RT 2 i E = N = 质量为 M,摩尔质量为 Mmol 的分子平均动能 RT 2 i M M E M M E mol mol = = 三、理想气体的内能 内能概念: (1)分子热运动(平动、转动、振动); (2)分子间势能; (3)分子内能量; (4)原子核能。 注意: (1)气体的内能仅指气体分子热运动能和分子间势能; (2)对理想气体,只是指气体分子热运动能 由振动学知,振动在一个周期内的平均动能等于平均势能,所以每个振动自 由度除 kT 2 1 平均动能外,还有 kT 2 1 平均势能。 所以理想气体内能: 1 个分子, (t r s)kT 2 1 E = + + 1 摩尔分子, (t r 2s)kT 2 1 E = + + M 质量分子, (t r 2s)kT 2 1 M M E M M E mol mol = = + +

内能仅与自由度和温度有关,所以将“理想气体的内能只是温度的单值函数 作为理想气体的定义。 例:当温度为0℃时,分别求氢、氢、氧。氨、氯和二氧化碳等气体各1mol 的内能。温度升高K时,内能各增加多说?(双原子以上分子均视为刚性分子) 解:按题意,对单原子气体的分子按三个平动自由度计算分子的平均动能, 对双原子或多原子气体按六个自由度计算分子平均动能。按上述公式,1mol理 想气体的内能为 E=(t+r+2s)kT 可算出0C,即273K时,1mol理想气体的内能分别为 单原子气体 E=×831×273=341×10J 双原子气体: E=3×831x273=568x10J 三原子以上的气体: E=9×831x273=681x10 由Em=)(t+r+2s)kT可看到,当温度从T增加到T+△T时,内能量增加 为 AE-(t+r+2s)kAT 所以温度每升高1K时,1mol理想气体的内能增加,(t+r+2s)k, 单原子气体: AE-2x8311=25 双原子气体: AE=×831×1=20.8 三原子以上气体: AE-9×831x1=249
内能仅与自由度和温度有关,所以将“理想气体的内能只是温度的单值函数 作为理想气体的定义。 例:当温度为 0℃时,分别求氦、氢、氧。氨、氯和二氧化碳等气体各 1mol 的内能。温度升高 1K 时,内能各增加多说?(双原子以上分子均视为刚性分子) 解:按题意,对单原子气体的分子按三个平动自由度计算分子的平均动能, 对双原子或多原子气体按六个自由度计算分子平均动能。按上述公式,1mol 理 想气体的内能为 (t r 2s)kT 2 1 E mol = + + 可算出 0℃,即 273K 时,1mol 理想气体的内能分别为 单原子气体: 8.31 273 3.41 10 J 2 3 E 3 mol = = 双原子气体: 8.31 273 5.68 10 J 2 5 E 3 mol = = 三原子以上的气体: 8.31 273 6.81 10 J 2 6 E 3 mol = = 由 (t r 2s)kT 2 1 E mol = + + 可看到,当温度从 T 增加到 T + T 时,内能量增加 为 (t r 2s)k T 2 1 E mol = + + 所以温度每升高 1K 时,1mol 理想气体的内能增加 (t r 2s)k 2 1 + + , 单原子气体: 8.31 1 12.5J 2 3 E mol = = 双原子气体: 8.31 1 20.8J 2 5 E mol = = 三原子以上气体: 8.31 1 24.9J 2 6 E mol = =

§6一5麦克斯韦分子速率分布律 一、分布函数 1、它是一统计规律,对大量偶然事件,按某一性质(属性)研究其发生的 几率的规律 2、速率分布函数 设某一系统处于平衡态,分子总数为N,速率分布在某一区间v~v+△v内 的分子数△N。 则心N表示分布在V~V+△v区间内分子数占总分子数的比率。 显然: ①)对相同的区间间隔△,心与y有关 (2)给定v附近,N与v有关。 N 当Av→时,xAN -owa→0 即N=fWt,dy间隔,或fw=↓N 单位速率间隔 N dv 说明: 1、当v)哈定,V,~V,区间内分子数占总分子数的比率 袋-广vt,同隔 2、当V1=0,V2→0 f(v)dv=1,0~o间隔,归一化条件 二、麦克斯韦速率分布律 [1859年Maxwell,.Boltzmann等人从理论上(概率论、统计力学等)确定的, 以后被实验所证明] 在平衡状态下,当气体分子间相互作用可以忽略时,分布在任一速率区间 v~v+dv内的分子比率为
§6-5 麦克斯韦分子速率分布律 一、分布函数 1、它是一统计规律,对大量偶然事件,按某一性质(属性)研究其发生的 几率的规律 2、速率分布函数 设某一系统处于平衡态,分子总数为 N,速率分布在某一区间 v ~ v + v 内 的分子数 N。 则 表示分布在 N N v ~ v + v 区间内分子数占总分子数的比率。 显然: (1) 对相同的区间间隔 v, N N 与 v 有关; (2) 给定 v 附近, N N 与 v 有关。 当 v N N v 0 → 时,f(v) v( v 0) N N = → 即 f(v)dv N dN = ,dv 间隔,或 dv dN N 1 f(v) = ,单位速率间隔。 说明: 1、当 f(v)给定, v1 ~ v2 区间内分子数占总分子数的比率 f(v)dv N N 2 1 v v = , v1 ~ v2 间隔 2、当 v1 = 0,v2 → = 1 f(v)dv 1,0 ~ 间隔,归一化条件 二、麦克斯韦速率分布律 [1859 年 Maxwell,Boltzmann 等人从理论上(概率论、统计力学等)确定的, 以后被实验所证明] 在平衡状态下,当气体分子间相互作用可以忽略时,分布在任一速率区间 v ~ v + dv 内的分子比率为
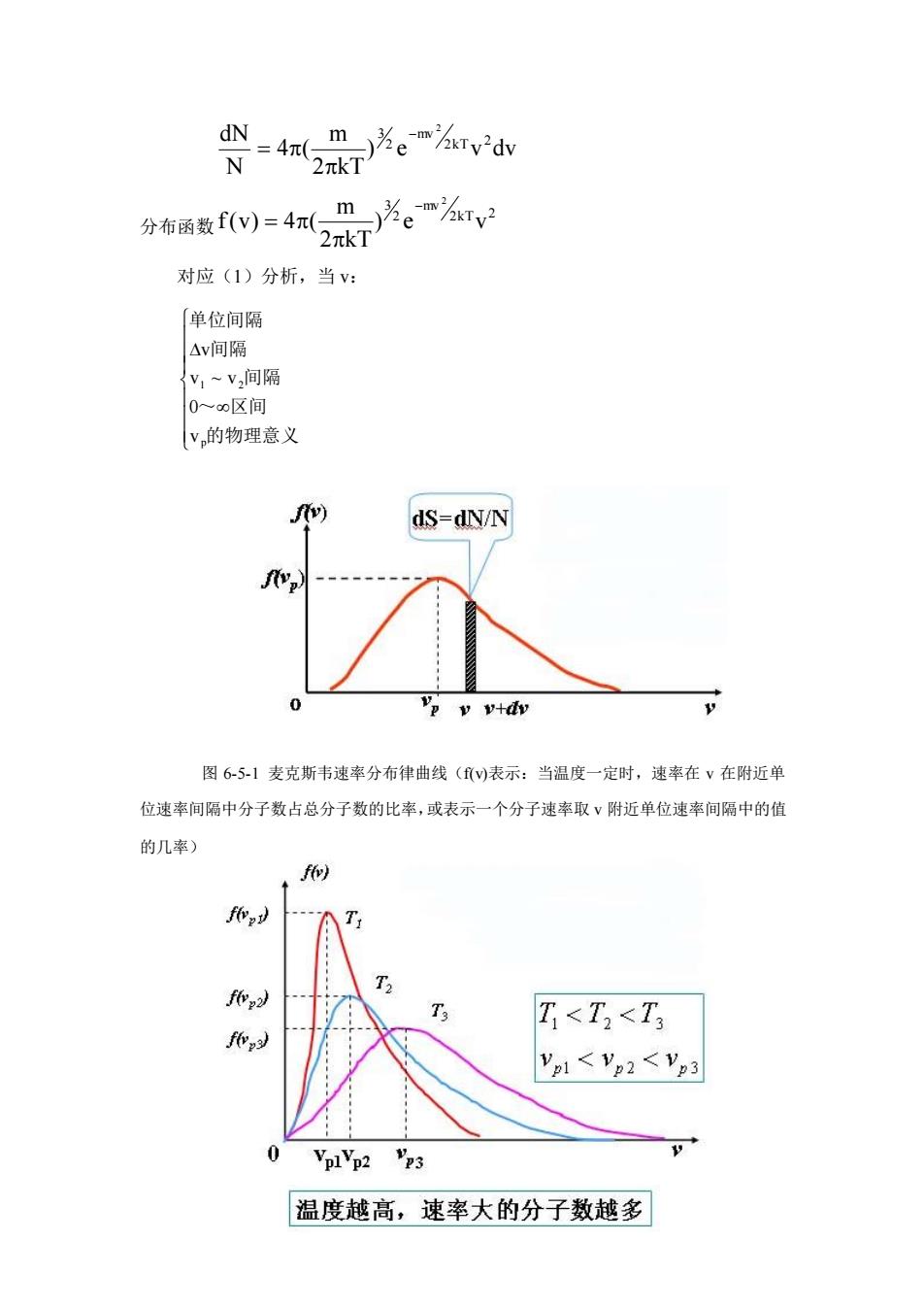
dN=4π_m-)为e'd N 2πkT1 责=27。% 对应(1)分析,当v: 「单位间隔 △v间隔 y1~v,间隔 0一区间 V的物理意义 dS=dN/N p vv+dy 图65-1麦克斯韦速率分布律曲线()表示:当温度一定时,速率在v在附近的 位速率间隔中分子数占总分子数的比率,或表示一个分子速率取V附近单位速率间隔中的值 的几率) f f T<T<T f Vpl V22<Vp3 VplVp2 温度越高,速率大的分子数越多
) e v dv 2 kT m 4 ( N dN 2kT 2 mv 2 3 2 − = 分布函数 2kT 2 mv 2 3 ) e v 2 kT m f(v) 4 ( 2 − = 对应(1)分析,当 v: 的物理意义 ~ 区间 间隔 间隔 单位间隔 p 1 2 v 0 v ~ v v 图 6-5-1 麦克斯韦速率分布律曲线(f(v)表示:当温度一定时,速率在 v 在附近单 位速率间隔中分子数占总分子数的比率,或表示一个分子速率取 v 附近单位速率间隔中的值 的几率)
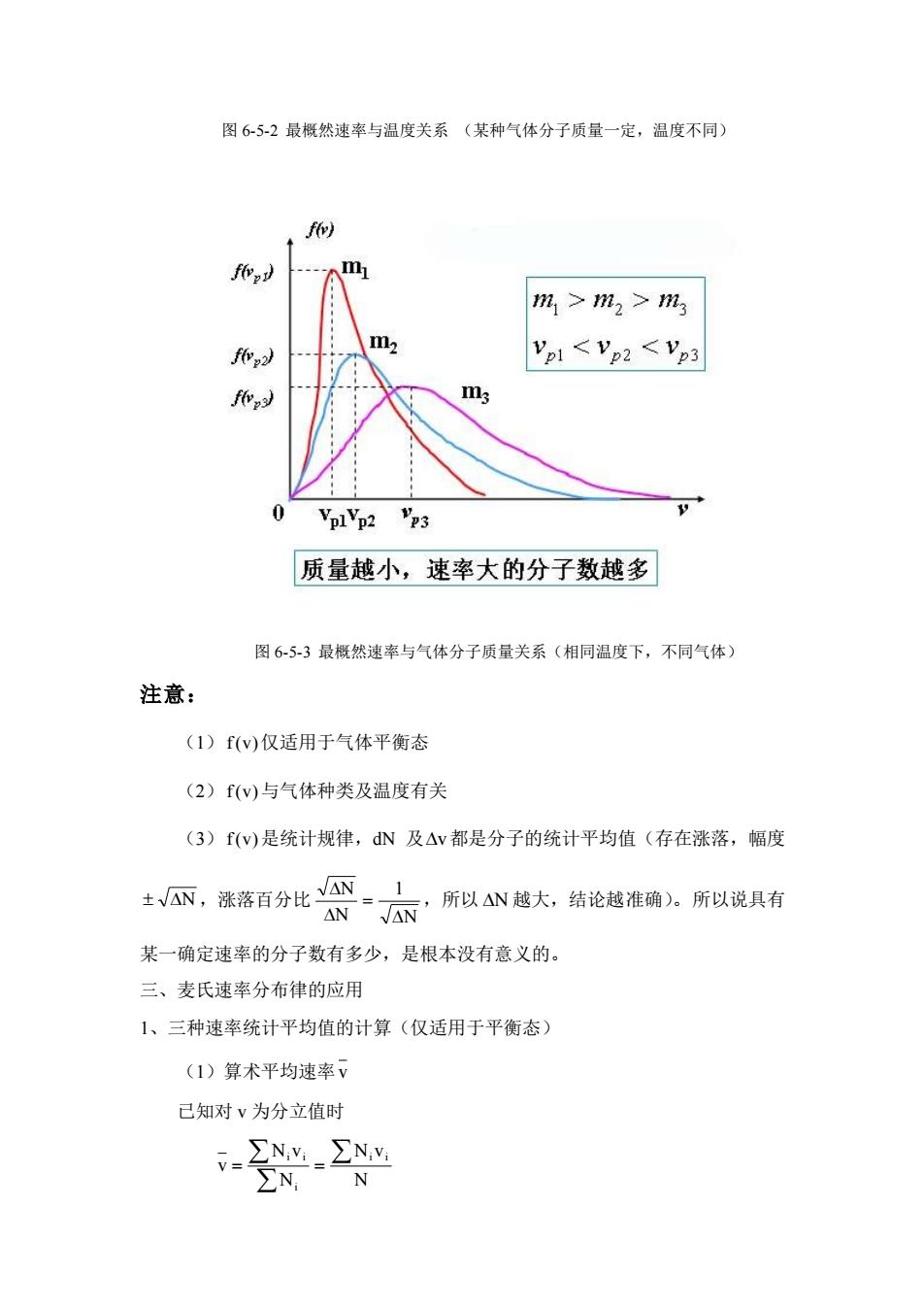
图65-2最概然速率与温度关系(某种气体分子质量一定,温度不同) 、f m m1>m2>m3 m fevy) VpI Vp2 <Vp3 fvs) VplVp2 23 质量越小,速率大的分子数越多 图65-3最概然速率与气体分子质量关系(相同温度下,不同气体) 注意: (1)f(v)仅适用于气体平衡态 (2)f(v)与气体种类及温度有关 (3)f(w)是统计规律,N及△v都是分子的统计平均值(存在涨落,幅度 ±。接落百分比深太·所以N越大,结论越准确。所以说具有 某一确定速率的分子数有多少,是根本没有意义的。 三、麦氏速率分布律的应用 1、三种速率统计平均值的计算(仅适用于平衡态) (1)算术平均速率V 已知对v为分立值时 V-ZNM.ENM ∑N N
图 6-5-2 最概然速率与温度关系 (某种气体分子质量一定,温度不同) 图 6-5-3 最概然速率与气体分子质量关系(相同温度下,不同气体) 注意: (1) f(v) 仅适用于气体平衡态 (2) f(v) 与气体种类及温度有关 (3) f(v) 是统计规律,dN 及 v 都是分子的统计平均值(存在涨落,幅度 N ,涨落百分比 N 1 N N = ,所以 N 越大,结论越准确)。所以说具有 某一确定速率的分子数有多少,是根本没有意义的。 三、麦氏速率分布律的应用 1、三种速率统计平均值的计算(仅适用于平衡态) (1)算术平均速率 v 已知对 v 为分立值时 N N v N N v v i i i i i = =