§13-4互感和自感 一互感 邻近线圈中电流的变 化引起另一个线圈产 生感应电动势的现象 称为互感现象 设Ψ21为1,的磁场在线圈2中的磁通链 数。由毕萨定律知 Ψ21
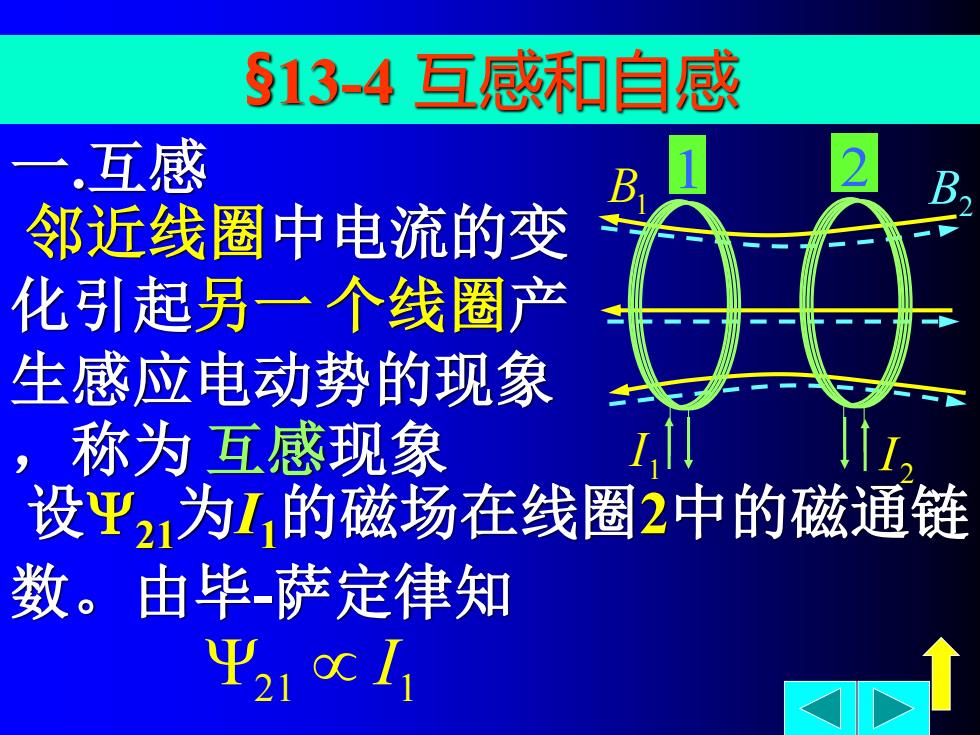
一 .互感 邻近线圈中电流的变 化引起另一 个线圈产 生感应电动势的现象 ,称为 互感现象 B1 B2 1 I 2 I 1 2 §13-4 互感和自感 设21为I1的磁场在线圈2中的磁通链 数。由毕-萨定律知 21 1 I

Y2 =M2I, M21: 线圈1对线圈2的互感系数 当I变化时,线圈2中的互感电动势 2= Y2-M2 dt 同理 €1= Y2=-M2 dt d M12: 线圈2对线圈1的互感系数
21 21 1 = M I M21:线圈1对线圈2的互感系数 当I1变化时,线圈2中的互感电动势 dt d 2 1 2 = − dt dI M 1 = − 2 1 同理 dt d 1 2 1 = − dt dI M 2 = − 1 2 M12:线圈2对线圈1的互感系数

可证M21=M2=M M:两回路间的互感系数,简称互感 单位:亨利H 说明 M与线圈的几何形状、匝数、相对 位置以及周围磁介质的磁导率有关 M的大小反映出两线圈间相互产生 感应电动势的能力
可证 M21 = M12= M M:两回路间的互感系数,简称互感 说明 :M与线圈的几何形状、匝数、相对 位置以及周围磁介质的磁导率有关 单位:亨利(H) M的大小反映出两线圈间相互产生 感应电动势的能力

[例⑧]半径为R的长直磁介质棒上,分 别绕有长为lN匝)和l,N,匝)的两个 螺线管.口由此特例证明M12=M21=M; 当螺线管1中的电流变化率为d亚/dt时 ,求螺线管2中的互感电动势 解:设螺线管1中通有电流I, ∴.B=un1
[例8]半径为R的长直磁介质棒上,分 别绕有长为l1 (N1匝)和l2 (N2匝)的两个 螺线管. 由此特例证明M12 =M21 =M; 当螺线管1中的电流变化率为dI1 /dt时 ,求螺线管2中的互感电动势 1 l 2 l 解: 设螺线管1中通有电流I1 1 1 1 B = n I 1 1 1 I l N =

通过螺线管2的磁通链数为 P21=NBS= LN N27R2I Z 又设螺线管2中通有电流I2,则 B2=Wn212=W
通过螺线管2的磁通链数为 21 = N2 B1 S 1 1 2 1 2 l N N R I = 1 2 1 2 1 I M = 1 2 1 2 l N N R = = n1 n2 V2 又设螺线管2中通有电流I2,则 2 2 2 B = n I 2 2 2 I l N =

因长直螺线管端口外磁场很快减小 为零,所以I,的磁场穿过螺线管1的 磁通链数为 Y2=☑BS=4mnlS=0nI23 12=mn2Y2 即有M2=M21=M LN N,TR dI E,=-M dt
因长直螺线管端口外磁场很快减小 为零,所以I2的磁场穿过螺线管1的 磁通链数为 n l B S 12 1 2 2 = 1 2 2 2 = n n I Sl 1 2 2 V2 = n n I 1 l 2 l 2 1 2 1 2 I M = = n1 n2 V2 即有 M12 = M21 = M dt dI i M 1 = − dt dI l N N R 1 1 2 1 2 = −

「例91两个同轴放置的圆形线圈C,和 C2,C,的面积S=4.0cm2,共有50匝; C,的半径R=20cm,共有100匝,求 两线圈的互感系数M; 当C,中的电 流以504的变化率减小时,求C中 的互感电动势。 解:·小线圈C的半径 r=√S/元≈1.1cm .r<<R
[例9]两个同轴放置的圆形线圈C1和 C2,C1的面积S=4.0cm2 ,共有50匝; C2的半径R=20cm,共有100匝,求 两线圈的互感系数M; 当C2中的电 流以50A/s的变化率减小时,求C1中 的互感电动势。 r C1 解: 小线圈 R C2 C1的半径 r = S / 1.1cm r R

设C,通以电流L,圆心处的磁感应强 度大小为 B= 4N212 2R 通过C线圈的全磁通 P12 N BS=HoNN212S 2R
设C2通以电流I2,圆心处的磁感应强 度大小为 R N I B 2 0 2 2 = r C1 R C2 通过C1线圈的全磁通 12 = N1 BS R N N I S 2 0 1 2 2 =
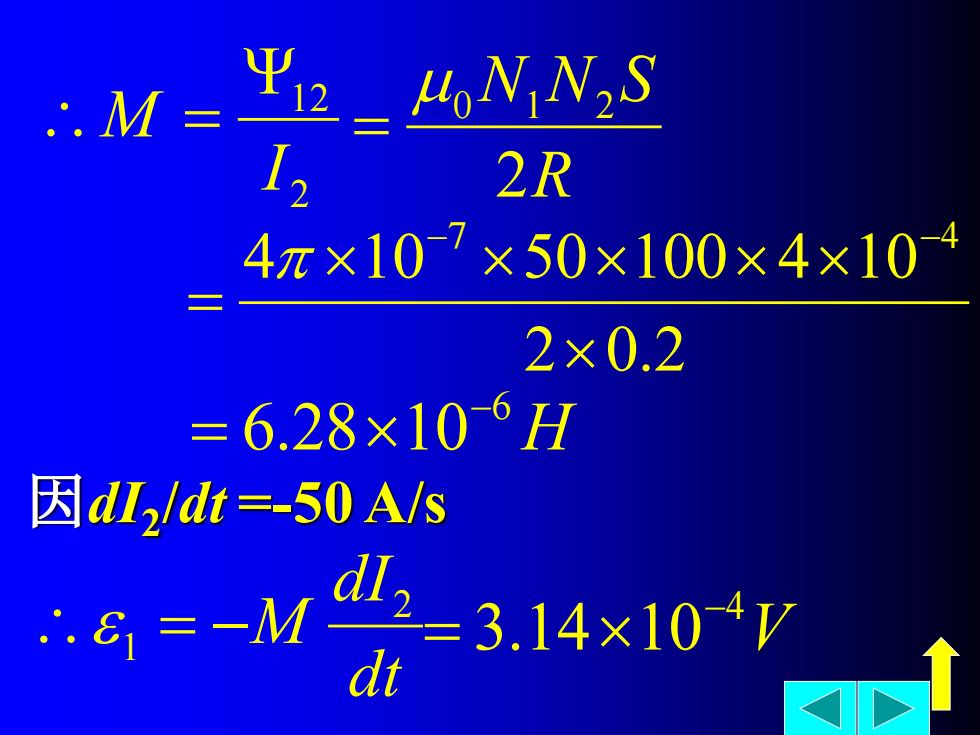
.M= HoN N2S 2R 4z×107×50×100×4×10 2×0.2 =6.28×106H 因dI/dt=-50A/s =-M-3.14x107 dt
2 0.2 4 10 50 100 4 10 7 4 = − − H 6 6.28 10− = 因dI2 /dt =-50 A/s dt dI M 2 1 = − V 4 3.14 10− = 2 12 I M = R N N S 2 0 1 2 =

二.自感 一个线圈自身电流的变化引起自身 线圈中产生感应电动势的现象,称 为自感现象 设一线圈中通有电流I,则穿过该回 路的磁通链数与成正比,即 Ψ=L7 L:自感系数,简称自感 单位:亨利H
二.自感 一个线圈自身电流的变化引起自身 线圈中产生感应电动势的现象,称 为自感现象 设一线圈中通有电流I,则穿过该回 路的磁通链数与I成正比,即 = LI L:自感系数,简称自感 单位:亨利(H)