第十章导体和介质中的静电场 §10-1静电场中的导体 一.导体与导体静电平衡的条件: ←- ←⊙ E=0 ←-⊙ ← 导体内部:E=E+E=0 导体表面:E≠0 归纳有二条: (1)导体内部任一点的场强都等于零。 (2)导体表面附近的场强和表面垂直。 由E=-VV=0三V=常数 U=∫Ed=0 →V-。=0 知:导体是等势体,导体表面是等势面。 二.导体电荷的分布: 由高斯定理:月Es=上∑9 】 由E,=0得:导体内部没有净电荷,电荷只能分布在表面。 有空腔时分成两种情况: 1.空腔内有其它带电体
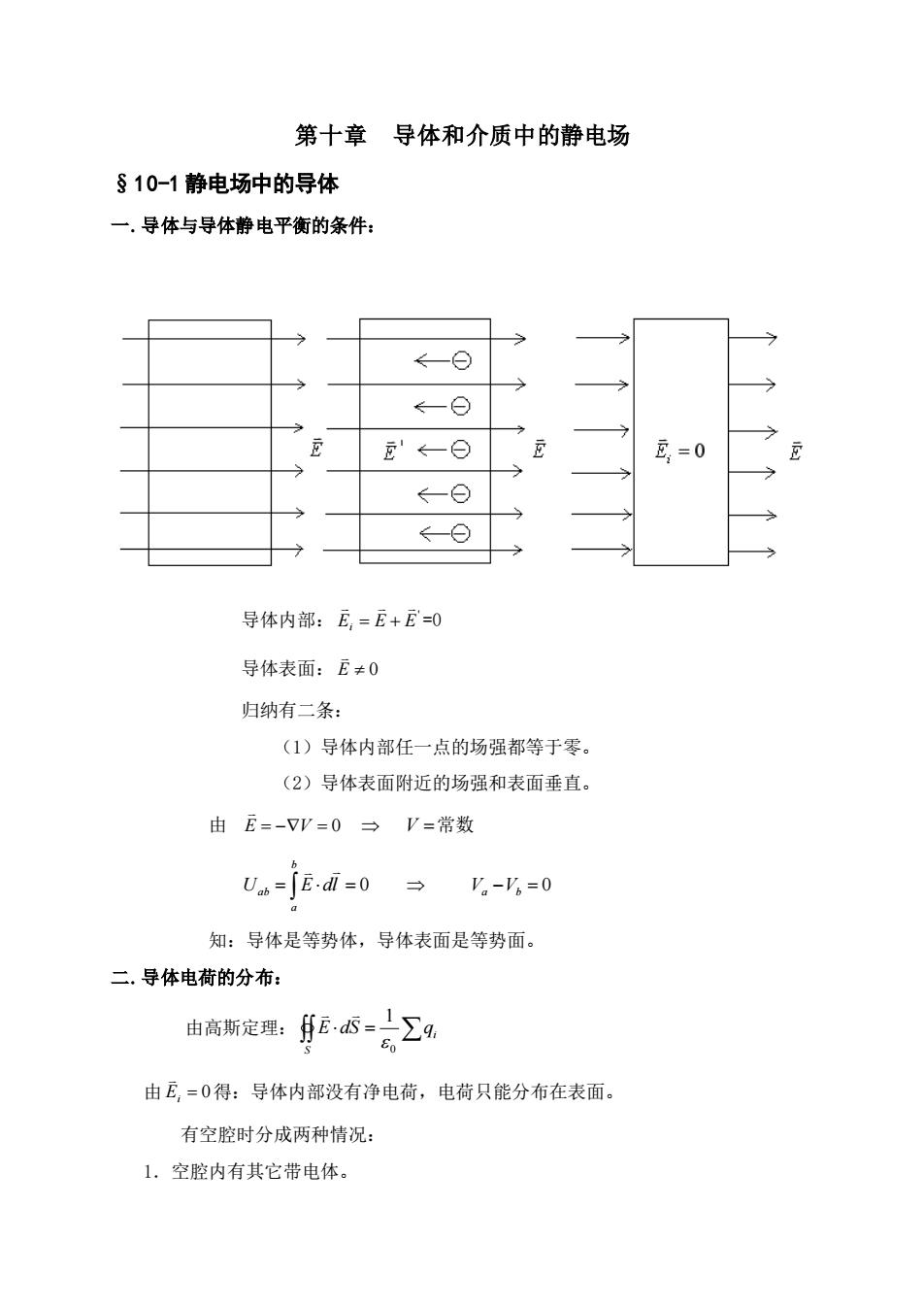
第十章 导体和介质中的静电场 §10-1 静电场中的导体 一.导体与导体静电平衡的条件: 导体内部: ' Ei E E = + =0 导体表面: E 0 归纳有二条: (1)导体内部任一点的场强都等于零。 (2)导体表面附近的场强和表面垂直。 由 E = −V = 0 V = 常数 = = b a ab U E dl 0 Va −Vb = 0 知:导体是等势体,导体表面是等势面。 二.导体电荷的分布: 由高斯定理: = i S E dS q 0 1 由 Ei = 0 得:导体内部没有净电荷,电荷只能分布在表面。 有空腔时分成两种情况: 1.空腔内有其它带电体

2.空腔内没有其它带电体。 导体处于静电平衡时有如下几个性质: ①导体是等势体,导体表面是等势面 ②导体内部没有静电荷,电荷只能分布在表面(包括内表面) ③紧靠导体表面外的各点场强方向与导体表面垂直。 若面密度为σ:则E= 5o 三.静电屏蔽: ①封闭导体(不论接地与否)内部电场不受壳外电荷的影响 ②接地封闭导体(或丝网)外部电场不受壳内电荷的影响 注意: ①无论导体壳内是否有电荷,壳外电荷的分布均不影响壳内场,但这并不 意味着壳外电荷不在壳内空间产生电场,而是壳外电荷与壳表面感应电荷 在壳内空间的合电场为零。 ②若壳不接地,则壳内电荷将影响壳外的场,但与壳内电荷的位置无关。 S10-2静电场中的电介质及其极化 一.极化的徽观机制 名日超 p=gl 分子电矩 1.无极分子的位移极化 HCH,He等 2.有极分子的取向极化 H0,HCL,NH,C0,S0,HS,甲醇,CH0L
2.空腔内没有其它带电体。 导体处于静电平衡时有如下几个性质: ① 导体是等势体,导体表面是等势面 ② 导体内部没有静电荷,电荷只能分布在表面(包括内表面) ③ 紧靠导体表面外的各点场强方向与导体表面垂直。 若面密度为 ;则 0 E = 三.静电屏蔽: ① 封闭导体(不论接地与否)内部电场不受壳外电荷的影响 ② 接地封闭导体(或丝网)外部电场不受壳内电荷的影响 注意: ① 无论导体壳内是否有电荷,壳外电荷的分布均不影响壳内场,但这并不 意味着壳外电荷不在壳内空间产生电场,而是壳外电荷与壳表面感应电荷 在壳内空间的合电场为零。 ② 若壳不接地,则壳内电荷将影响壳外的场,但与壳内电荷的位置无关。 §10-2 静电场中的电介质及其极化 一.极化的微观机制 1.无极分子的位移极化 H2 N2 CH4 He 等 2.有极分子的取向极化 H2O,HCL,NH3,CO,SO2,H2S,甲醇,CH3OH
室温下: 电介质的电阻率p三108-10欧·米 半导体p≈105~106 金属导体p≈10*~10 二.极化强度矢量P 1.△y中有∑P: 定义: 要 单位:库仑/米2 (单位体积内的电矩矢量和) 2。束缚电荷的分布与极化强度矢量的关系 设柱内极化是均匀的,△V很小,两底面出现的束缚(极化)电荷 面密度分别是+σ,-σ则整个斜柱体相当于一个偶极子,电矩为: ql-o'△S7;即:∑D=o△S7;△V=△S7cos8 按定义: 以②A
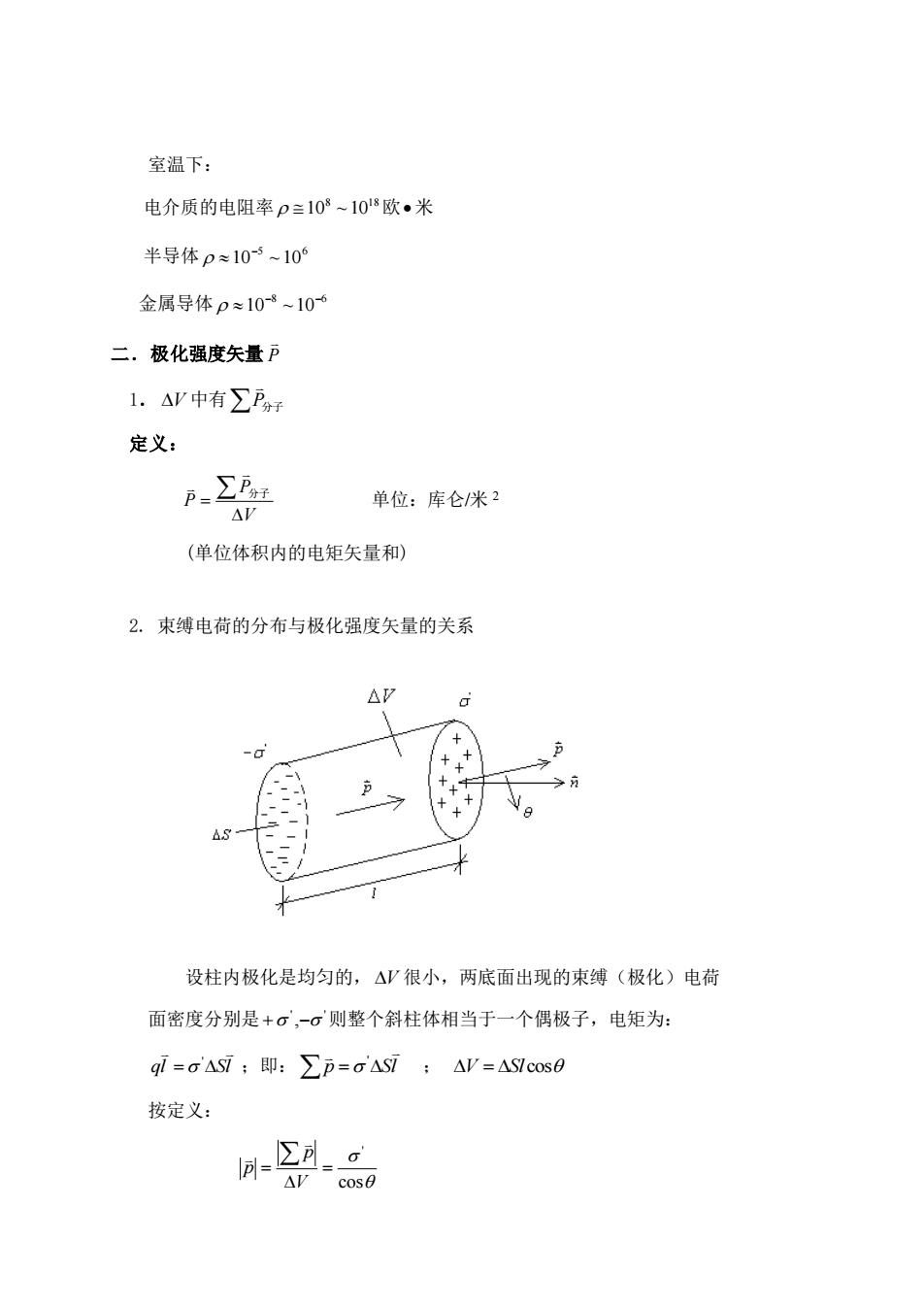
室温下: 电介质的电阻率 8 18 10 ~10 欧 • 米 半导体 5 6 10 ~10 − 金属导体 8 6 10 ~10 − − 二.极化强度矢量 P 1. V 中有 P分子 定义: V P P = 分子 单位:库仑/米 2 (单位体积内的电矩矢量和) 2. 束缚电荷的分布与极化强度矢量的关系 设柱内极化是均匀的, V 很小,两底面出现的束缚(极化)电荷 面密度分别是 ' ' + ,− 则整个斜柱体相当于一个偶极子,电矩为: ql Sl = ' ;即: p = Sl ' ; V = Sl cos 按定义: cos ' = = V p p

σ=|cos0=pn 即:=pn 故:σ等于D沿介质表面外法线方向的分量。 3.极化规律 如图:σ',-σ'产生的场E称为退极化场由场强叠加原理, 介质中的总场强E=E。+E,:实验表明,对大多数各个同性电介质, 有P=x,E其中x,叫做极化率,与E无关,只与介质的种类有关 三、电位移矢量D与有介质的高斯定理,介电常数 1.有介质时的高斯定理 到5西-,+9)为未知数 电介质 +σ' 为了消去q',以平行板电容器(两块无限大平行板)中充满均匀 电介质为帆。讨论如图造取圆柱商新面到形.香-,-0S) 己知p=o
= p = pn cos ' 即: p n = ' 故: ' 等于 p 沿介质表面外法线方向的分量。 3.极化规律 如图: ', ' − 产生的场 E 称为退极化场由场强叠加原理, 介质中的总场强 ' E E E = +0 0 ;实验表明,对大多数各个同性电介质, 有 P E = e 0 其中 e 叫做极化率,与 E 无关,只与介质的种类有关 三、电位移矢量 D 与有介质的髙斯定理,介电常数 1.有介质时的髙斯定理 = + S S E dS q q 内 ( ) 1 ' 0 0 为未知数 为了消去 q’,以平行板电容器(两块无限大平行板)中充满均匀 电介质为例,讨论如图选取圆柱髙斯面 = − S E dS ( S S ) 1 2 ' 0 1 0 已知 p= ', E ' E0 − ' + ' 电介质 ++++++++++++++ + ++++++++++++++ + — — — — — — — — — - — — — — — — — — — - + 0 - 0 - ' +

月P.5=月P.5=p心,=oS,6上的 fE-asps 定义:D=6E+P一般定义式,对一切介质成立。 月D5=g。为有介质时的高斯定理,9%是自由电荷。 2.DE,户三者关系: P=ZEE D=6E+P=60E+X5oE =8,1+X)E=E8,E=sE 6,称为相对介电常数 :称为绝对介电常数 §10-3电容电容器 一、孤立导体的电容 设孤立导体带电q,电势为U,则C=g/U:C只与导体的形状 大小、尺寸和环境有关,称为孤立导体的电容,单位是法拉(F)。 为了消除影响,采用静电屏蔽的办法,如图,DC对A无影响 同样可以定义电容C。一号.者B不接地,也可定义C可 仅仅与两导体的尺寸,形状和相对位置及环境有关。 二、电容器的计算 1.平行板电容器 设两板间的场强为E
= = = S S P dS P dS pS S2 ' 2 2 (S 上的) = − S S E dS S p dS 0 0 1 0 1 1 定义: D E P 0 = + 一般定义式,对一切介质成立。 = s D dS q0 为有介质时的髙斯定理, 0 q 是自由电荷。 2. D E P , , 三者关系: 0 0 0 0 0 0 r (1 ) e e e P E D E P E E E E E = = + = + = = + = r 称为相对介电常数 称为绝对介电常数 §10-3 电容 电容器 一、孤立导体的电容 设孤立导体带电 q,电势为 U ,则 C=q/ U ;C 只与导体的形状 大小、尺寸和环境有关,称为孤立导体的电容,单位是法拉( F )。 为了消除影响,采用静电屏蔽的办法,如图,DC对 A 无影响, 同样可以定义电容 A AB A q C U = 。若 B 不接地,也可定义 A AB A B q C U U = − 仅仅与两导体的尺寸,形状和相对位置及环境有关。 二、电容器的计算 1. 平行板电容器 设两板间的场强为 E

由f0西=,E=名 u,-,=h-gg=0 c=u,号 若两板间是真空,C=.二。」 dc-s 2.圆柱形电容器 设内外极板分别带电十q,一q,9。=汕,为线电荷密度 E=-亚0-了w dr 27R 3.球形电容器 E=名由高斯定理求得。 0=-bd=4 q _4πER,RB AIE R Ra 计算电容的步骤: (1)设电容器两极上分别带电荷±g,计算两级间的场强分布从而算出U (②所设的U。必然与9成正比,利用电容的定义C一乙
由 = s D dS q0 , E = q s d U A −UB = Ed = , = d s U U q C A B = − = 若两板间是真空, ' 0 1 ' , r s C C d C = = 2. 圆柱形电容器 设内外极板分别带电+q,-q, 0 q l = , 为线电荷密度 E 2 r = , , 2 B B A A U R U R dU dr E dU Edr dU dr r = − = − = − ln 2 B A B A R U U R − = 2 ln ln 2 A B B B A A q l l C U U R R R R = = = − 3. 球形电容器 2 4 q E r = 由髙斯定理求得。 2 4 q dU Edr dr r = − = − 1 1 ( ) 4 A B A B q U U R R − = − , 4 1 1 ( ) 4 A B A B B A A B q q R R C U U R R q R R = = = − − − 计算电容的步骤: (1)设电容器两极上分别带电荷 q ,计算两级间的场强分布从而算出 UAB (2)所设的 UAB 必然与 q 成正比,利用电容的定义 AB q C U =

§10-4电场的能量 一、电荷系统的能量 设ql,q2原来相距无穷远,先将ql迁移到a点固定下来, 再将q2迁移到b点固定下来。 外力做功4=4心-U,-品儿=0 A=9q0,=40 ,194颠倒q,9的顺序,同样得到结果。 根据功能原理, W=A=E r 1942 将式子改写为 w-+5-,+w 同理可以讨论3个,4个电荷系统以其推广 对n个点电荷组成的带电系统 W=之9心,这里计算的由几个点电荷组间的内能, 不包括每个点电荷的自能。 U,表示除第i个点电荷之外所有其他-1个点电荷在第i个点电荷 处所产生的电势(对有介质时,上式也成立,1是有介质时的电势) 二、连续分布情形的静电能(电荷分布已形成) 利用一9(山)以体电为例,分制带电体成许多 体积元△业,设电荷体密度为P,=)∑P,A吧
§10-4 电场的能量 一、电荷系统的能量 设 q1,q2 原来相距无穷远,先将 q1 迁移到 a 点固定下来, 再将 q2 迁移到 b 点固定下来。 外力做功 1 2 2 2 0 ( ), , 0 4 q A q U U U U r = − = = 1 2 2 2 0 1 4 q q A q U r = = 颠倒 1 2 q ,q 的顺序,同样得到结果。 根据功能原理, 1 2 0 1 4 q q W A r = = 将式子改写为 2 1 1 2 1 1 2 2 0 0 1 1 1 1 2 4 2 4 2 2 q q W q q q U q U r r = + = + 同理可以讨论 3 个,4 个电荷系统以其推广 对 n 个点电荷组成的带电系统 1 1 2 n i i i W qU = = ,这里计算的由几个点电荷组间的内能, 不包括每个点电荷的自能。 Ui 表示除第 i 个点电荷之外所有其他 n-1 个点电荷在第 i 个点电荷 处所产生的电势(对有介质时,上式也成立,Ui 是有介质时的电势) 二、 连续分布情形的静电能(电荷分布已形成) 利用 1 1 2 n i i i W qU = = ( 1 2 Q Udq )以体电荷为例,分割带电体成许多 体积元 Vi ,设电荷体密度为 e , 1 2 e e i i i W VU =

当Ay→0R=)J∬pU 注意:写成积分表示带电体已被无限分割,因此上式求的已经是 包括自能在内的静电能W,其中,U是dv处的电势,可以是变的 化=ak,面密度 同理: 用=打2Udl,线密度 电场的能量: 将以上结果应用到平行板电容器上, U。=Ed,C=ei w-cwi-rd-tw-eE E是均匀的.W也是均匀的 无介质时纯粹是电场的能量,有介质时还包含介质的极化能。 电场能量的体密度 -"-ce'-i 推广:普遍适用的公式 电场总能量:W=∬odW=)DEd 能量定域在电场中的,V是整个电场存在的空间
当 ' 1 0, 2 i e e v → = V W Udv 注意:写成积分表示带电体已被无限分割,因此上式求的已经是 包括自能在内的静电能 We 其中, U 是 dv 处的电势,可以是变的 同理 : ' L' 1 , 2 1 Udl, 2 e s e W Uds W = = 面密度 线密度 电场的能量: 将以上结果应用到平行板电容器上, AB 2 2 2 2 2 s U Ed = d 1 1 s 1 1 E d E E 2 2 d 2 2 W CU sd V AB = = = = = ,C E是均匀的W也是均匀的 无介质时纯粹是电场的能量,有介质时还包含介质的极化能。 电场能量的体密度 推广:普遍适用的公式 电场总能量: 1 2 v v W dV DEdV = = 能量定域在电场中的,V 是整个电场存在的空间 E DE V W we 2 1 2 1 2 = = =