
第2章牛顿运动定律 上图为安装在纽约联合国总部的傅科摆
第2章 牛顿运动定律 上图为安装在纽约联合国总部的傅科摆

§2.1牛顿运动三定律 一.牛顿第一定律 任何质点都保持静止或匀速直线运动状态,直到其它物体 作用的力迫使它改变这种状态为止。 第一定律引进了二个重要概念 。惯性一 质点不受力时保持静止或匀速直线运动状 态的的性质,其大小用质量量度。 力 使质点改变运动状态的原因 质点处于静止或匀速直线运动状态时: ∑=0 (静力学基本方程)
§2.1 牛顿运动三定律 任何质点都保持静止或匀速直线运动状态,直到其它物体 作用的力迫使它改变这种状态为止。 第一定律引进了二个重要概念 惯性 —— 质点不受力时保持静止或匀速直线运动状 态的的性质,其大小用质量量度。 力 —— 使质点改变运动状态的原因 = 0 Fi 质点处于静止或匀速直线运动状态时: ( 静力学基本方程 ) 一. 牛顿第一定律 • •

二,牛顿第二定律 某时刻质点动量对时间的变化率正比与该时刻作用在质点上 所有力的合力。 ∑Fx (mi) ∑F=k(mD dt 取适当的单位,使k=1,则有 d(mi)dm )+m di 当物体的质量不随时间变化时 Σ=m =ma ·直角坐标系下为 "x ∑F=m y ∑Fn=m ∑F=m
二. 牛顿第二定律 某时刻质点动量对时间的变化率正比与该时刻作用在质点上 所有力的合力。 t m Fi d d( v) 取适当的单位,使k =1 ,则有 t m t m t m Fi d d d d d d( ) v v v = = + ma t Fi m = = d dv 当物体的质量不随时间变化时 t m F k i d d( v) = 直角坐标系下为 = d d 2 2 t x Fix m • = 2 2 d d t y Fiy m = 2 2 d d t z Fiz m

·自然坐标下 ∑Fn=ma 三m ∑F=ma,=m 讨论 (1)第二定律只适用于质点的运动情况 2)以下两种情况下,质量不能当常量 。物体在运动中质量有所增减,如火箭、雨滴问题。 。高速(v>10m/s)运动中,质量与运动速度相关,如 相对论效应问题
讨论 (1) 第二定律只适用于质点的运动情况 2 2 ) d d ( 1 t s Fn man m m = = = v 自然坐标下 2 2 d d d d t s m t F ma m τ τ = = = v 物体在运动中质量有所增减,如火箭、雨滴问题。 高速(v > 106 m/s ) 运动中,质量与运动速度相关,如 相对论效应问题。 (2) 以下两种情况下,质量不能当常量 • • •

三.牛顿第三定律 当物体A以力方作用于物体B时,物体B也同时以力F 作用于物体A上,户和F总是大小相等,方向相反, 且在同一直线上。 F=-F 第三定律揭示了力的两个性质 ·成对性一 物体之间的作用是相互的。 。同时性 相互作用之间是相互依存,同生同灭。 讨论 第三定律是关于力的定律,它适用于接触力。对于非接触的 两个物体间的相互作用力,由于其相互作用以有限速度传播, 存在延迟效应
F F' = − 三. 牛顿第三定律 第三定律揭示了力的两个性质 成对性 —— 物体之间的作用是相互的。 同时性 —— 相互作用之间是相互依存,同生同灭。 当物体 A 以力 F 作用于物体B 时,物体 B 也同时以力 F 作用于物体A 上, F 和 F 总是大小相等,方向相反, 且在同一直线上。 • • 讨论 第三定律是关于力的定律,它适用于接触力。对于非接触的 两个物体间的相互作用力,由于其相互作用以有限速度传播, 存在延迟效应

§2.2力学中常见的几种力 一.万有引力 质量为m、2, 相距为r的 两质点间的万有引力大小为 F= m G=6.67×10lm3.kg 用失量表示为1=-G刀 说明 (1)依据万有引力定律定义的质量叫明引力质量,常见的用天 平称量物体的质量,实际上就是测明引力质量;依据牛顿 第二定律定义的质量叫惯性质量。实验表明:对同一物 体来说,两种质量总是相等
§2.2 力学中常见的几种力 一. 万有引力 m1 m2 F21 0 F12 r 质量为 r m1、m2 ,相距为r 的 两质点间的万有引力大小为 2 1 2 r m m F = G 11 3 1 2 6.67 10 m kg s − − − G = 用矢量表示为 0 2 1 2 21 r r m m F = −G 说明 (1) 依据万有引力定律定义的质量叫引力质量,常见的用天 平称量物体的质量,实际上就是测引力质量;依据牛顿 第二定律定义的质量叫惯性质量。实验表明:对同一物 体来说,两种质量总是相等

(2)万有引力定律只直接适用于两质点间的相互作用 例如图所示,一质点旁边放一长度为L、质量为M的杆, 杆离质点近端距离为!。 求该系统的万有引力大小。 M 解 F=GmM/12? dM=Adx x 质点与质量无间的万有引力大小为 df=GmdM 杆与质点间的万有引力大小为 mM 1+ 当1>L时60+0 mM →G☑
如图所示,一质点m 旁边放一长度为L 、质量为M 的杆, 杆离质点近端距离为l 。 m M L 解 l 例 求 该系统的万有引力大小。 2 2 d d d Lx mM x G x m M f = G = dM = dx x o dx ? 2 F = GmM l x + + + = = = l L l l L l l L l x x L mM x G Lx mM f f G 2 2 d d d l(l L) mM G + = 当 l >>L 时 l(l L) mM G + 2 l mM → G (2) 万有引力定律只直接适用于两质点间的相互作用 杆与质点间的万有引力大小为 质点与质量元间的万有引力大小为

(3)重力是地球对其表面附近物体万有引力的分力 设地球半经为R,质量为M,物体质量为m,考虑地 球自转后物体重力为 为物体所处的地理纬度角 P=( Mm 1-0.0035cos2p) 二,弹性力 无形变,无弹性力 。当两宏观物体有接触且发生微小形变 时,形变的物体对与它接触的物体会 产生力的作用,这种力叫弹性力。 。在形变不超过一定限度内,弹簧的弹 性力遵从胡克定律 f=-x司 绳子在受到拉伸时,其内部也同样出现弹性张力
(1 0.0035cos ) 2 2 = − R Mm P G (3) 重力是地球对其表面附近物体万有引力的分力 为物体所处的地理纬度角 设地球半经为R ,质量为M ,物体质量为m ,考虑地 球自转后物体重力为 二. 弹性力 当两宏观物体有接触且发生微小形变 时,形变的物体对与它接触的物体会 产生力的作用,这种力叫弹性力。 • 在形变不超过一定限度内,弹簧的弹 性力 遵从胡克定律 • f kx i = − • 绳子在受到拉伸时,其内部也同样出现弹性张力。 N N' P 无形变,无弹性力
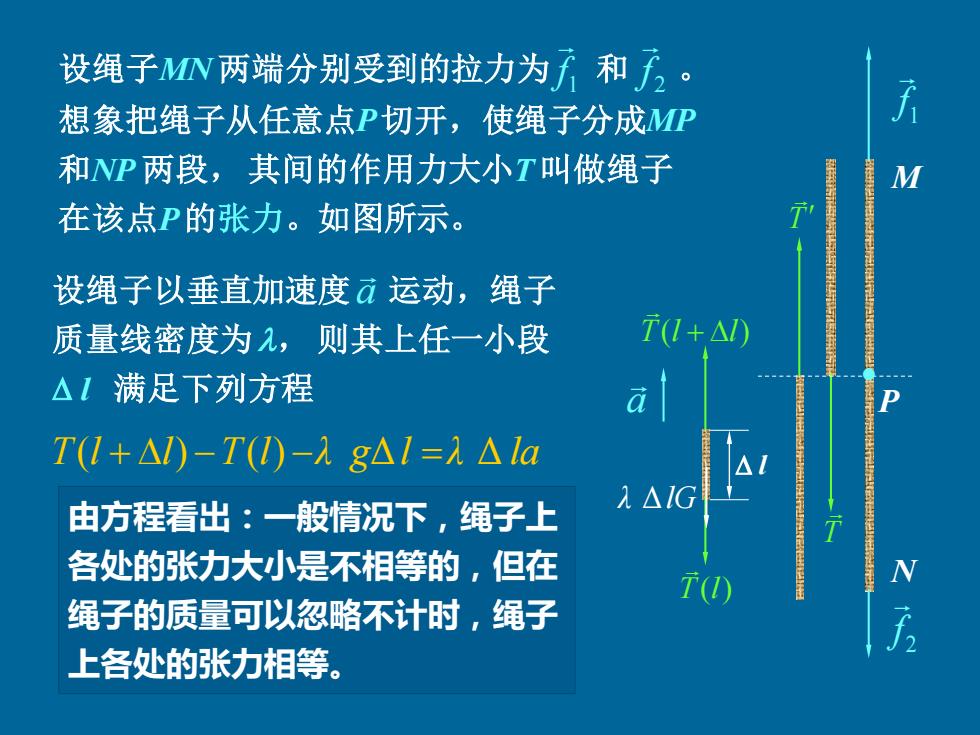
设绳子MN两端分别受到的拉力为f和f)。 想象把绳子从任意点P切开,使绳子分成MP 和NP两段,其间的作用力大小T叫做绳子 M 在该点P的张力。如图所示。 设绳子以垂直加速度ā运动,绳子 质量线密度为入,则其上任一小段 TI+△V0 △1满足下列方程 T(l+△)-T(I)-λg△I=△l1a 2△1G 由方程看出:一般情况下,绳子上 各处的张力大小是不相等的,但在 绳子的质量可以忽略不计时,绳子 上各处的张力相等
设绳子MN 两端分别受到的拉力为 和 。 T(l) T(l + l) M N P T T 1 f 2 f 想象把绳子从任意点P 切开,使绳子分成MP 和NP 两段, 其间的作用力大小T 叫做绳子 在该点P的张力。如图所示。 1 f 2 f 设绳子以垂直加速度 运动,绳子 质量线密度为, 则其上任一小段 l 满足下列方程 a T(l + l) −T(l) −λ gΔl =λ Δ la λ ΔlG l 由方程看出:一般情况下,绳子上 各处的张力大小是不相等的,但在 绳子的质量可以忽略不计时,绳子 上各处的张力相等。 • a

四.摩擦力 1.静摩擦力 当两相互接触的物体彼此之间保持相对静止,且沿接触面有 相对运动趋势时,在接触面之间会产生一对阻止上述运动趋 势的力,称为静摩擦力。 说明 静摩擦力的大小随引起相对运动趋势的外力而变化。最大 静摩擦力为fmx=,N(,为最大静摩擦系数,N为正压力) 2.滑动摩擦力 两物体相互接触,并有相对滑动时,在两物体接触处出现 的相互作用的摩擦力,称为滑动摩擦力。 ∫=uN(μ为滑动摩擦系数)
四. 摩擦力 当两相互接触的物体彼此之间保持相对静止,且沿接触面有 相对运动趋势时,在接触面之间会产生一对阻止上述运动趋 势的力,称为静摩擦力。 1. 静摩擦力 说明 静摩擦力的大小随引起相对运动趋势的外力而变化。最大 静摩擦力为 fmax=µ0 N 2. 滑动摩擦力 两物体相互接触,并有相对滑动时,在两物体接触处出现 的相互作用的摩擦力,称为滑动摩擦力。 f =μ N ( µ0 为最大静摩擦系数,N 为正压力) ( µ 为滑动摩擦系数)