
第8章 静电场 图为1930年E.O.劳伦斯制成的世界上第一台回旋加速器
第8章 静电场 图为1930年E.O.劳伦斯制成的世界上第一台回旋加速器

88.1电荷 库仑定律 一.电荷 1.正负性 2.量子性 O=ne e=(1.6021892±0.0000046)×10-19G 盖尔一曼提出夸克模型:± 3 3.守恒性 在一个孤立系统中总电荷量是不变的。即在任何时刻系统 中的正电荷与负电荷的代数和保持不变,这称为电荷守恒 定律。 4.相对论不变性 电荷的电量与它的运动状态无关
§8.1 电荷 库仑定律 一.电荷 1. 正负性 2. 量子性 e (1.602 189 2 0.000 004 6) 10 C −19 Q = ne = 盖尔—曼提出夸克模型 : e 3 1 e 3 2 3. 守恒性 在一个孤立系统中总电荷量是不变的。即在任何时刻系统 中的正电荷与负电荷的代数和保持不变,这称为电荷守恒 定律。 4. 相对论不变性 电荷的电量与它的运动状态无关

二,库仑定律 1.点电荷 当带电体的大小、形状与带电体间的距离相比可以忽略时, 就可把带电体视为一个带电的几何点。(一种理想模型) 2.库仑定律 处在静止状态的两个点电荷,在真空(空气)中的相互作用 力的大小,与每个点电荷的电量成正比,与两个点电荷间距 离的平方成反比,作用力的方向沿着两个点电荷的连线。 电荷q,对2的作用力F2 5,=k99 91 92
二. 库仑定律 1. 点电荷 (一种理想模型) 当带电体的大小、形状 与带电体间的距离相比可以忽略时, 就可把带电体视为一个带电的几何点。 2. 库仑定律 处在静止状态的两个点电荷,在真空(空气)中的相互作用 力的大小,与每个点电荷的电量成正比,与两个点电荷间距 离的平方成反比,作用力的方向沿着两个点电荷的连线。 q1 2 q r 21 r 2 1 2 21 r q q F = k 0 2 21 1 2 21 r r q q F k = 电荷q1 对q2 的作用力F21 F21

电荷2对q的作用力F12 941 42 F2=k华8 F2 2 k= 6,一真空中的电容率(介电常数) 4π80 8=8.85418782×1012F/m 992 4元80 讨论: ()库仑定律适用于真空中的点电荷; (2)库仑力满足牛顿第三定律: 3)一般F电>F万
电荷q2对q1的作用力F12 0 2 12 1 2 12 r r q q F k = q1 2 q r 12 r F12 4 0 1 k = 0 真空中的电容率(介电常数) 8.854 187 82 10 F/m 12 0 − = 0 2 1 2 4 0 1 r r q q F = 讨论: (1) 库仑定律适用于真空中的点电荷; (2) 库仑力满足牛顿第三定律; (3) 一般 F电 F万
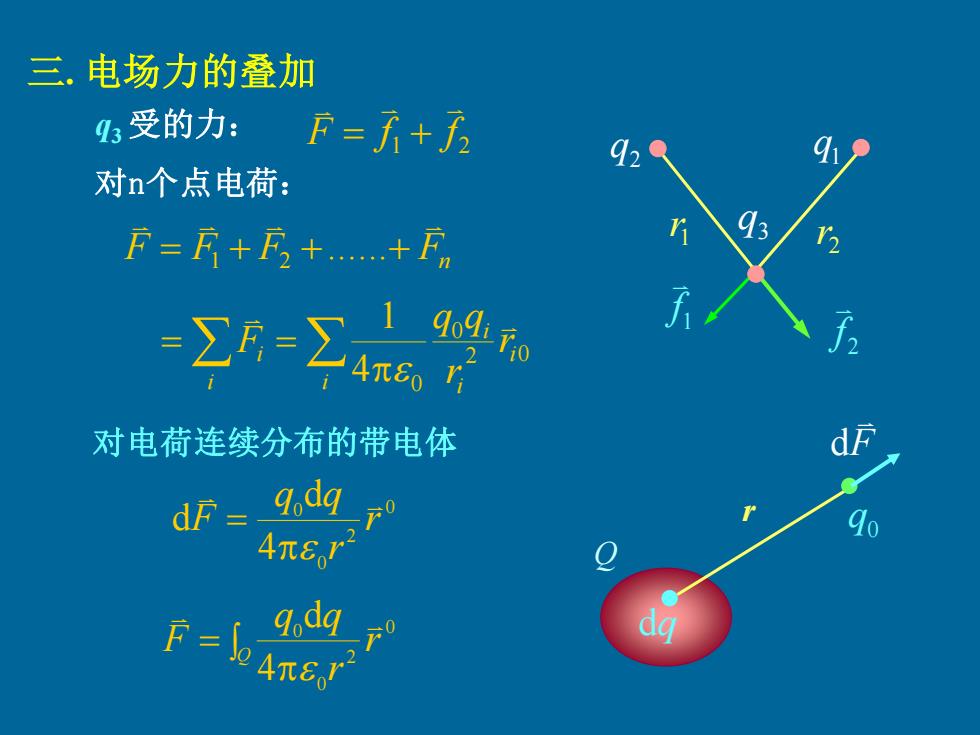
三.电场力的叠加 ⅓受的力: F=才+方 对n个点电荷: F=万+F++F 25-2462 q470 对电荷连续分布的带电体 dF= qdq 4πer2 F=0
三. 电场力的叠加 1 2 F f f = + 1 r 2 r 1 q q3 2 q 1 f 2 f q3 受的力: F F F Fn = 1 + 2 +.+ 2 0 0 4 0 1 i i i i i i r r q q F = = 对n个点电荷: 对电荷连续分布的带电体 0 2 0 0 4 d d r r q q F = = Q r r q q F 0 2 0 0 4 d Q r dq q0 F d

例已知两杆电荷线密度为入,长度为L,相距L 求两带电直杆间的电场力。 解 dq Adx dq dq' dq'Adx' o x 2L x 3L Adx Adx' dF 4πE(x'-x) Pdx 4 4π6(x'-x 4π80 3
已知两杆电荷线密度为,长度为L,相距L 解 dq x x dq = dx dq = dx dq 2 0 4 ( ) d d d x x x x F − = − = L L L x x x F x 3 2 0 2 0 2 4 ( ) d d 例 求 两带电直杆间的电场力。 3 4 ln 4 0 2 = O L 2L 3L x

88.2静电场 电场强度卫 一.静电场 ·早期:电磁理论是超距作用理论 ·后来:法拉第提出场的概念 ·电场的特点 (1)对位于其中的带电体有力的作用 (2)带电体在电场中运动,电场力要作功 二.电场强度 场源电荷一产生电场的电荷 带电量足够小 检验电荷 点电荷 在电场中任一位置处: 91 42
§8.2 静电场 电场强度E 一. 静电场 后来: 法拉第提出场的概念 早期:电磁理论是超距作用理论 电场的特点 (1) 对位于其中的带电体有力的作用 (2) 带电体在电场中运动,电场力要作功 二. 电场强度 检验电荷 带电量足够小 点电荷 场源电荷 产生电场的电荷 = = F1 F2 2 q1 q E 在电场中任一位置处:
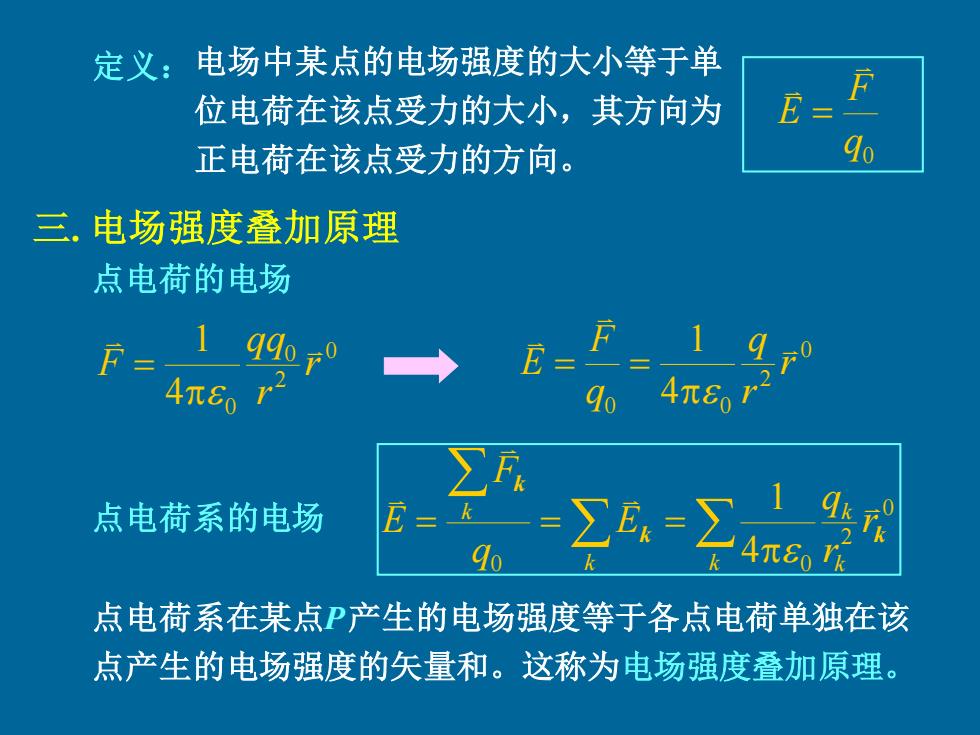
定义:电场中某点的电场强度的大小等于单 位电荷在该点受力的大小,其方向为 E= F 正电荷在该点受力的方向。 9o 三,电场强度叠加原理 点电荷的电场 1 q9o-o E=" 4π607 4πr2 点电荷系的电场 E= ∑E之4r67 点电荷系在某点P产生的电场强度等于各点电荷单独在该 点产生的电场强度的矢量和。这称为电场强度叠加原理
电场中某点的电场强度的大小等于单 位电荷在该点受力的大小,其方向为 正电荷在该点受力的方向。 三. 电场强度叠加原理 点电荷的电场 0 2 0 4 0 1 r r qq F = 0 2 0 0 4 1 r r q q F E = = = = = k k k k k r r q E q F E 0 2 0 4 0 1 k k k 定义: 点电荷系的电场 点电荷系在某点P产生的电场强度等于各点电荷单独在该 点产生的电场强度的矢量和。这称为电场强度叠加原理。 0 q F E =

连续分布带电体 1 dE dE 4πET E= dq Adl (线分布) 入:线密度 odS (面分布) O:面密度 odV (体分布) P:体密度
连续分布带电体 0 2 0 d 4 1 d r r q E = = 0 2 4 0 d r r q E dq = : 线密度 : 面密度 : 体密度 dq r E d P dl (线分布) dS (面分布) dV (体分布)
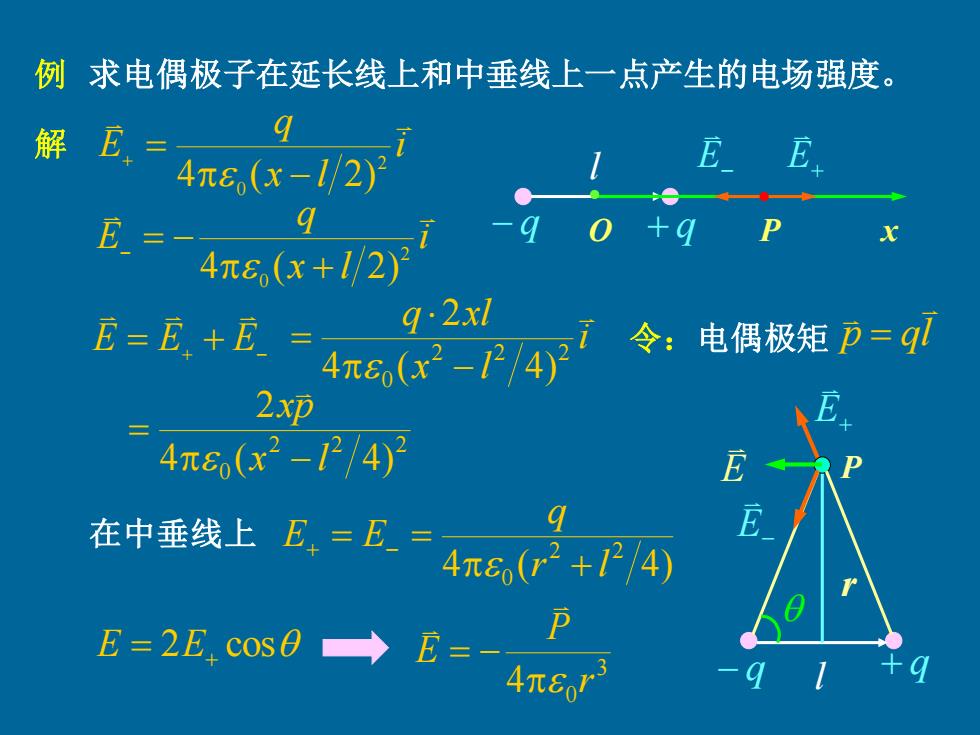
例求电偶极子在延长线上和中垂线上一点产生的电场强度。 解E= q 4π6(x-1/2) E B.=- +q π6,(x+1/2) E=E.+E q:2xl 4πe(cx2-P/4令 电偶极矩p=q 2xp 4元6(x2-1P/4)月 在中垂线上E,=E=4πE(G2+4) E=2Ecos0→ 4π6T
求电偶极子在延长线上和中垂线上一点产生的电场强度。 − q + q l 解 E− E+ i x l q E 2 0 4 ( − 2) + = 例 i O P x x l q E 2 0 4 ( + 2) − = − E = E+ + E− i x l q xl 2 2 2 0 4 ( 4) 2 − = p ql = 2 2 2 0 4 ( 4) 2 x l xp − = 令:电偶极矩 − q + q l P r E− E+ E 4 ( 4) 2 2 0 r l q E E + + = − = 在中垂线上 E = 2E+ cos 3 0 4 r P E = −