第6章测体动力学 猫习惯于在阳台上睡觉,因而从阳台上掉下来的事情时有发生。长期 的观察表明猫从高层楼房的阳台掉到楼外的人行道上时,受伤的程度 将随高度的增加而减少,为什么会这样呢?
第6章 刚体动力学 猫习惯于在阳台上睡觉,因而从阳台上掉下来的事情时有发生。长期 的观察表明猫从高层楼房的阳台掉到楼外的人行道上时,受伤的程度 将随高度的增加而减少,为什么会这样呢?
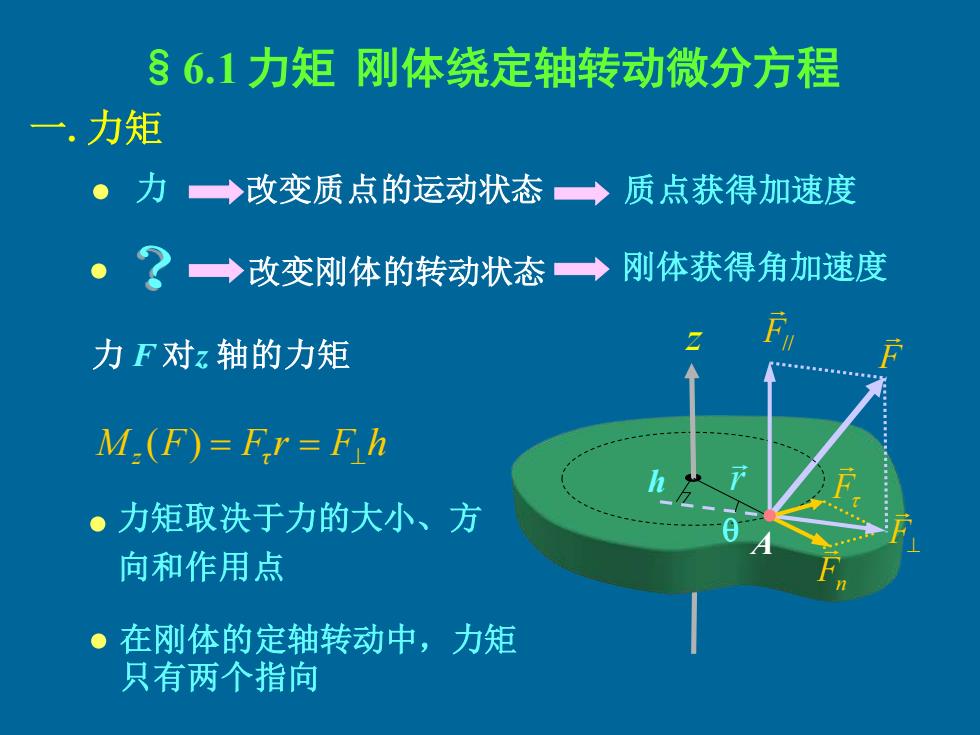
§6.1力矩刚体绕定轴转动微分方程 一力矩 ·力→改变质点的运动状态◆质点获得加速度 。?一→改变刚体的转动状态→刚体获得角加速度 力F对z轴的力矩 M.(F)=Fr=Fh 。力矩取决于力的大小、方 向和作用点 ●在刚体的定轴转动中,力矩 只有两个指向
§6.1 力矩 刚体绕定轴转动微分方程 一. 力矩 力 改变刚体的转动状态 刚体获得角加速度 力 F 对z 轴的力矩 Mz (F) = Fτ r = F⊥h 力矩取决于力的大小、方 向和作用点 在刚体的定轴转动中,力矩 只有两个指向 • • • • 改变质点的运动状态 质点获得加速度 r F⊥ F// Fn F h F A z
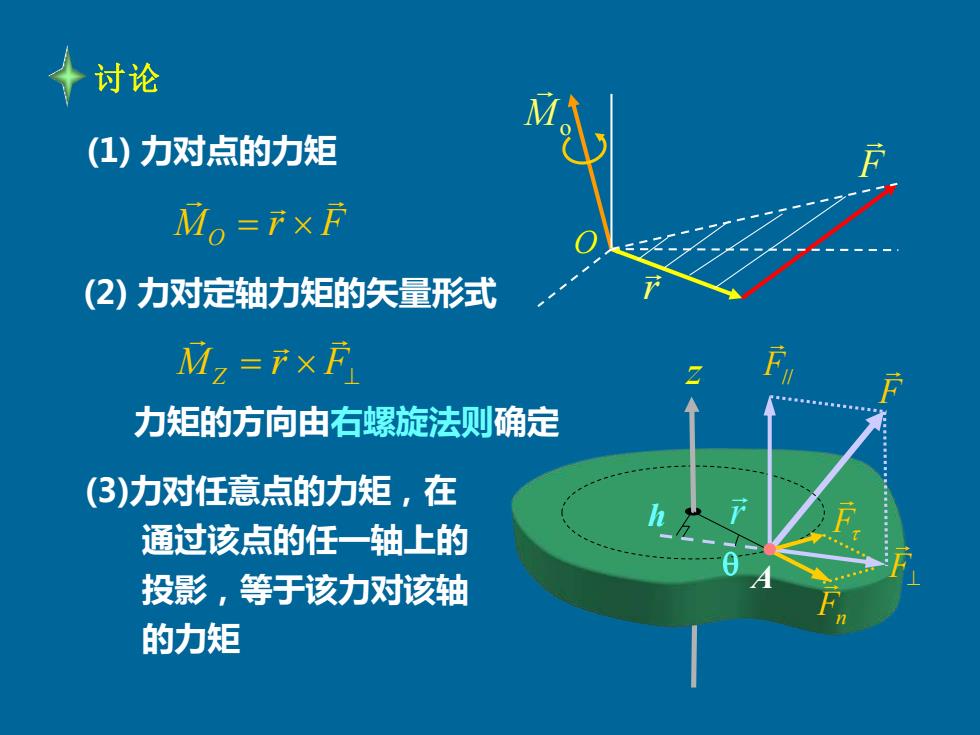
讨论 (1)力对点的力矩 M。=f×F (2)力对定轴力矩的矢量形式 M2=F×F 力矩的方向由右螺旋法则确定 (3)力对任意点的力矩,在 通过该点的任一轴上的 投影,等于该力对该轴 的力矩
(1) 力对点的力矩 O . MO r F = (2) 力对定轴力矩的矢量形式 力矩的方向由右螺旋法则确定 = F⊥ M r Z (3)力对任意点的力矩,在 通过该点的任一轴上的 投影,等于该力对该轴 的力矩 讨论 F r Mo r F⊥ F// Fn F h F A z
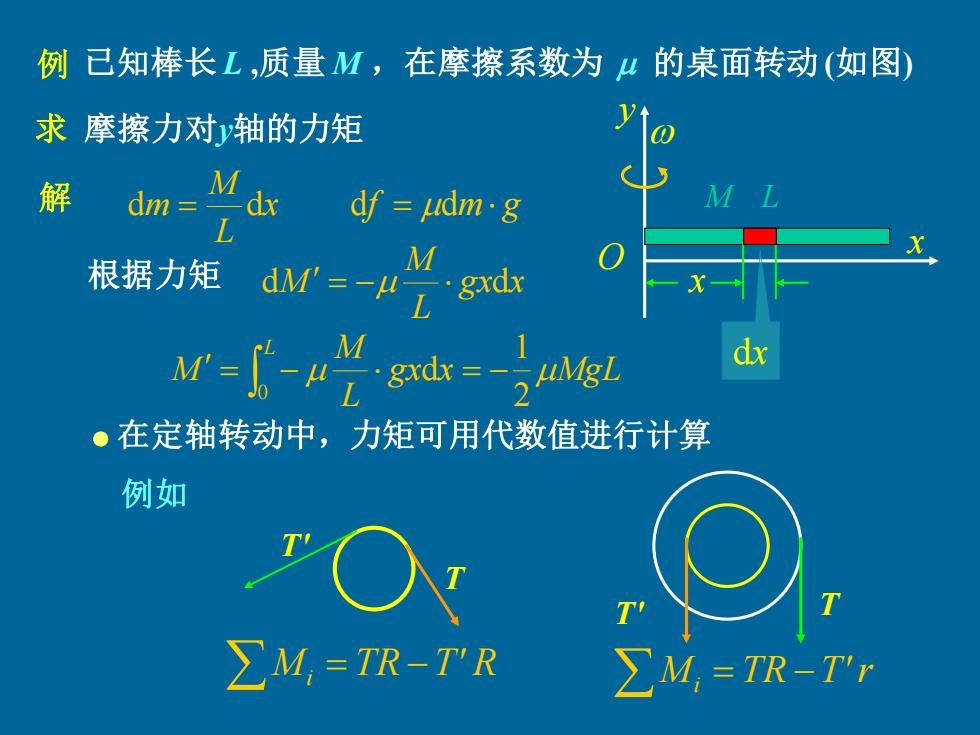
例已知棒长L,质量M,在摩擦系数为u的桌面转动(如图) 求摩擦力对轴的力矩 解 M dm=dx df eudm.g 根据力矩 M dM'=- gxdx dx 。在定轴转动中,力矩可用代数值进行计算 例如 T' ∑M,=TR-T'R ∑M,=TR-T'r
x L O M y 例 已知棒长 L ,质量 M ,在摩擦系数为 的桌面转动(如图) 解 x L M dm = d df = dm g 根据力矩 gx x L M dM = − d gx x MgL L M M L 2 1 d 0 = − = − x dx M TR T'r i = − T' T 例如 T Mi = TR −T' R T' • 在定轴转动中,力矩可用代数值进行计算 求 摩擦力对y轴的力矩
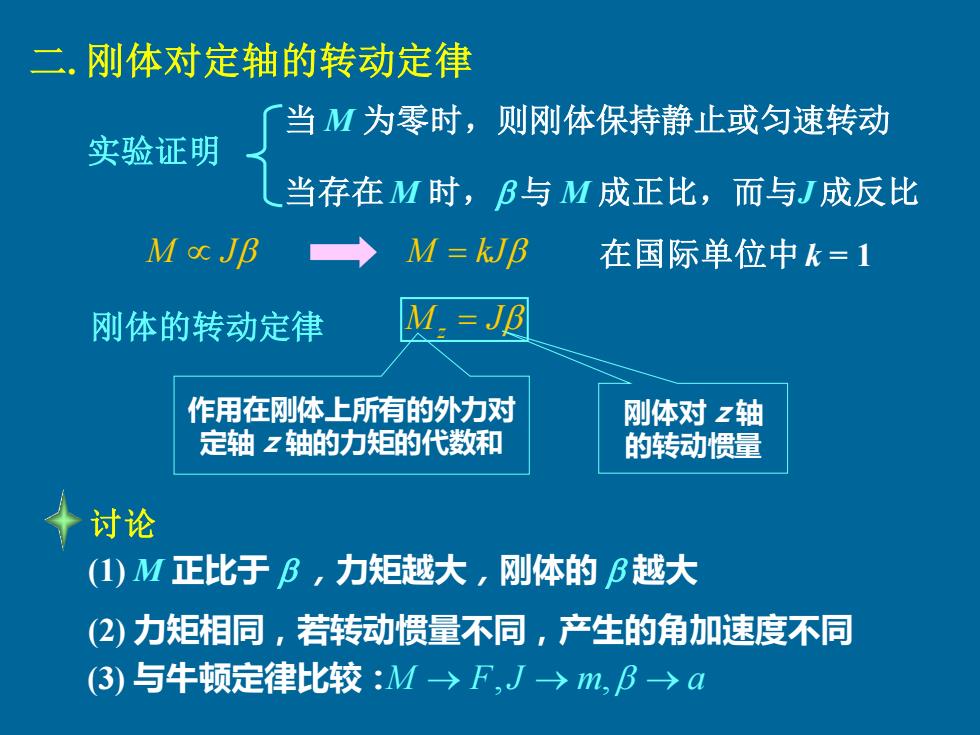
二.刚体对定轴的转动定律 当M为零时,则刚体保持静止或匀速转动 实验证明 当存在M时,B与M成正比,而与J成反比 M∝JB M=kJB 在国际单位中k=1 刚体的转动定律 M.=JB 作用在刚体上所有的外力对 刚体对z轴 定轴Z轴的力矩的代数和 的转动惯量 十讨论 (1)M正比于B,力矩越大,刚体的B越大 (2)力矩相同,若转动惯量不同,产生的角加速度不同 (3)与牛顿定律比较:M→F,J→m,B→@
M J M = kJ 刚体的转动定律 Mz = J 作用在刚体上所有的外力对 定轴 z 轴的力矩的代数和 刚体对 z 轴 的转动惯量 (1) M 正比于 ,力矩越大,刚体的 越大 (2) 力矩相同,若转动惯量不同,产生的角加速度不同 二. 刚体对定轴的转动定律 实验证明 当 M 为零时,则刚体保持静止或匀速转动 当存在 M 时, 与 M 成正比,而与J成反比 (3) 与牛顿定律比较:M → F, J → m, → a 讨论 在国际单位中k = 1

理论推证 取一质量元万+子=m,a 切线方向 Fir+fir=mai 对固定轴的力矩 F+=ma =mB 对所有质元 ∑FH,+∑/,=(∑mp 合外力矩M 合内力矩=0 刚体的转动惯量J
O i r Fi i f • 理论推证 i i miai F f 取一质量元 + = i i i i 切线方向 F + f = m a i i i i i i i F r f r m a r 对固定轴的力矩 + = 2 i i = m r 对所有质元 + = ( ) 2 i i i i i i F r f r m r 合外力矩 M 合内力矩 = 0 刚体的转动惯量J • mi

三.转动惯量 定义式 J=△m, 质量不连续分布 J= r2dm 质量连续分布 ●计算转动惯量的三个要素:(1)总质量(2)质量分布(3)转轴 的位置 (1)J与刚体的总质量有关 例如两根等长的细木棒和细铁棒绕端点轴转动惯量 ML J铁>J木 dx
三. 转动惯量 = 2 i i 定义式 J m r 质量不连续分布 J = r 2 dm 质量连续分布 计算转动惯量的三个要素:(1)总质量(2)质量分布(3)转轴 的位置 (1) J 与刚体的总质量有关 例如两根等长的细木棒和细铁棒绕端点轴转动惯量 L z O x dx 2 M 0 2 0 2 3 1 d dx ML L M J x x x L L = = = J铁 J木 •
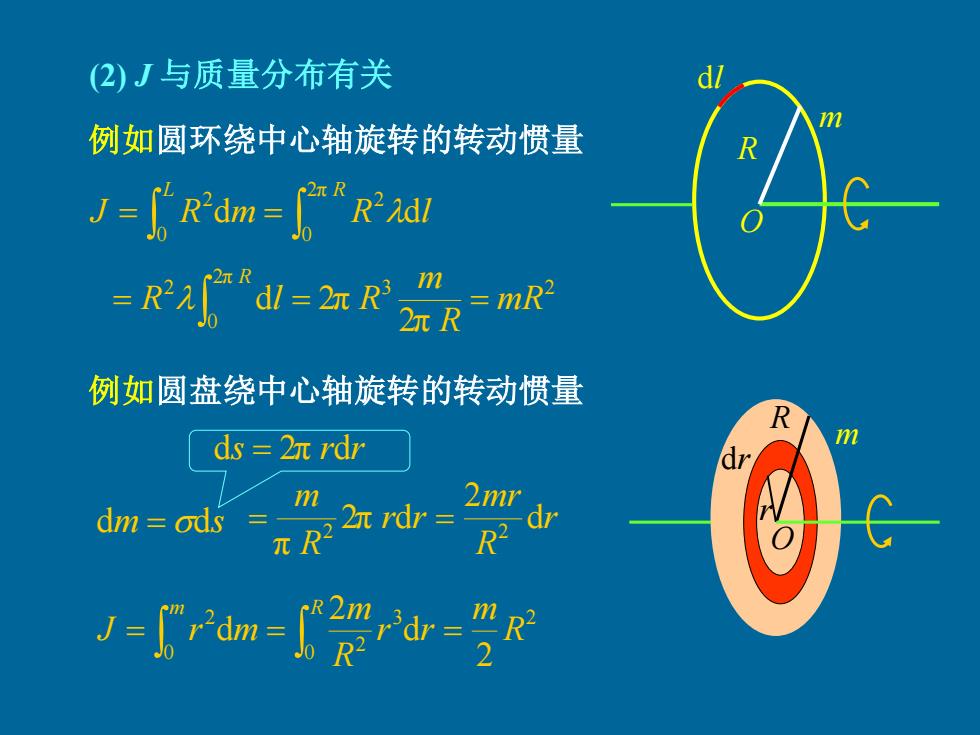
(2)J与质量分布有关 例如圆环绕中心轴旋转的转动惯量 JR'dm=R'ndl =Rd-2 m =mR2 例如圆盘绕中心轴旋转的转动惯量 ds 2n rdr m 2n rdr= 2m dm ods 三 x R2 J=r7dm=20
(2) J 与质量分布有关 例如圆环绕中心轴旋转的转动惯量 例如圆盘绕中心轴旋转的转动惯量 dl = = O L R J R m R l 2π 0 2 0 2 d d 3 2 2π 0 2 2π d 2π mR R m R l R R = = = m R O m r dr ds = 2π rdr dm = ds = = = m R R m r r R m J r m 0 3 2 2 0 2 2 d 2 d r R mr r r R m d 2 2π d π 2 2 = = R
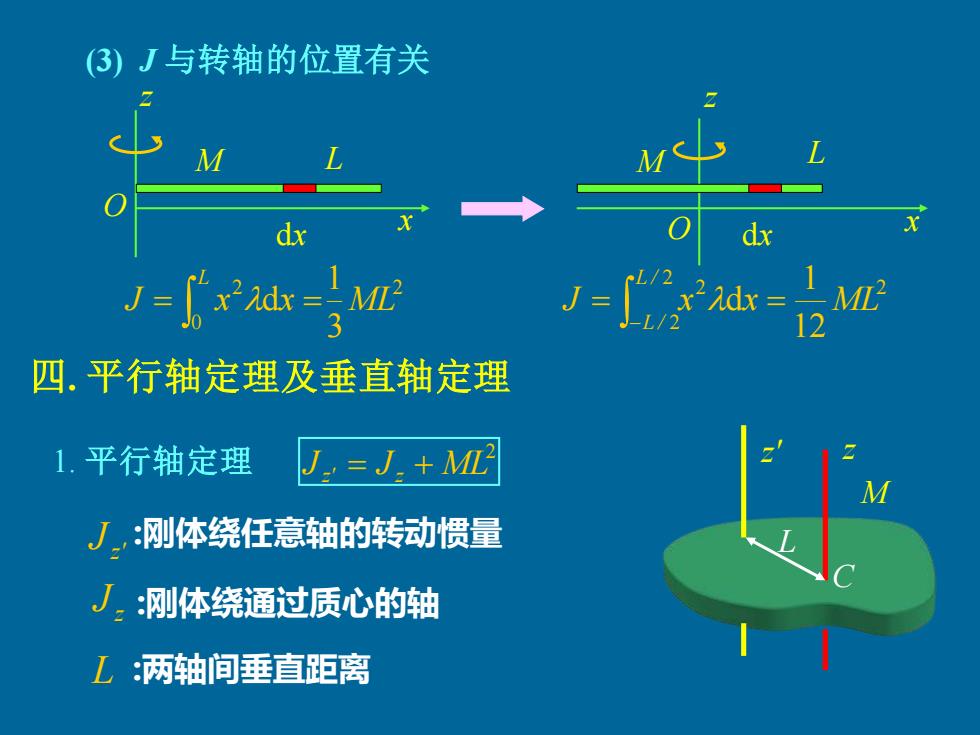
(3)J与转轴的位置有关 d dx [x"Adx =MI 四.平行轴定理及垂直轴定理 1.平行轴定理 J.=J.+ML J.,:刚体绕任意轴的转动惯量 J:刚体绕通过质心的轴 乙:两轴间垂直距离
O L x dx M z 2 0 2 3 1 J x dx ML L = = L O x dx M 2 2 2 2 12 1 J x dx ML L / L / = = − 四. 平行轴定理及垂直轴定理 z L C M ML2 z' J J z' = z + z (3) J 与转轴的位置有关 1. 平行轴定理 z' J z J L :刚体绕任意轴的转动惯量 :刚体绕通过质心的轴 :两轴间垂直距离
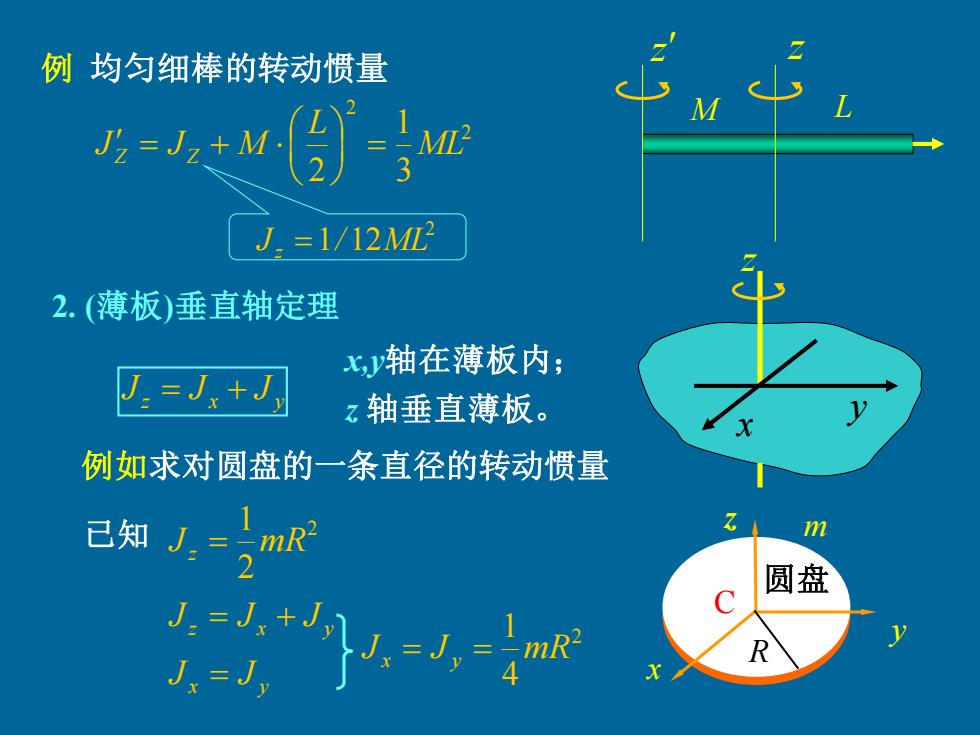
例均匀细棒的转动惯量 J2=Jz+M 2 M J.=1/12M 2.(薄板)垂直轴定理 x,轴在薄板内; J.=J+J z轴垂直薄板。 例如求对圆盘的一条直径的转动惯量 1 已知J=mR m 圆盘 √+山,=JmR R J=J
2 Jz =1/ 12ML 2 2 3 1 2 ML L JZ JZ M = = + 例 均匀细棒的转动惯量 2. (薄板)垂直轴定理 z x y J = J + J z M L z 例如求对圆盘的一条直径的转动惯量 2 2 1 Jz = mR z x y J = J + J x y J = J 已知 2 4 1 Jx = J y = mR y x z 圆盘 R C m x,y轴在薄板内; z 轴垂直薄板。 z x y