
第1章质点运动学 国家激光波长基准 National laser wavelength standard 激光波长基准装置
第1章 质点运动学 激光波长基准装置
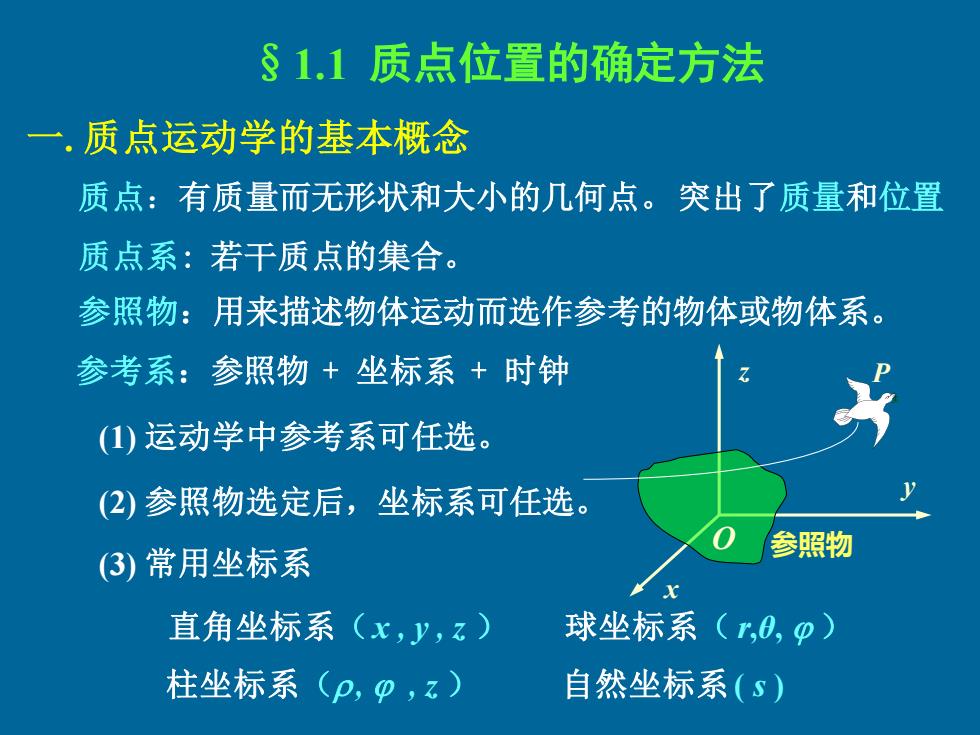
§1,1质点位置的确定方法 一,质点运动学的基本概念 质点:有质量而无形状和大小的几何点。突出了质量和位置 质点系:若干质点的集合。 参照物:用来描述物体运动而选作参考的物体或物体系。 参考系:参照物+坐标系+时钟 (1)运动学中参考系可任选。 (②)参照物选定后,坐标系可任选。 (3)常用坐标系 参照物 直角坐标系(x,y,乙) 球坐标系(r,0,p) 柱坐标系(p,p,z) 自然坐标系(s)
§1.1 质点位置的确定方法 一. 质点运动学的基本概念 质点:有质量而无形状和大小的几何点。突出了质量和位置 质点系: 若干质点的集合。 x y z O 参照物 参考系:参照物 + 坐标系 + 时钟 (1) 运动学中参考系可任选。 参照物:用来描述物体运动而选作参考的物体或物体系。 P (2) 参照物选定后,坐标系可任选。 (3) 常用坐标系 直角坐标系(x , y , z ) 球坐标系( r,θ, ) 柱坐标系( , , z ) 自然坐标系( s )
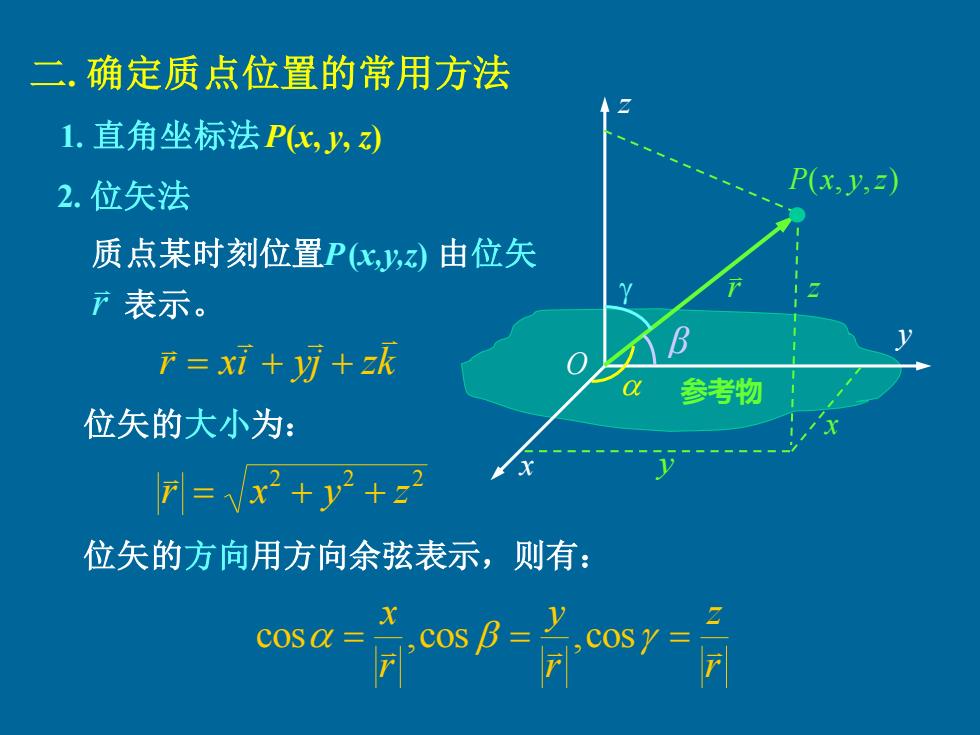
二,确定质点位置的常用方法 1.直角坐标法P,y,) 2.位矢法 P(x,y,) 质点某时刻位置P,z)由位矢 下表示。 r =xi+yj+zk 参考物 位矢的大小为: r=vx2+y2+22 位矢的方向用方向余弦表示,则有: X cosa= cosB=六c0s7=
二. 确定质点位置的常用方法 1. 直角坐标法P(x, y, z) 2. 位矢法 r xi yj zk = + + r 表示。 位矢的大小为: 2 2 2 r = x + y + z 位矢的方向用方向余弦表示,则有: cos ,cos ,cos r z r y r x = = = z x y O z P(x, y,z) y x r β 参考物 质点某时刻位置P (x,y,z) 由位矢
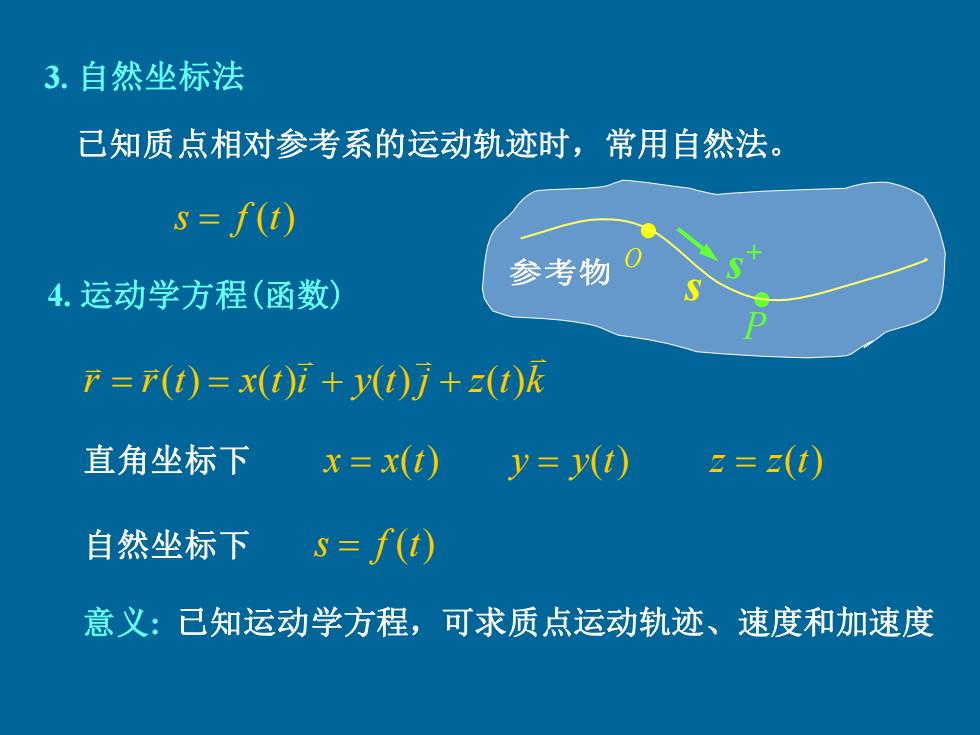
3.自然坐标法 己知质点相对参考系的运动轨迹时,常用自然法。 s=f(t) 参考物 4.运动学方程(函数) r=r(t)=x(t)i+y(t)j+z(t)k 直角坐标下 x=x(t) y=y(t) 2=z(t) 自然坐标下s=f(t) 意义:已知运动学方程,可求质点运动轨迹、速度和加速度
• • 3. 自然坐标法 已知质点相对参考系的运动轨迹时,常用自然法。 4. 运动学方程(函数) 直角坐标下 x = x(t) y = y(t) z = z(t) r r t x t i y t j z t k = ( ) = ( ) + ( ) + ( ) 自然坐标下 s = f (t) 已知运动学方程,可求质点运动轨迹、速度和加速度 参考物 O s P + s s = f (t) 意义:

例一质点作匀速圆周运动,半径为r,角速度为0。 求用直角坐标、位矢、自然坐标表示的质点运动学方程。 解以圆心0为原点。建立直角坐标 系Oxy,O'点为起始时刻,设t时 刻质点位于P(x,y),用直角坐 P(x,y) 标表示的质点运动学方程为 x=rcosot,y=rsin@t 位矢表示为 F=xi +yj rcosoti +rsinoy 自然坐标表示为 s=rot
一质点作匀速圆周运动,半径为r ,角速度为 。 以圆心O 为原点。建立直角坐标 系Oxy ,O 点为起始时刻,设t 时 刻质点位于P(x , y),用直角坐 标表示的质点运动学方程为 x = r cos t, y = rsin t s = rt 位矢表示为 自然坐标表示为 x y P ωt x y O r s 例 解 • (x, y) O' • • r xi yj r ti r tj = + = cos + sin 求 用直角坐标、位矢、自然坐标表示的质点运动学方程
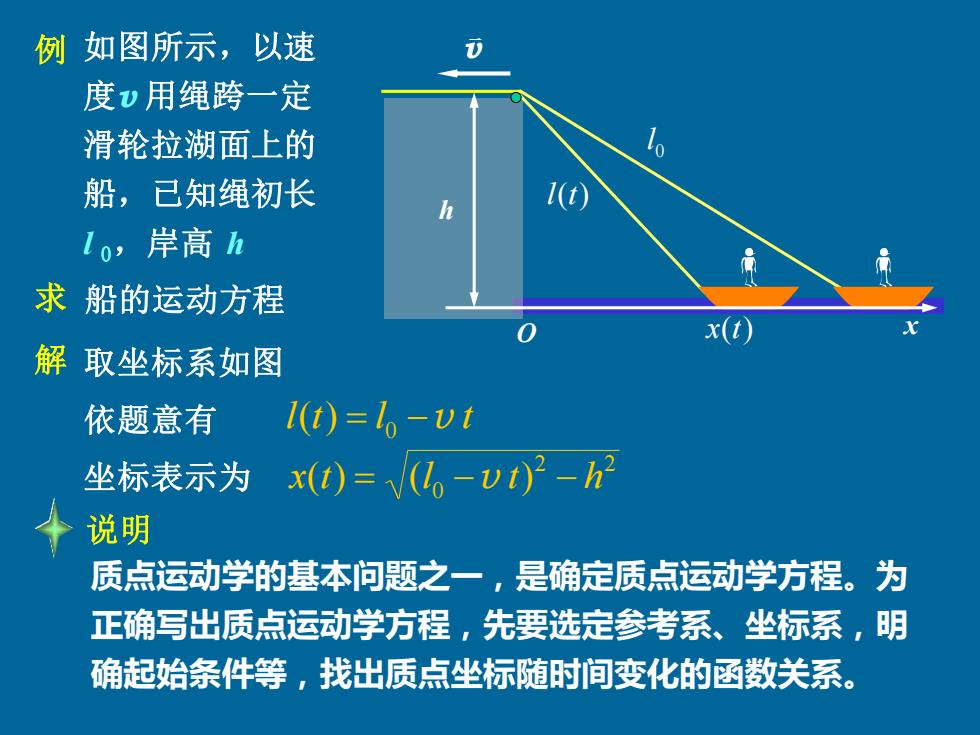
例 如图所示,以速 度v用绳跨一定 滑轮拉湖面上的 船,已知绳初长 10,岸高 求船的运动方程 x(t) 解取坐标系如图 依题意有 1(t)=l。-vt 坐标表示为 x(t)=V(亿。-v}-h ◆说明 质点运动学的基本问题之一,是确定质点运动学方程。为 正确写出质点运动学方程,先要选定参考系、坐标系,明 确起始条件等,找出质点坐标随时间变化的函数关系
求 解 h v x 2 2 0 坐标表示为 x(t) = (l −v t) − h 例 如图所示,以速 度v 用绳跨一定 滑轮拉湖面上的 船,已知绳初长 l 0,岸高 h 取坐标系如图 依题意有 l(t) l t = 0 −v 质点运动学的基本问题之一,是确定质点运动学方程。为 正确写出质点运动学方程,先要选定参考系、坐标系,明 确起始条件等,找出质点坐标随时间变化的函数关系。 0 l l(t) O x(t) 船的运动方程 说明
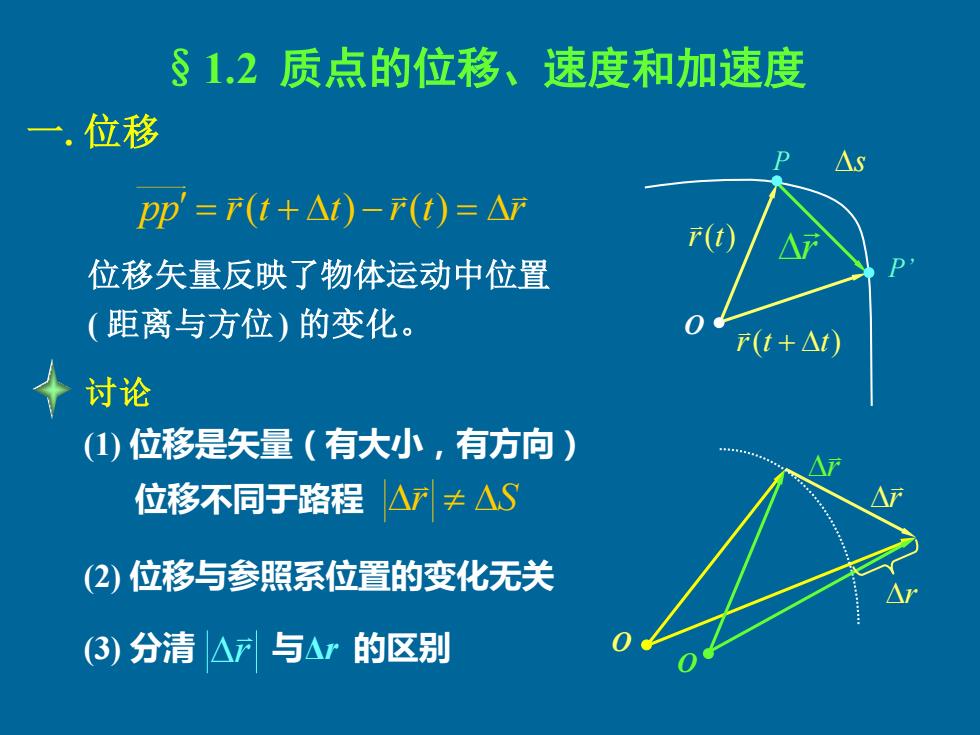
§1.2质点的位移、速度和加速度 一,位移 △S Pp'=T(t+△1)-(t)=W 位移矢量反映了物体运动中位置 (距离与方位)的变化。 F(t+△t) 讨论 (1)位移是矢量(有大小,有方向) 位移不同于路程△7≠△S (2)位移与参照系位置的变化无关 (③)分清△F与△r的区别
§1.2 质点的位移、速度和加速度 一. 位移 位移矢量反映了物体运动中位置 ( 距离与方位) 的变化。 讨论 (1) 位移是矢量(有大小,有方向) 位移不同于路程 (2) 位移与参照系位置的变化无关 pp r t t r t r = ( + ) − ( ) = r S (3) r 与Δr 的区别 O P P’ r r(t) r(t + t) s O r r O r 分清 • • • • •
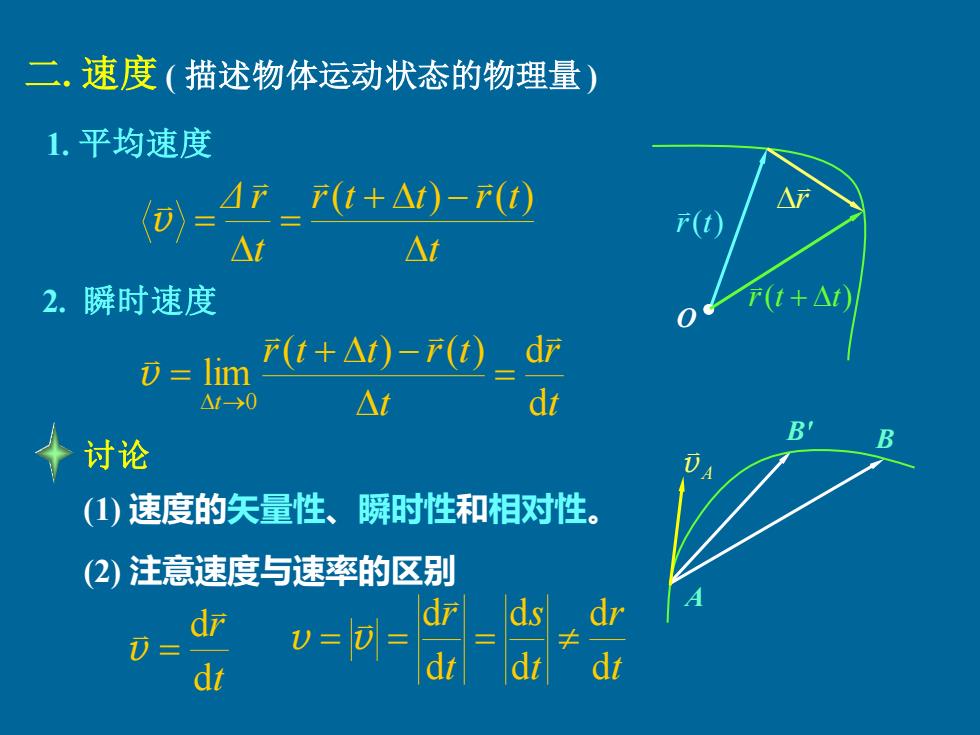
二.速度(描述物体运动状态的物理量) 1.平均速度 (D)=4F=(+A)-F() △ r(t) △t △t 2.瞬时速度 r(t+△t F(t+△)-r(t)d =lim △M-→0 △t di ◆讨论 B B ①》 (1)速度的矢量性、瞬时性和相对性。 (2)注意速度与速率的区别 dr dr ds D= dt dt dt
二. 速度 ( 描述物体运动状态的物理量 ) 1. 平均速度 t r t t r t t Δ r + − = = ( ) ( ) v O r r(t + t) r(t) 2. 瞬时速度 t r t r t t r t t d ( ) ( ) d lim 0 = + − = → v A B' B v A 讨论 (1) 速度的矢量性、瞬时性和相对性。 (2) 注意速度与速率的区别 t r d d v = • t r t s t r d d d d d d = = = v v
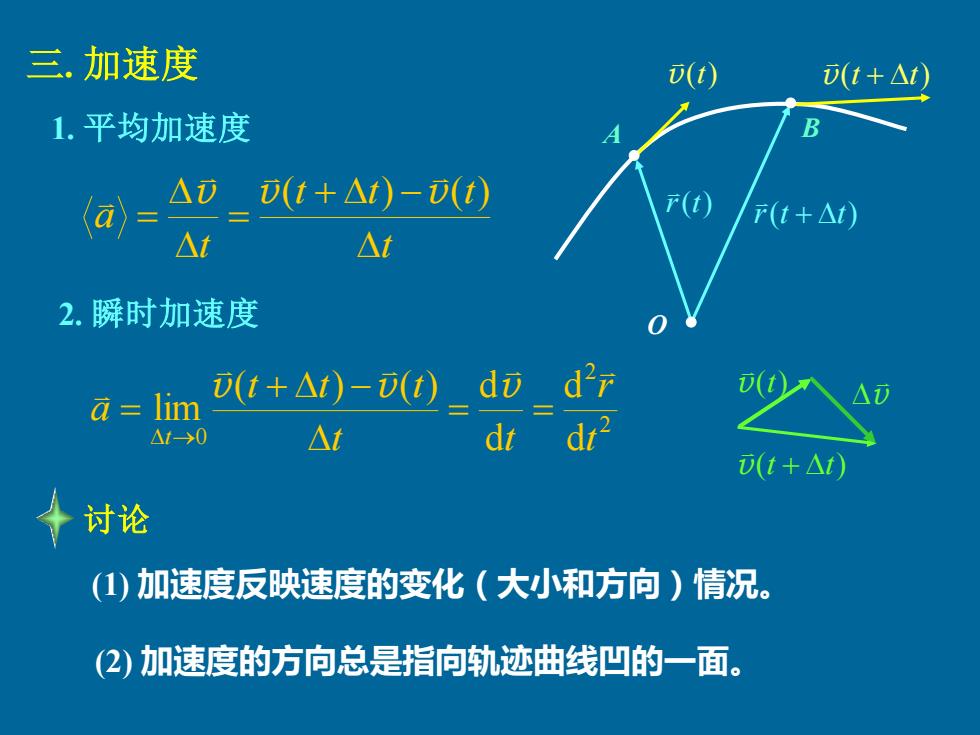
三.加速度 (t) (t+△t) 1.平均加速度 a △边(t+△t)-(t F(t+△t △t △t 2.瞬时加速度 lim v(t+At)-(t)di d2r △10 △t dt D(t+△) ◆讨论 (1)加速度反映速度的变化(大小和方向)情况。 (2)加速度的方向总是指向轨迹曲线凹的一面
三. 加速度 1. 平均加速度 t t t t t a + − = = v v( ) v( ) 2. 瞬时加速度 讨论 (1) 加速度反映速度的变化(大小和方向)情况。 2 2 0 d d d ( ) ( ) d lim t r t t t t t a t = = + − = → v v v v(t) v(t + t) v A B v(t) v(t + t) r(t) r(t + t) O (2) 加速度的方向总是指向轨迹曲线凹的一面。 • • •

§1.3用直角坐标表示位移、速度和加速度 一,位移 时刻t,质点位于P,位矢为 乙P(3,) 时刻t+t,质点位于Q,位矢为 建如图所示坐标,则 方=x7+乃)+2k 2=x,i+y32j+22k (x2,2,22) 时间4t内质点的位移为△=一 △=△xi+△7+△k =(x2-x)+(y2-)7+(三2-)k
§1.3 用直角坐标表示位移、速度和加速度 一. 位移 2 1 r r r = − r xi yj zk = + + x y z O r 1 r 2 r P Q 时刻 t ,质点位于P ,位矢为 1 r 时刻 t +t ,质点位于 Q ,位矢为 2 r r x i y j z k 1 = 1 + 1 + 1 r x i y j z k 2 = 2 + 2 + 2 时间 t 内质点的位移为 x x i y y j z z k ( ) ( ) ( ) = 2 − 1 + 2 − 1 + 2 − 1 ( , , ) 1 1 1 x y z ( , , ) 2 2 2 x y z 建如图所示坐标,则 • • •