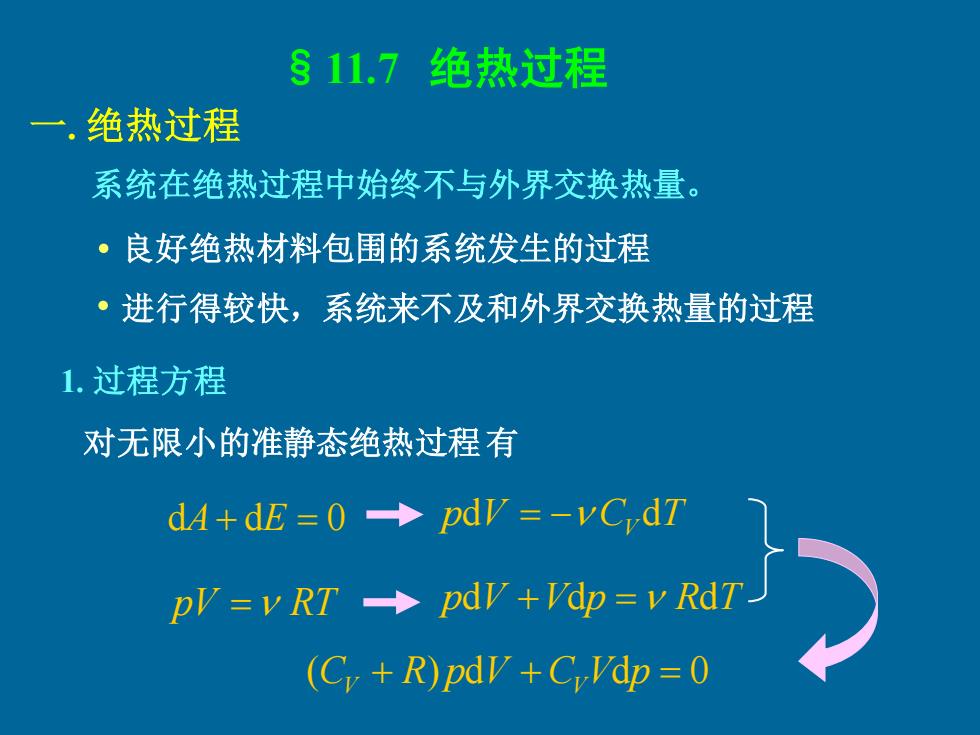
§11.7绝热过程 一,绝热过程 系统在绝热过程中始终不与外界交换热量。 ·良好绝热材料包围的系统发生的过程 ·进行得较快,系统来不及和外界交换热量的过程 1.过程方程 对无限小的准静态绝热过程有 dA+dE=0◆pdV=-vCdT pV=vRT-pdv+Vdp=v RdT (Cy R)pdy+CrVdp=0
§11.7 绝热过程 一. 绝热过程 系统在绝热过程中始终不与外界交换热量。 良好绝热材料包围的系统发生的过程 进行得较快,系统来不及和外界交换热量的过程 1. 过程方程 对无限小的准静态绝热过程有 · · dA+ dE = 0 pdV = − CV dT pV = RT pdV +Vdp = RdT (C + R) pdV + C Vdp = 0 V V
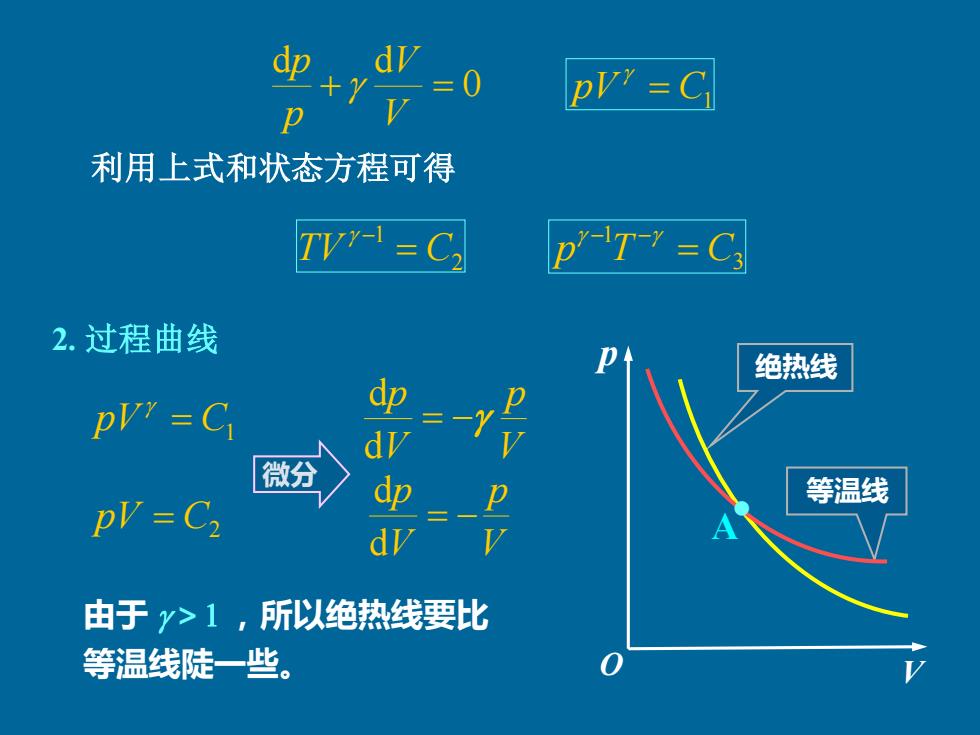
=0 pl7 C p 利用上式和状态方程可得 TV-C, p-T C, 2.过程曲线 绝热线 pVr=C dp d 微分 等温线 pV C dp d 由于y>1,所以绝热线要比 等温线陡一些
0 d d + = V V p p pV = C1 2 1 TV = C − 3 1 p T = C − − 利用上式和状态方程可得 2. 过程曲线 V p V p = − d d pV = C2 C1 pV = V p V p = − d d 微分 A 绝热线 等温线 由于 >1 ,所以绝热线要比 等温线陡一些。 • V p O

3.绝热过程中功的计算 A=-(E2-E)=-vC(T3-I) A=r=所p=,-p》 绝热过程中,理想气体不吸收热量,系统减少的内能,等 于其对外作功
绝热过程中 ,理想气体不吸收热量,系统减少的内能,等 于其对外作功 。 = = 2 1 2 1 d d 1 1 V V V V V V A p V pV ( ) 1 1 p1V1 − p2V2 − = 3. 绝热过程中功的计算 ( ) A = − E2 − E1 ( ) = − CV T2 −T1

例一定量氮气,其初始温度为300K,压强为1atm。将其绝热 压缩,使其体积变为初始体积的1/5。 求压缩后的压强和温度 解氮气是双原子分子 (7/5)7 C (5/2)5 根据绝热过程方程的p、V关系,有 7 p2=p,(W/W2)Y=1x55=9.52atm 根据绝热过程方程的T、V关系,有 T=T(W/VY=300×55=571K
一定量氮气,其初始温度为300K,压强为1atm。将其绝热 压缩,使其体积变为初始体积的1/5。 解 例 求 压缩后的压强和温度 ( ) 1 5 5 9.52atm 7 2 = 1 1 2 = = p p V V ( ) 300 5 571K 1 5 7 1 2 = 1 1 2 = = − − T T V V 5 7 (5 2) (7 5) = = = V p C C 根据绝热过程方程的p﹑V 关系,有 根据绝热过程方程的T﹑V 关系,有 氮气是双原子分子
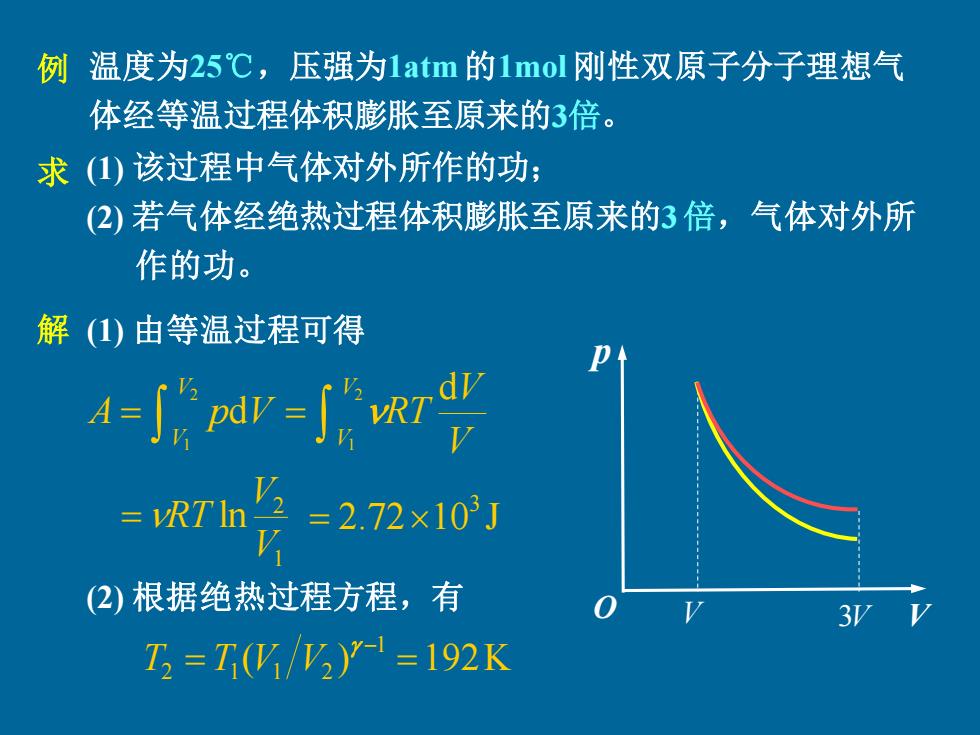
例温度为25℃,压强为1atm的1mol刚性双原子分子理想气 体经等温过程体积膨胀至原来的3倍。 求()该过程中气体对外所作的功: (2)若气体经绝热过程体积膨胀至原来的3倍,气体对外所 作的功。 解(1)由等温过程可得 =r- =R71n=2.72×10J 2)根据绝热过程方程,有 37 T3=T(V/)Y1=192K
温度为25℃,压强为1atm 的1mol 刚性双原子分子理想气 体经等温过程体积膨胀至原来的3倍。 (1) 该过程中气体对外所作的功; (2) 若气体经绝热过程体积膨胀至原来的3 倍,气体对外所 作的功。 解 例 求 V p O V 3V = = 2 1 2 1 d d V V V V V V A p V RT 1 2 ln V V =RT (1) 由等温过程可得 2.72 10 J 3 = (2) 根据绝热过程方程,有 ( ) 192K 1 2 = 1 1 2 = − T T V V

将热力学第一定律应用于绝热过程方程中,有 A=-AE AE=C(T,-T)=-2.2×103j A=2.2×103J
( ) E =CV T2 −T1 2.2 10 J 3 = − 2.2 10 J 3 A = 将热力学第一定律应用于绝热过程方程中,有 A = −E
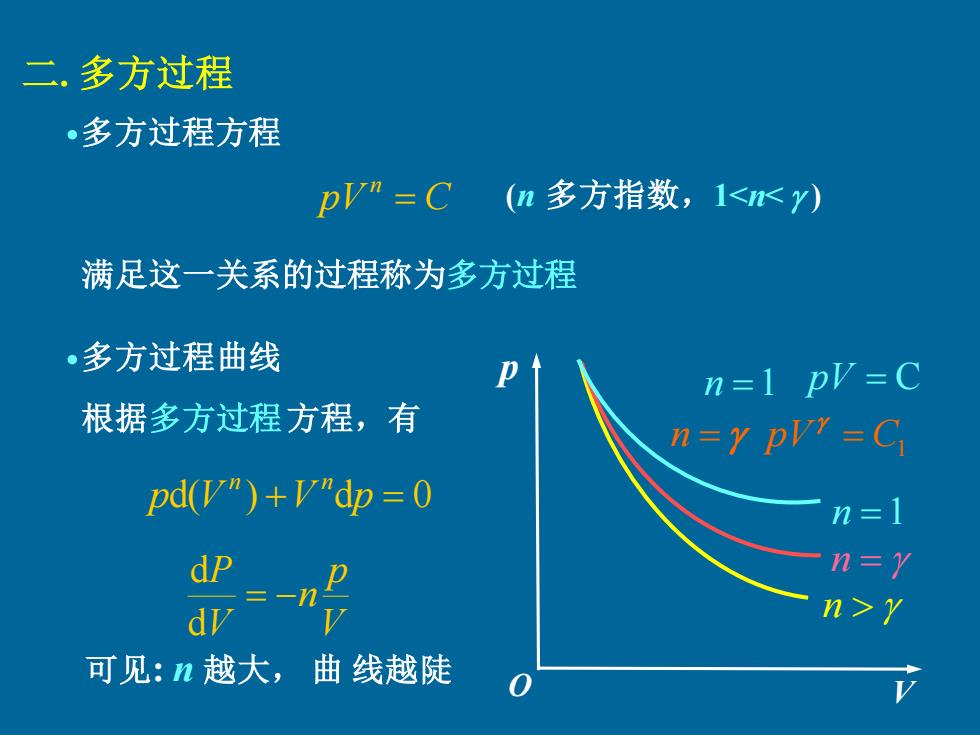
二,多方过程 多方过程方程 pVm=C(n多方指数,1Y 可见:n越大,曲线越陡
二. 多方过程 pV C n = 满足这一关系的过程称为多方过程 (n 多方指数,1<n< ) n = n =1 pV = C pV = C1 n n =1 n = V p n V P = − d d pd(V ) +V dp = 0 n n 可见: n 越大, 曲 线越陡 根据多方过程方程,有 V p O ·多方过程方程 ·多方过程曲线

多方过程中的功、内能、热量、摩尔热容的计算 功4=r-jn=nr-p n-) R 内能增量 △E=C(T,-T) 热量 en=vC (T2-T)=AE+A 摩尔热容 .=C(I-I)+R △T T-T 1-n R =C+ 1-n n-1
功 = = 2 1 2 1 d d 1 1 V V n n V V V V A p V pV ( ) 1 1 p1V1 p2V2 n − − = ( ) 1 T2 T1 n R − − = − ( ) 内能增量 E =CV T2 −T1 热量 Qn =Cn (T2 −T1 ) = E + A 摩尔热容 ·多方过程中的功﹑内能﹑热量﹑摩尔热容的计算 V CV n n n R C 1 −1 − = − = + n R T T C T T T Q C n V n − + − − = = 1 ( ) 2 1 2 1
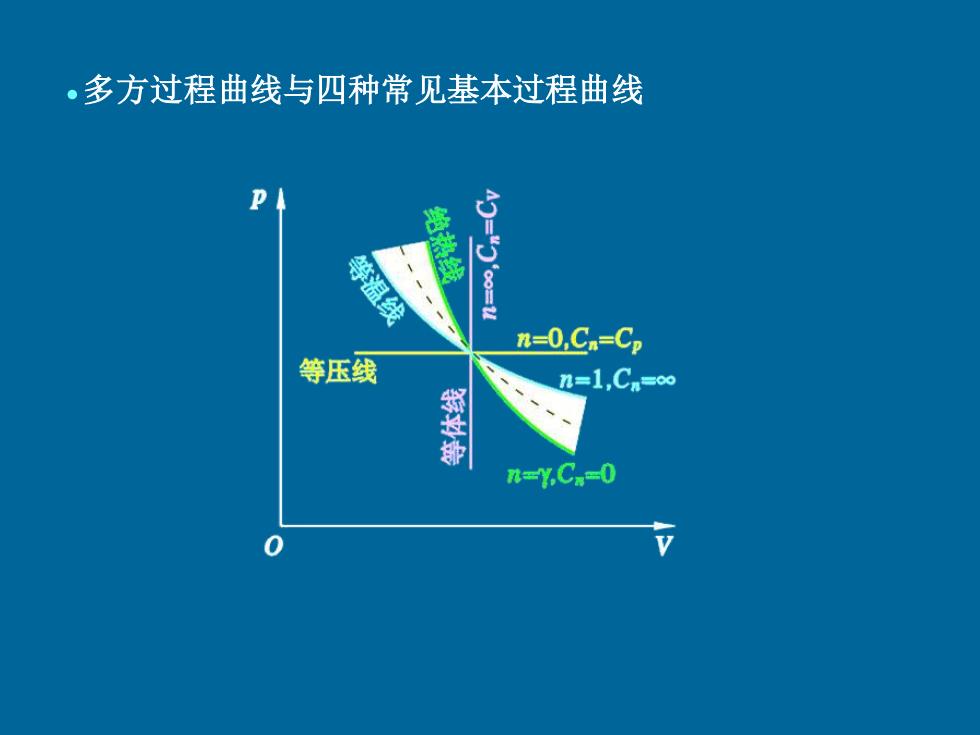
。多方过程曲线与四种常见基本过程曲线 等温线 n=0,Cn=Cp 等压线 n=1,Cn=0o n=YC.=0
·多方过程曲线与四种常见基本过程曲线
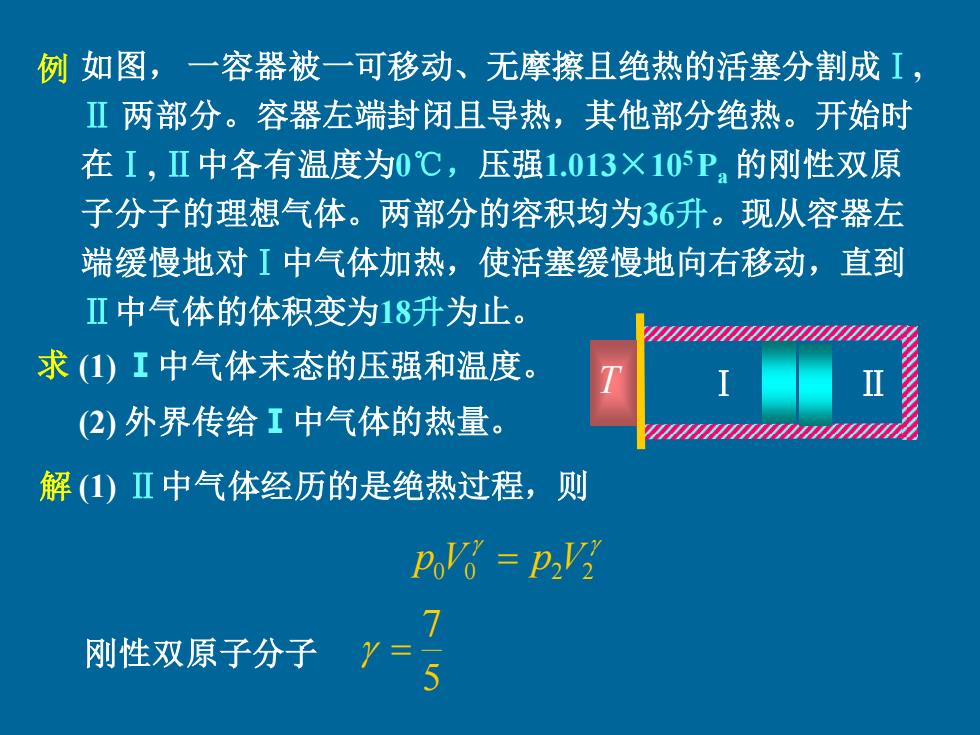
例如图,一容器被一可移动、无摩擦且绝热的活塞分割成I Ⅱ两部分。容器左端封闭且导热,其他部分绝热。开始时 在I,Ⅱ中各有温度为0℃,压强1.013×105P,的刚性双原 子分子的理想气体。两部分的容积均为36升。现从容器左 端缓慢地对I中气体加热,使活塞缓慢地向右移动,直到 Ⅱ中气体的体积变为18升为止。 求(1)工中气体末态的压强和温度。 (2)外界传给工中气体的热量。 解(1)Ⅱ中气体经历的是绝热过程,则 PoVo=P2V2 刚性双原子分子 y5
如图, 一容器被一可移动、无摩擦且绝热的活塞分割成Ⅰ, Ⅱ 两部分。容器左端封闭且导热,其他部分绝热。开始时 在Ⅰ, Ⅱ中各有温度为0℃,压强1.013×105 Pa 的刚性双原 子分子的理想气体。两部分的容积均为36升。现从容器左 端缓慢地对Ⅰ中气体加热,使活塞缓慢地向右移动,直到 Ⅱ中气体的体积变为18升为止。 (1) Ⅰ中气体末态的压强和温度。 解 例 求 Ⅰ Ⅱ (1) Ⅱ中气体经历的是绝热过程,则 0 0 2V2 p V = p 5 7 = (2) 外界传给Ⅰ中气体的热量。 T 刚性双原子分子