
第10变化的做场和变化的电场 M.法拉第(1791~1869)伟大的物理学家、化学家、19世纪最伟大的 实验大师。右图为法拉第用过的螺绕环
第10章 变化的磁场和变化的电场 M.法拉第(1791~1869)伟大的物理学家、化学家、19世纪最伟大的 实验大师。右图为法拉第用过的螺绕环
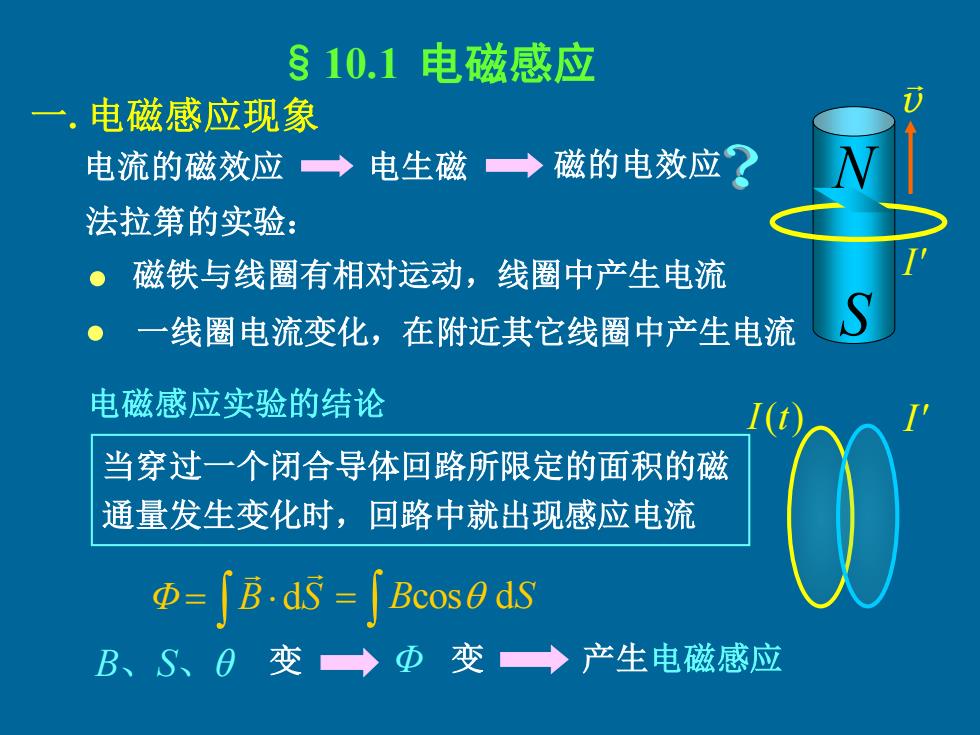
§10.1电磁感应 一.电磁感应现象 电流的磁效应→电生磁→磁的电效应 法拉第的实验: ●磁铁与线圈有相对运动,线圈中产生电流 一线圈电流变化,在附近其它线圈中产生电流 电磁感应实验的结论 I(t 当穿过一个闭合导体回路所限定的面积的磁 通量发生变化时,回路中就出现感应电流 D=「B.dS=Bcos0dS B、S、日变 ◆Φ变→产生电磁感应
电流的磁效应 电生磁 磁的电效应 §10.1 电磁感应 法拉第的实验: 磁铁与线圈有相对运动,线圈中产生电流 N 一线圈电流变化,在附近其它线圈中产生电流 S 电磁感应实验的结论 当穿过一个闭合导体回路所限定的面积的磁 通量发生变化时,回路中就出现感应电流 Φ= B S d = Bcos dS v B、S、θ 变 Φ 变 产生电磁感应I(t) I' I' 一. 电磁感应现象 • •
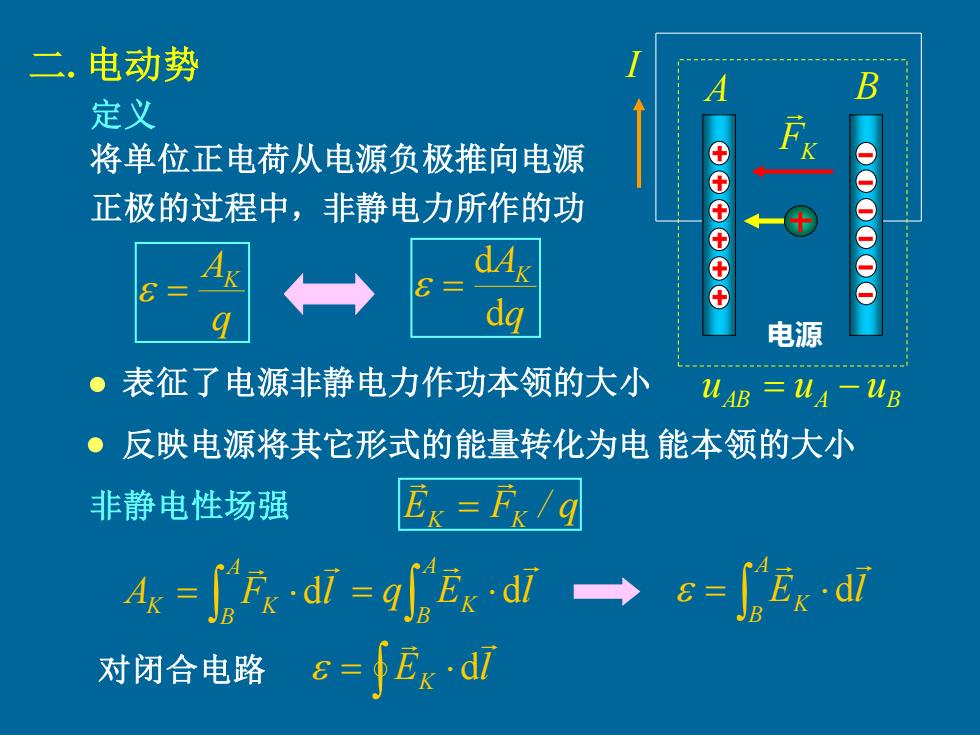
二.电动势 B 定义 将单位正电荷从电源负极推向电源 正极的过程中,非静电力所作的功 ++++++ 一十 电源 。表征了电源非静电力作功本领的大小 U4B=UA一MB ·反映电源将其它形式的能量转化为电能本领的大小 非静电性场强 Ex=Fk/q 4w=Fdl=9Eedi→8=Exdl 对闭合电路 =Ek.di
二. 电动势 A B AB A B u = u − u I 电源 FK 将单位正电荷从电源负极推向电源 正极的过程中,非静电力所作的功 定义 q AK = q AK d d = 表征了电源非静电力作功本领的大小 反映电源将其它形式的能量转化为电 能本领的大小 非静电性场强 EK FK / q = = A B K K A F l d = A B K q E l d = A B K E l d • • 对闭合电路 = E l K d

三.电磁感应定律 ●法拉第的实验规律 感应电动势的大小与通过导体 dΦ 回路的磁通量的变化率成正比 dt 负号表示感应电流的效果总是反抗引起感应电流的原因 楞次定律 n↑Φ>0 ①>0 Φ0 0 8>0 8<0
三. 电磁感应定律 法拉第的实验规律 感应电动势的大小与通过导体 回路的磁通量的变化率成正比 t Φ d d = − 负号表示感应电流的效果总是反抗引起感应电流的原因 —— 楞次定律 0 d d t Φ n n n n 0 d d t Φ 0 d d t Φ 0 d d t Φ N S N N N S S S Φ 0 Φ 0 Φ 0 Φ 0 0 0 0 0 •

讨论 (1)若回路是N匝密绕线圈£=一 dΦ dNΦ d平 dt dt dt dΦ (2)若闭合回路中电阻为R →1,= dqi R Rdt 感应电荷9=1=-人d办=-)/R 例匀强磁场中,导线可在导轨上滑动, 求回路中感应电动势。 B 解在t时刻t)=Bls(t) s(t) dΦ Blds 8三一 =-Blv dt dt 若 6=_ dΦ B=B(t)=Bot =-(Bols Botlv) dt
(1) 若回路是 N 匝密绕线圈 t Φ N d d = − t NΦ d d( ) = − t Ψ d d = − (2) 若闭合回路中电阻为R R t Φ R I i d d = = − t qi d d = 感应电荷 = 2 1 d t t i i q I t = − 2 1 d Φ 1 Φ Φ R = (Φ1 −Φ2 )/ R 讨论 例 匀强磁场中,导线可在导轨上滑动, l v B 解 s(t) Φ(t) = Bls(t) t Φ d d = − Blv t Bl s = − = − d d 在 t 时刻 a b 求 回路中感应电动势。 若 B B t B t 0 = ( ) = t Φ d d = − ( ) = − B0 ls + B0 tlv
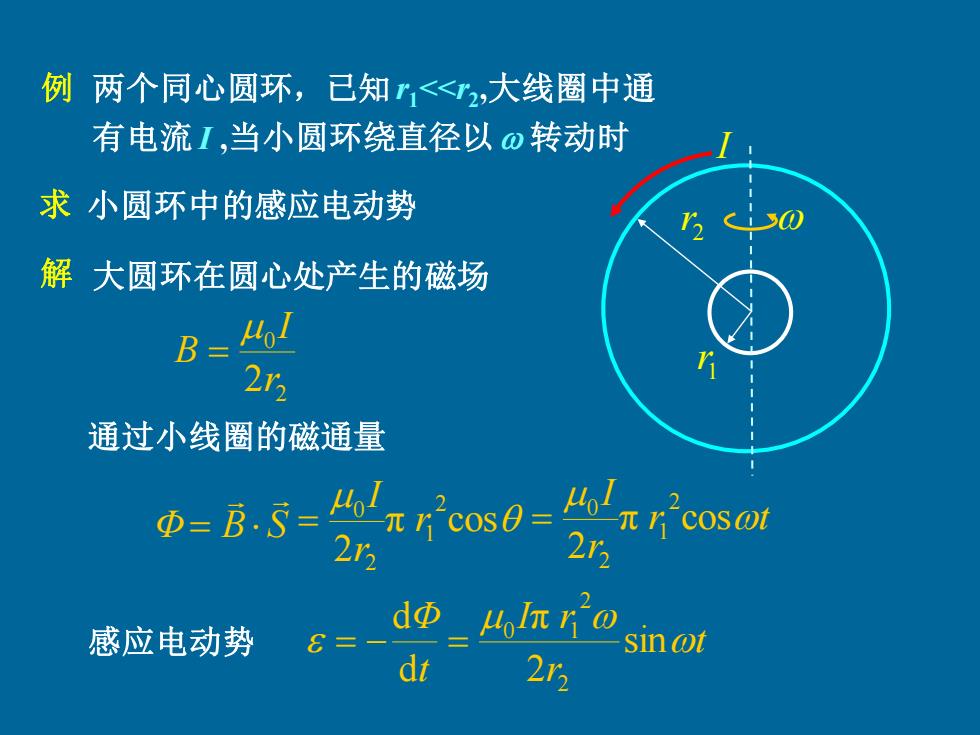
例两个同心圆环,已知r,<2,大线圈中通 有电流I,当小圆环绕直径以o转动时 求小圆环中的感应电动势 解大圆环在圆心处产生的磁场 B= 2r2 通过小线圈的磁通量 D=B.5=H 元cos0='元osan 2r5 21 2 感应电动势 6、 dΦ sin @t dt 2r2
两个同心圆环,已知r1<<r2 ,大线圈中通 有电流 I ,当小圆环绕直径以 转动时 2 r 1 r I 解 2 0 2r I B = 大圆环在圆心处产生的磁场 通过小线圈的磁通量 Φ B S = π cos 2 2 1 2 0 r r I = r t r I π cos 2 2 1 2 0 = t r I r t Φ sin 2 π d d 2 2 0 1 = − = 例 感应电动势 求 小圆环中的感应电动势
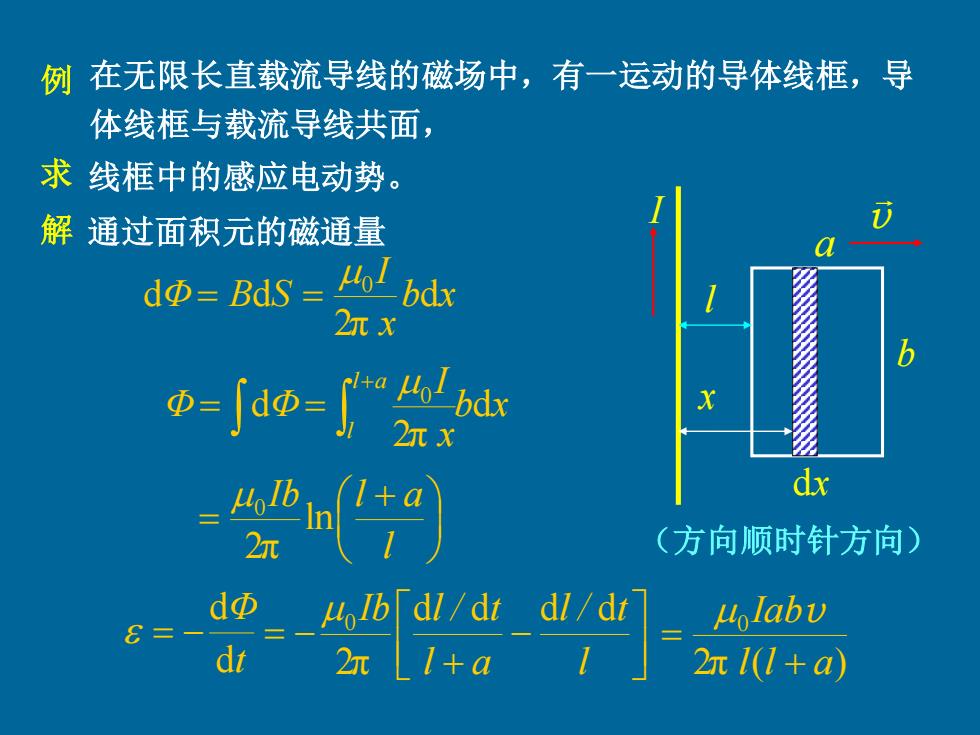
例在无限长直载流导线的磁场中,有一运动的导体线框,导 体线框与载流导线共面, 求线框中的感应电动势。 解通过面积元的磁通量 dΦ=Bds=,/bdk 2n x dx 2元 (方向顺时针方向) dΦ olbdl/dt dl/dt Lolabv dt t l+a 2 2r1(1+a)
在无限长直载流导线的磁场中,有一运动的导体线框,导 体线框与载流导线共面, I v a b dx x 解 b x x I Φ B S d 2π d d 0 = = 通过面积元的磁通量 b x x I Φ Φ l a l d 2π d 0 + = = + = l Ib l a ln 2π 0 t Φ d d = − l − + = − l l / t l a Ib dl / dt d d 2π 0 2π ( ) 0 l l a Iab + = v (方向顺时针方向) 例 求 线框中的感应电动势
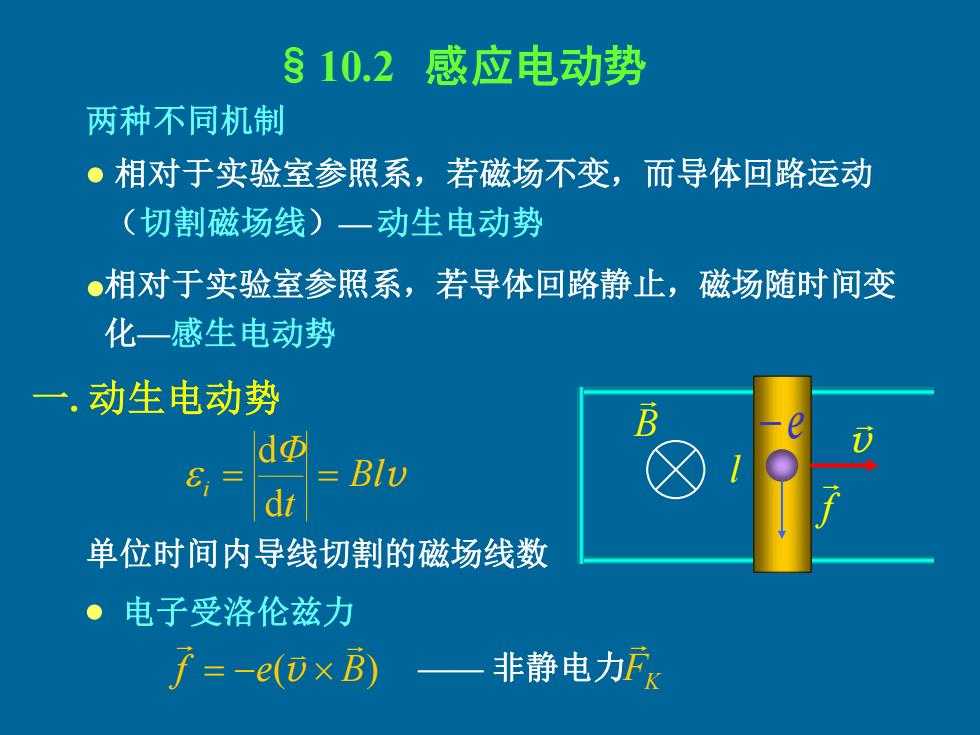
§10.2感应电动势 两种不同机制 。相对于实验室参照系,若磁场不变,而导体回路运动 (切割磁场线)一动生电动势 ●相对于实验室参照系,若导体回路静止,磁场随时间变 化一感生电动势 一,动生电动势 B dΦ Blv 单位时间内导线切割的磁场线数 ●电子受洛伦兹力 f=-e(UxB) 非静电力F风
§10.2 感应电动势 两种不同机制 相对于实验室参照系,若磁场不变,而导体回路运动 (切割磁场线)—动生电动势 相对于实验室参照系,若导体回路静止,磁场随时间变 化—感生电动势 一. 动生电动势 B l v f 单位时间内导线切割的磁场线数 f e( B) = − v 电子受洛伦兹力 —— 非静电力FK −e Blv t Φ i = = d d • • •

·非静电场 Ek- k=D×B -e 。动生电动势 e,=[Ex-dl =[(ox B)-dT 应用 &=(o×B)-d B ["uBdl vBi 磁场中的运动导线成为电源,非静电力是洛伦兹力
非静电场 e F E K K − = B =v 动生电动势 应用 l d 磁场中的运动导线成为电源,非静电力是洛伦兹力 v l B a b + − = E l i K d + − = B l (v ) d + − = B l i (v ) d B l a b d = v =vBl • •

十讨论 ()注意矢量之间的关系 i×B=0 D×B≠0 (⑦xB).d7=0 d7 (2)对于运动导线回路,电动势存在于整个回路 e=f0×Bd=∫B.(⑦×d) =-fB.(t×dy△t =-「B.dSy△t=一△D/△t(法拉第电磁感应定律)
讨论 (1) 注意矢量之间的关系 v B l d v B (2) 对于运动导线回路,电动势存在于整个回路 i = 0 B = 0 v B 0 v ( B) dl = 0 v = B l i (v ) d ( d ) = − B l v B ( Δt dl )/Δt = − v = − B S t d '/ = −Φ/ t l d (法拉第电磁感应定律)